Индицирование рентгенограмм в случае средних сингоний.
Если вещество кристаллизуется в средней сингонии, учитывается, что величины Q зоны hk0 образуют ряды, подобные использованным при индицировании рентгенограмм кубических кристаллов.
Для тетрагональной сингонии
Qhk0 = A(h2 + k2)
Для гексагональной сингонии
Qhk0 = A(h2 + k2 + hk)
Только часть Q относится к зоне hk0, поэтому первым членом ряда может быть Q2, Q3 и т.д. остальные члены ряда (или часть их) должны получаться при умножении Qh1k10 на числа ряда (h2 + k2) или (h2 + k2 + hk). Если удается найти группу Qn1 для которой справедливо то или иное соотношение, то можно сделать вывод о принадлежности вещества к тетрагональной или гексагональной сингониям. Соотношения типа Qn : Qm = n12 : n22, должны иметь место в любой сингонии. Ряды Q, соответствующие ряду квадратов целых чисел могут использоваться для уточнения небольших Qhkl, так как относительная ошибка в величинах Q уменьшается с увеличением Q. Индексы h1, k1, …, hn, kn при этом остаются не вполне определенными (т.к. неизвестны h1k1). Линии с индексами (100), запрещены во многих пространственных группах. Поэтому после выделения ряда hk0, целесообразно проверить, все hk0, т.е. нельзя ли найти дополнительные члены ряда, если в качестве первого члена взять не Qh1k1, а Qh1k1/N, где N = h2 + k2 или h2 + k2 + hk, в зависимости от сингонии.
Достаточно ограничиться N = 2(3) и 4 (т.е. приписать индексы 110 и 200). Отсутствие дополнительных членов ряда hk0 не вносят окончательной ясности в значение h1k1: в тетрагональной сингонии могут быть запрещены линии hk0 с h + k 2n, а для гексагональной - с индексами h– k 3n. Эту неоднозначность следует иметь ввиду при индицировании соответствующих рентгенограмм.
Оставшиеся величины должны иметь индексы
hkl (в т.ч. и 00l).
Среди них можно выделить ряды типа
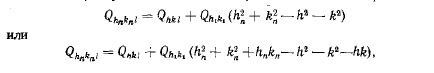
включающие Qhkl с одинаковым индексом l. Рассмотрение коэффициентов при Qhk позволяет уточнить индексы h1k1.
В качестве примера рассмотрим выбор между примитивной и ОЦК – ячейкой в тетрагональной сингонии.
Если ячейка примитивная, то коэффициентами
при Qhk
будут разности
,
если ячейка ОЦК
.
Эти ряды различаются если
.
В частности различны ряды
и
которые
представляют наибольший интерес. В
случае гексагональной сингонии
целесообразно представить ряды
и
.
В результате сопоставления для индексов
можно сделать выбор индексов h1k1
и определить индексы hk
линии hkl.
Аналитический метод индицирования рентгенограмм ромбических кристаллов (метод Хесса - Липсона).
Квадратичная формула для ромбической сингонии имеет вид:
или
(
и т.д.)
Отсюда
,
из этого следует, что
.
В основе метода Хесса – Липсона лежит предположение, что среди разностей sin2 наиболее часто будут встречаться разности, соответствующие Ah2, Bk2, Cl2. Если найти sin2 (ограничиться при этом значении sin2, меньшим какой-либо величины, например 0,1 – 0,2) и выберем из них повторяющиеся наиболее часто, то вероятно, что эти значения будут соответствовать A, B и C, увеличенным в n2 раз. Величины sin2 удобно изображать в виде столбиковой диаграммы. Если разности встречаются повторно, то высота отрезков увеличивается.