Критерии правильности индицирования рентгенограмм.

1. Отношение числа теоретически возможных линий на рентгенограмме к числу обнаруженных экспериментально, должно быть близко к 1. При таком подходе учитываются сисематические погасания.

2. В ходе расшифровки должно наблюдаться хорошее соответствие между экспериментальным и вычисленным значением плотности (т.е. число формульных единиц, приходящихся на элементарную ячейку, может быть близко к целому числу, обычно небольшому). При этом можно учесть, минимальную кратность пространственной группы. Число формульных единиц расчитывается по уравнению

Эмпирический критерий правильности параметра индицирования Де-Вольфа определяется по уравнению

,

где - значение для 20-й линии на рентгенограмме,

- число теоретически возможных линий с < ,

- среднее расхождение между значениями вычисленными и экспериментальными. Индицирование корректно, если < 10.

Помимо формулы критерия правильности Де-Вольфа, широко применима формула Смита – Снайдера

,

где N – число видимых линий,

N_poss – число возможных линий,

F_N – фактор качества,

|2| -среднее отклонение 2 (зависит от качества съемки).

Обратная решетка.

Совокупность узлов, задаваемых векторами, величины которых равны межплоскостным расстояниям, а направления совпадают с направлениями нормалей к данному семейству плоскостей, образуют новую пространственную решетку, которая будет обратной решеткой по отношению к исходной. Если исходная решетка построена на векторах a, b и c, то обратная решетка будет построена на векторах a^, b^, c^, перпендикулярных координатным плоскостям и равных по величине , где - соответствующее межплоскостное расстояние. Объем элементарной ячейки V^ равен обратной величине объема ячейки исходной решетки. Индексы узлов обратной решетки равны индексам плоскостей в прямой решетке. Соотношения между векторами прямой и обратной решеток следующие:

1. Скалярные произведения одноименных векторов равны 1, а разноименных векторов и т.д. 0.

2. 

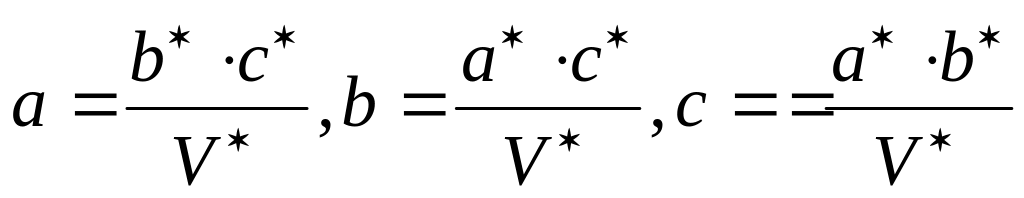
Если между векторами a, b и с прямые, то между векторами тоже 90, направления векторов a и a^, b и b^, с и с^ совпадают.

В моноклинной и триклинной ячейках соотношения более сложные. Вектор a моноклинной ячейки не перпендикулярен плоскости bc, а вектор перпендикулярен ей, тогда , где  - угол межу векторами a и c, ^ = 180 - .

Использование обратной решетки значительно облегчает рассмотрение дифракционной картины.

При выборе другой элементарной ячейки для описания исходной решетки, в случае обратной решетки также получится группа из трех других векторов, но построенная на них решетка будет той же самой, так как векторы узлов обратной решетки определяются только направлением нормалей к семейству плоскостей и величиной межплоскостных расстояний, при этом они не зависят от выбора координатных осей.

Индицирование рентгенограмм порошка. Индицирование рентгенограмм кубических веществ. Закон погасания.

В случае кубической сингонии Q_hkl = A(h²+k²+l²), значения Q_hkl образуют ряд, соответствующий ряду N = h²+k²+l², т.е. Q₁ : Q₂ : Q₃  N₁ : N₂ : N₃. это упрощает индицирование. В данном случае могут отсутствовать некоторые члены ряда, что обусловлено погасаниями, соответствующими той или иной пространственной группе, и носить систематический характер. Часть линий может иметь низкую интенсивность и отсутствовать по этой причине.

Все отражения hkl с нечетной суммой индексов для структуры с ОЦК – решеткой гаснут. Данное утверждение носит название интегрального закона погасания.

Наиболее существенны погасания, вызванные присутствием дополнительных трансляций (в ГЦК – и ОЦК - решетках). В случае примитивной ячейки возможны любые значения hkl и ряд Q_hkl, соответствующий h²+k²+l²; 1,2,3,4,5,6,7,8,9,10 из целых чисел N≤ 30 этот ряд не включает 7, 15, 23, 28.

В ГЦК - ячейке разрешены только те линии с h+k, k+l и h+l = 2n, что соответствует ряду 3,4,8,11,12,16,19,20,24,27.

В случае ОЦК ряд, образуемый Q_hkl, соответствует ряду , так как разрешены только линии с четной суммой индексов. Ряды h²+k²+l² и похожи, но во втором отсутствуют (при N30) N = 14 и 30. Поэтому для того, чтобы однозначно отличить рентгенограммы, соответствующие примитивной и ОЦК – ячейкам, нужно иметь члены ряда до N = 7. Исключая эту неоднозначность, определение индексов этих двух линий может быть проведено если посмотреть, отношение каких чисел соответствует Q₂ : Q₁.