Вариант № 1

Задание № 1. По виду уравнений прямых указать особенности в расположении каждой прямой относительно осей координат и построить отдельно эти прямые в декартовой прямоугольной системе координат.

1) 2x + 3y – 6 = 0;

2) x + y = 0;

3) y – 3 = 0;

4) 2x = 0.

Задание № 2. По эскизам прямых и заданным отрезкам составить уравнения этих прямых.

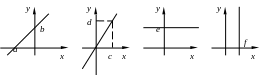
а = 2, b = 4, c = –3, d = –5, e = –1, f = 6.

Задание № 3. Определить и построить кривые:

1) 16x² + 3y² = 48;

2) x² + y² = 4;

3) x² = – 4y.

Задание № 4. По виду уравнений определить типы заданных кривых

1) 4x² + 9y² – 8x – 36y + 4 = 0;

2) x² – 9y² + 2x + 36y – 4 = 0;

3) 2x² – 4x + 2y – 3 = 0.

Задание № 5. Уравнение кривой привести к каноническому виду и построить эту кривую:

9x² + 4y² – 54x – 32y + 109 = 0;

Задание № 6. Построить кривую:

9(y–2)² – x² = 9

Задание № 7. Определить вид кривой и построить ее

x =

Задание № 8. Определить вид кривых и построить их в полярной системе координат:

1) = 2(1 + 2cosφ);

2) = – 5cos3φ;

3) = 3sinφ.

Задание № 9. Определить вид кривых и построить их в декартовой прямоугольной системе координат:

1) , 2) ;

Задание № 10. Даны пять уравнений плоскостей. По их виду указать особенности в расположении каждой плоскости относительно декартовой прямоугольной системы координат и построить отдельно эти плоскости.

1) 5x – 3y – 2z – 7 = 0; 2) 4x – 10y + z = 0;

3) x + z – 1 = 0; 4) 2x + 3y = 0;

5) z – 4 = 0.

Задание № 11. Построить цилиндрические поверхности:

1) ; 2) ; 3) z² = 4x.

Задание № 12. Определить и построить поверхности:

1) x² + 2y² + z² = 4, 2) –x² + 5y² + 5z² = 25;

3) 4x² – y² + 8z² = –16, 4) 5x² + 3y² – z² = 0.

Задание № 13. Определить и построить поверхность:

4x² + y² = 8z.

Задание № 14. Построить тело, ограниченное поверхностями:

y² + z² = 6 – x, x = 0.

Задание № 15. Построить тело, ограниченное поверхностями:

x² + y² + z² = 4, x² + y² = 1, вне цилиндра.

Вариант № 2

Задание № 1. По виду уравнений прямых указать особенности в расположении каждой прямой относительно осей координат и построить отдельно эти прямые в декартовой прямоугольной системе координат.

1) 3x–4y+12=0;

2) 3x–y=0;

3) 2x+1=0;

4) y=0.

Задание № 2. По эскизам прямых и заданным отрезкам составить уравнения этих прямых.

а = 4, b = –2, c = –5, d = 3, e = 4, f = – 8.

Задание № 3. Определить и построить кривые:

1) 9x²+25y²=225;

2) x²–18y²=36;

3) y²=–x.

Задание № 4. По виду уравнений определить типы заданных кривых

1) 36x²+36y²–36x–24y–23=0;

2) 4x²–9y²+6y–1=0;

3) x²–2x+2y–3=0.

Задание № 5. Уравнение кривой привести к каноническому виду и построить эту кривую:

2x² – y² + 4x – 2y – 1 =0.

Задание № 6. Построить кривую:

(y–2)² = 2x – 1.

Задание № 7. Определить вид кривой и построить ее

.

Задание № 8. Определить вид кривых и построить их в полярной системе координат:

1) =–5sin3φ;

2) =3cosφ;

3) =2(1–cosφ).

Задание № 9. Определить вид кривых и построить их в декартовой прямоугольной системе координат:

1) ; 2) .

Задание № 10. Даны пять уравнений плоскостей. По их виду указать особенности в расположении каждой плоскости относительно декартовой прямоугольной системы координат и построить отдельно эти плоскости.

1) 2x+6y+5z–13=0; 2) x+2y–3z=0;

3) y+2z–8=0; 4) 4x+5y=0;

5) 4x+9=0.

Задание № 11. Построить цилиндрические поверхности:

1) 2) ; 3) x² = 2z.

Задание № 12. Определить и построить поверхности:

1) 3x² + y² + 2z² = 6; 2) 4x² + 8y² – z² = –8;

3) 9x² – 2y² + 3z² = 18; 4) –x² + 2y² + 3z² = 0.

Задание № 13. Определить и построить поверхность:

y² + 4z² = 16x.

Задание № 14. Построить тело, ограниченное поверхностями:

x² + z² = (y – 2)², y = 4, y = 0.

Задание № 15. Построить тело, ограниченное поверхностями:

x² + y² = 6z, x² + y² = 24, z = 0.