Задача побудови найкоротших радіальних маршрутів між вузлами мережі перевезень пошти

У поштовому зв’язку радіальні маршрути використовуються, в основному, як магістральні та регіональні маршрути, а в разі нестачі часу для проходження кільцевих маршрутів – також як окружні маршрути.

Задача формулюється так: заданий зв’язний зважений граф, вершини якого відповідають вузлам мережі перевезень пошти, ребра – шляхам, що з’єднують ці вузли, а ваги ребер – протяжністю відповідних шляхів. Знайти найкоротші шляхи, що з’єднують задану початкову вершину з рештою вершин графа.

Розв’язання задачі засновано на формуванні рельєфу графа у виді ваг вершин графа, значення яких дорівнюють значенням протяжністю найкоротших шляхів між ними і початковою вершиною графа.

Початковій вершині В_і надається вага Р_і = 0, решті вершин – нескінченні ваги Р_j = .

На кожному кроці формування рельєфу графа знаходиться раніше неперевірена вершина мінімальної ваги, відносно якої формуються ваги тих неперевірених вершин, що безпосередньо з’єднані з перевірною вершиною. Вага неперевіреної вершини замінюється вагою перевірної вершини, збільшеної на вагу ребра, що з’єднує зазначені вершини, якщо перша перевищує другу.

Разом з формуванням рельєфу формується інформація про значення ваги кожної вершини і про номер вершини, від якої ця вага отримана.

Найкоротші шляхи формуються як послідовності записів зазначеної інформації, прочитані в порядку, зворотному до їхнього формування.

Алгоритм формування рельєфу графа наведений на рис. 1.

Початок

1. Присвоєння початковій вершині

ваги Р_i = 0, присвоєння решті

вершин ваг Р_j = 999

2. Вибір серед неперевірених вершин

графа вершини В_k мінімальної ваги

3. Обчислення ваги = P_k + P_(k,j)

чергової неперевіреної вершини

B_j графа, безпосередньо пов’язаної

з перевірною вершиною B_k

Ні

4.  Р_j

Так

5. Р_j = , запис B_k

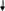
6. Всі

вершини B_j, безпосередньо Ні

пов’язані з вершиною B_k,

перевірені

Так

7. Присвоєння перевірній вершині

B_k позначки “перевірена” (*)

Ні 8. Перевірено

n - 1 вершин графа

Так

Кінець

Рисунок 1 – Алгоритм формування рельєфу графа

Алгоритм містить 8 блоків.

У блоці 1 створюється початковий рельєф графа. Початковій вершині В_і присвоюється мінімальна вага Р_і = 0, решті вершин графа B_j (j = 1, 2, … n, j  i) – нескінченні ваги Р_j = , які подаються як надмірні ваги Р_j = 999.

У блоці 2 серед неперевірених вершин вибирається вершина В_k мінімальної ваги Р_k.

У блоці 3 обчислюється вага = Р_k + Р_(k,j) чергової неперевіреної вершини B_j відносно перевірної вершини B_k, що безпосередньо пов’язана з вершиною B_j графа.

У блоці 4 обчислена вага порівнюється з вагою Р_j вершини B_j. При  Р_j виконується перехід до блока 5, при  Р_j – до блока 6.

У блоці 5 вага Р_j замінюється вагою , тобто значення ваги вершини B_j знижується, і запам’ятовується вершина B_k, від якої одержано значення ваги Р_j .

У блоці 6 перевіряється, чи всі вершини В_j графа, безпосередньо пов’язані з перевірною вершиною B_k, перевірені. Якщо так – здійснюється перехід до блока 7, якщо ні – повернення до блока 3.

У блоці 7 перевірній вершині B_k присвоюється позначка “перевірена” (*) і вона виключається з подальшого розгляду.

У блоці 8 перевіряється кількість вершин графа, що вже перевірені. Якщо таких вершин менше n - 1 – здійснюється повернення до блока 2, і процес формування рельєфу графа повторюється, якщо їх n - 1 – рельєф графа сформований і робота алгоритму закінчується.

Алгоритм формування найкоротших шляхів за сформованим рельєфом графа наведено на рис. 2.

Алгоритм містить 5 блоків.

У блоці 1 фіксується поточна перевірна вершина B_l = B_j (j = 1, 2, … n,

j  i).

У блоці 2 виконується зчитування рядка l таблиці рельєфу графа.

У блоці 3 фіксується значення номера попередньої вершини B_k графа та ваги Р_l .

У блоці 4 значення l замінюється значенням k, тобто поточна вершина B_l замінюється поточною вершиною B_k графа.

У блоці 5 порівнюються значення l і i. При l  i виконується повернення до блока 2 і формування шляху між вершинами B_i та B_j графа продовжується. При l = i шлях між вершинами B_i та B_j графа сформований і робота алгоритму закінчується.

Наведені алгоритми формування рельєфу графа (рис. 1) і формування найкоротших шляхів за сформованим рельєфом графа (рис. 2) можуть бути використані також для формування шляхів, найкоротших за числом проміжних вершин. У задачах поштового зв’язку такі шляхи використовуються для перевезень важкої (посилкової) пошти з метою скорочення витрат, пов’язаних з її перевантаженням у транзитних вузлах.

Початок

1. l = j (j = 1, 2 …, n, j  i)

2. Зчитування рядка l таблиці

рельєфу графа

3. Запис номера попередньої

вершини B_k графа і ваги P_l

4. l = k

Ні 5. l = i

Так

Кінець

Рисунок 2 – Алгоритм формування найкоротших шляхів

Приклад побудови найкоротших радіальних маршрутів між обласними вузлами мережі перевезень пошти України

Таблиця 1 –Формування рельєфу графа

Таблиця 2 –Формування рельєфу графа

Крок 1
Bі	*	Рi = 0	Вк=12
1. Луцьк		∞
2. Львів		∞
3. Ужгород		∞
4. Рівне		∞
5. Тернопіль		∞
6. Ів.-Франківськ		∞
7. Житомир		139	12
8. Хмельницький		∞
9. Чернівці		∞
10. Чернігів		138	12
11. Вінниця		∞
12. Київ	*	0
13. Миколаїв		∞
14. Одеса		463	12
15.Черкаси		214	12
16. Полтава		327	12
17. Суми		320	12
18. Харків		∞
19. Кіровоград		298	12
20. Херсон		∞
21. Сімферополь		∞
22. Запоріжжя		∞
23. Дніпропетровськ		∞
24. Донецьк		∞
25. Луганськ		∞

Крок 0
Ві	*	Pi	Вк
1. Луцьк		∞
2. Львів		∞
3. Ужгород		∞
4. Рівне		∞
5. Тернопіль		∞
6. Ів.-Франківськ		∞
7. Житомир		∞
8. Хмельницький		∞
9. Чернівці		∞
10. Чернігів		∞
11. Вінниця		∞
12. Київ		0
13. Миколаїв		∞
14. Одеса		∞
15.Черкаси		∞
16. Полтава		∞
17. Суми		∞
18. Харків		∞
19. Кіровоград		∞
20. Херсон		∞
21. Сімферополь		∞
22. Запоріжжя		∞
23. Дніпропетровськ		∞
24. Донецьк		∞
25. Луганськ		∞

Таблиця 27 – Перелік найкоротших шляхів

12-7-4-1
12-7-4-2
12-7-4-2-3
12-7-4
12-7-8-5
12-7-8-5-6
12-7
12-7-8
12-7-8
12-7-8-9
12-10
12-7-11
12-19-13
12-14
12-15
12-16
12-17
12-16-18
12-19
12-19-13-20
12-19-13-20-21
12-19-23-22
12-19-23
12-16-18-24
12-16-18-25