§ 3. Интегрирование по частям

Из формулы дифференциала произведения следует формула интегрирования по частям . Интегрирование по частям применяется, как правило, тогда, когда под интегралом имеется произведение алгебраической и неалгебраической функций, например, или . При этом за u принимается функция, которая при дифференцировании упрощается, а за – та часть подынтегрального выражения, содержащая dx, интеграл от которой известен или может быть вычислен. Если под интегралом стоит произведение логарифмической или обратной тригонометрической функции на алгебраическую, то за u обычно принимают неалгебраическую функцию, если - произведение тригонометрической или показательной функции на алгебраическую, то за u принимается алгебраическая функция.

П р и м е р 1. Вычислить .

► Пусть x = u , тогда sin x dx = . Следовательно, du = dx , а , таким образом,

Проделанные вычисления показывают, что постоянную можно не учитывать, поэтому в дальнейшем при вычислениях опускается. ◄

П р и м е р 2. Вычислить .

► Пусть Следовательно, du = dx, а Поэтому, ◄

П р и м е р 3. Вычислить .

 Пусть тогда x dx = и, следовательно, ,

. Таким образом,

◄

П р и м е р 4 . Вычислить

► Полагаем arctg x = u, тогда dx = , поэтому

;

Значит, ◄

В задачах 297-332 вычислить интегралы

297. . 298. . 299. 300.

301. 302. 303.

304. 305. 306. 307.

308. 309. 310. 311.

312. 313. 314. 315.

316. 317. 318. 319.

320. 321. 322. 323.

324. 325. 326.

327. 328. 329.

330. 331. 332.

§ 4 Экономические задачи, сводящиеся к вычислению определенных интегралов

4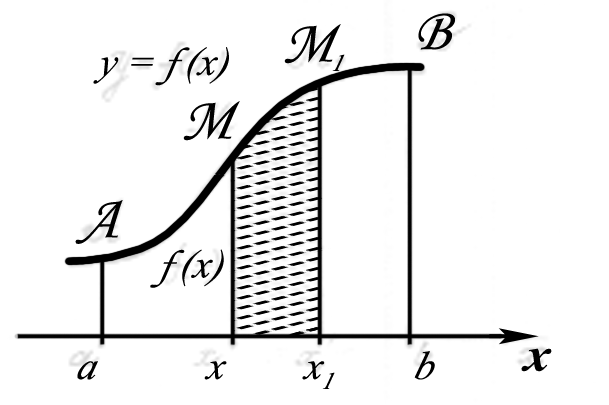 .1. Экономический смысл определенного интеграла. Определенный интеграл представляет собой предельное значение интегральной суммы составляющих искомой величины. Поэтому экономический смысл определенного интеграла так же, как геометрический и физический его смысл, определяется смыслом интегральных составляющих, то есть смыслом подынтегрального выражения f(x)dx. Геометрически f(x) – высота криволинейной трапеции, а – ее основание, поэтому произведение f(x) dx представляет собой площадь малой криволинейной трапеции xMM₁x_1. (рис. 10) Определенный интеграл представляет сумму площадей, малых криволенейных трапеций, составляющих площадь фигуры аАВb, то есть . С помощью определенного интеграла, таким образом, можно вычислить площадь любой фигуры геометрически неправильной формы.

Если х – время , f(x) – скорость движения в момент времени x, а dx – предельно малый временной интервал, столь малый, что скорость движения в течение этого времени можно считать постоянной, равной то – малый элемент пути, пройденного со скоростью f(x) за время dx, (дифференциал пути ). Сумма таких малых элементов пути дает весь путь, пройденный за время – весь путь s , пройденный за конечный временной интервал . Действительно, S = = .

Если х – количество продукции, f(x) – предельные издержки (издержки, связанные с производством следующей за х, (х+1) – ой, единицы продукции), а dx – предельно малый объем производства, столь малый, что издержки по производству каждой единицы продукции этого объема, то есть f(x), можно считать постоянными, то произведение f(x)dx представляет собой издержки по производству этого малого объема продукции (дифференциал издержек ). А определенный интеграл дает издержки производства заданного конечного объема продукции, когда объем производства меняется в пределах . Итак, издержки .

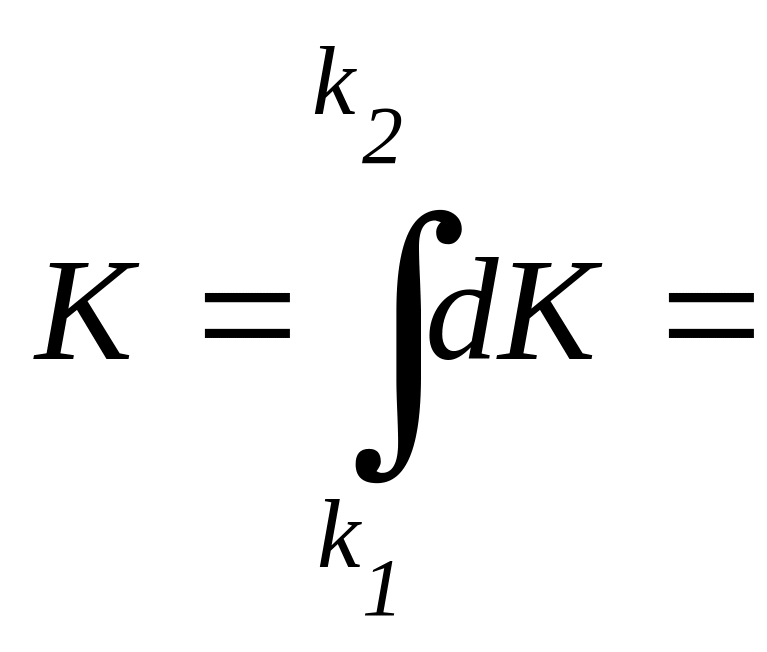Если х – время, f (x) – производительность ^ труда, а dx – предельно малый временной интервал, то производительность труда, являющуюся функцией времени, можно считать постоянной на этом временном интервале. Тогда произведение даст объем продукции, произведенной за время, равное dx, то есть предельно малый объем продукции; дифференциал объема . А определенный интеграл даст сумму таких малых объемов, равную объему продукции, произведенной за конечный временной интервал .

П р и м е р 1. Определить объем продукции, произведенной рабочим за второй час рабочего дня, если производительность труда характеризуется функцией .

► Искомый объем определяется по формуле .

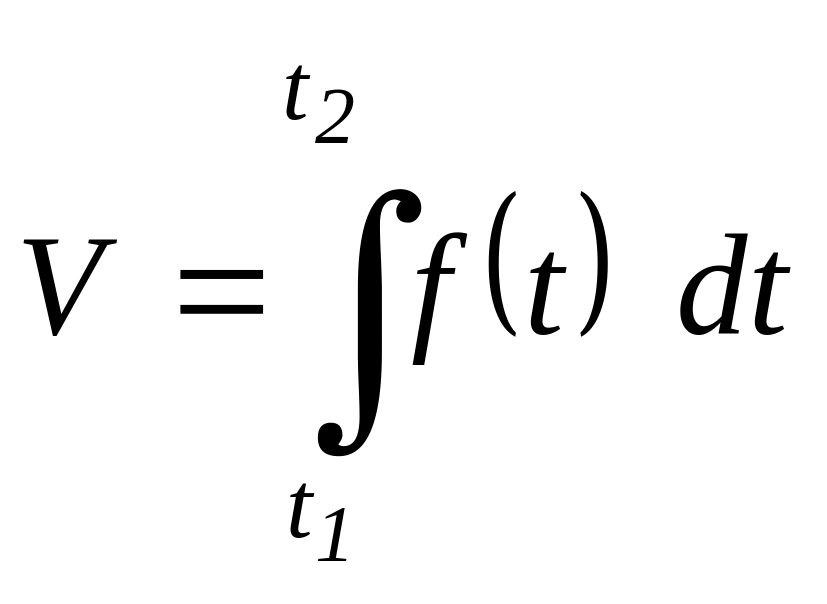Действительно, – функция производительности труда. Она дает объем продукции, производимой за единицу времени. Производительность труда не постоянна, она является функцией времени. Если dt – очень малый промежуток времени, то можно считать, что производительность труда за это время не изменится, оставаясь постоянной и равной .

Тогда объем продукции , произведенной за время dt, можно найти как произведение f(t) dt. А продукцию, выпущенную за второй час рабочего дня найдем как сумму таких микрообъемов то есть определенный интеграл , где . Итак,

◄

З амечание. При вычислении знак модуля под логарифмом опущен, так как время t не может быть отрицательным и, следовательно, 3t + 4 > 0.

П р и м е р 2. Для оценки степени неравенства в распределении доходов среди населения исследуют кривую Лоренца, показывающую зависимость процента доходов от процента имеющего их населения (кривая ОВА, рис. 11). При равномерном распределении доходов кривая Лоренца вырождается в прямую – биссектрису ОА.

Cтепень неравенства в распределении доходов среди населения характеризуется коэффициентом Джини, представляющим собой отношение площади сегмента ОАВ между биссектрисой ОА и кривой Лоренца к площади прямоугольного треугольника ОАС.

Вычислить коэффициент Джини, если распределение доходов описывается уравнением , где х – доля населения, у – доля доходов.

► Согласно определению, коэффициент Джини равен

, так как .

^) ,

Чтобы вычислить этот интеграл, будем считать, что тогда а . Найдем, в каких пределах меняется новая переменная интегрирования t, когда . При х = 0, при = Итак, имеем

, таким образом

Достаточно высокое значение R говорит о существенно неравномерном распределении доходов среди населения. ◄

333. По данным исследований распределения доходов в одной из стран кривая Лоренца описывается уравнением , где – доля населения, – доля доходов населения. Вычислить коэффициент Джини.

334. Найти среднее значение издержек производства, если предельные издержки R(x) равняются , а объем продукции х меняется от 0 до 3 ед. Указать объем продукции, при котором предельные издержки равны средним издержкам.

335. Определить объем продукции, произведенной рабочим за пятый час рабочего дня, если производительность труда изменяется со временем в соответствии с функцией .

⁾ Дробь является неправильной, если показатель степени переменной в числителе больше или равен показателю степени переменной в знаменателе.

^ Производительность труда есть объем продукции, производимой в единицу времени

⁾ Здесь подынтегральное выражение представляет собой доход dx – ой доли населения, а определенный интеграл, геометрически дающий представляет собой суммарный доход населения страны.