3.2. Асинхронные трехфазные двигатели

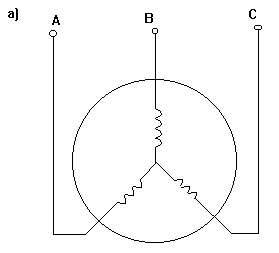
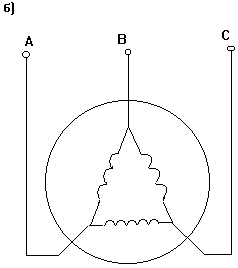
В асинхронном трехфазном двигателе вращающееся магнитное поле создается тремя обмотками статора, на которые подается трехфазное напряжение сети.

Схема трехфазного двигателя и временная диаграмма питающего напряжения показаны на .

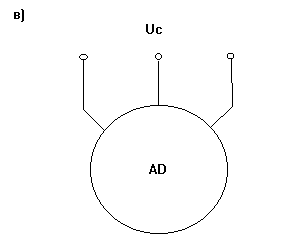
Рис. 3-6а,б,в. Схемы включения асинхронного двигателя.

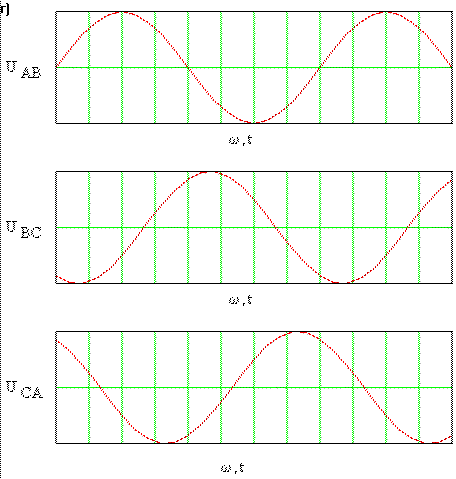
Рис. 3-6г. Временная диаграмма питающих напряжений асинхронного двигателя.

Для двигателей основной является механическая характеристика ω=f(M), то есть зависимость частоты вращения от момента, которая для асинхронного двигателя может быть получена на основании выражения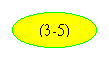или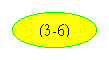с учетом связи между скольжениемSи частотой вращения ω. Вид механической характеристики показан на.

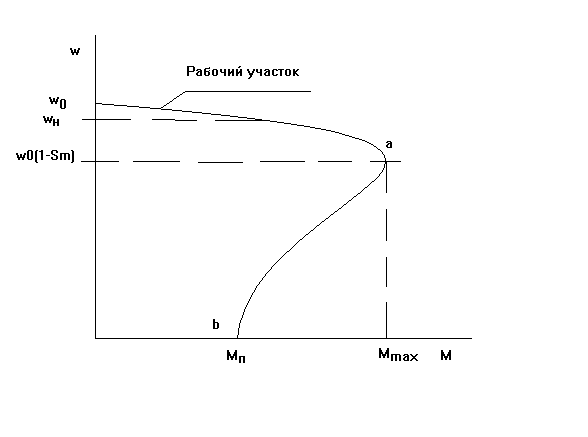
Рис. 3-7а. Механическая характеристика асинхронного трехфазного двигателя.

Ее можно разбить на два участка - рабочий (0-а) при 0<S<S_Mи участок пуска (a-b) приS_M<S<1. Обычно в асинхронных трехфазных двигателях с короткозамкнутым роторомS_M=0.05..0.15, т.е. характеристики достаточно жесткие и рабочая частота вращения ω_нблизка к синхронной ω₀. Для таких двигателей на рабочем участке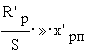т.е. преобладает активная составляющая сопротивления ротора. Тогда, пренебрегая в формуле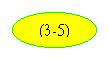сопротивлениямиx´_рп иr₁по сравнению с, получим упрощенное выражение для рабочего участка механической характеристики

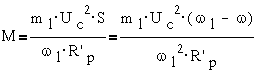
откуда

,

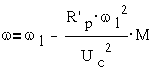
где ω - частота вращения ротора, ω₁- частота вращения поля,U_c- напряжение питания сети,R´_p- приведенное сопротивление ротора. Как видно из выраженияи, изменение напряжения питания мало влияет на частоту вращения ротора на рабочем участке и диапазон управления напряжением весьма ограничен.

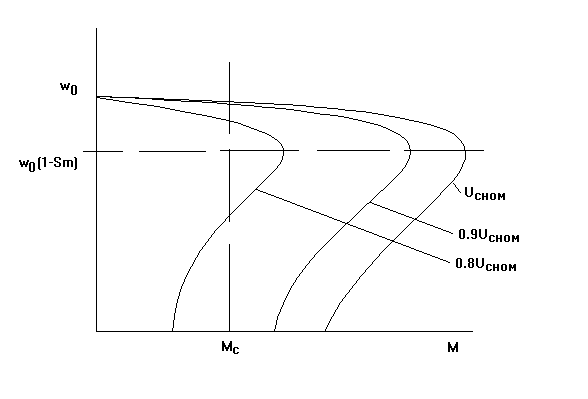
Рис. 3-7б. Механическая характеристика асинхронного трехфазного двигателя.

Несколько больший диапазон может быть обеспечен двигателем повышенного скольжения (S_M≥1). Однако в этом случае механические характеристики имеют большую крутизну () и устойчивая работа двигателя может быть достигнута лишь при использовании замкнутой системы, обеспечивающей стабилизацию скорости. При изменении статического момента система регулирования поддерживает заданный уровень скорости и происходит переход с одной механической характеристики на другую, в итоге работа протекает на характеристиках, показанных наштриховыми линиями.

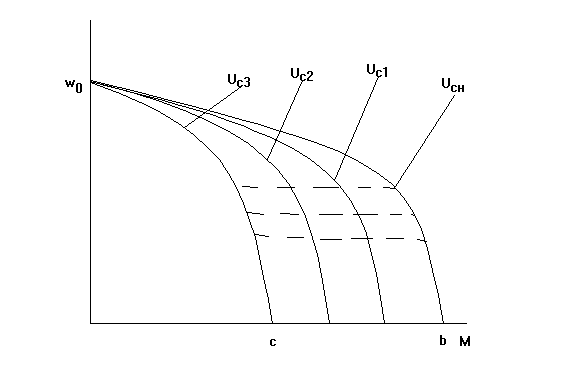
Рис. 3-7в. Механическая характеристика асинхронного трехфазного двигателя.

Плавное регулирование скорости в широких пределах с сохранением достаточной жесткости характеристик возможно только при частотном управлении. Как видно из формулы , изменяя частоту вращения поля ω₁, можно изменять частоту вращения ротора ω за счет первого слагаемого формулы, при этом желательно, чтобы второе слагаемое не менялось, т.е. жесткость характеристики при этом не изменялась. Для этого одновременно с частотой, изменяют напряжение питанияU_cтак, чтобы их отношение оставалось постоянным.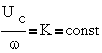

Тогда рабочий участок механической характеристики при частотном управлении можно приближенно представить формулой:

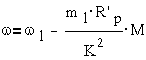
Такое управление называется пропорциональным частотным управлением.

Вид механических характеристик при пропорциональном управлении показан на .

Рис. 3-8а. Частотное управление асинхронным двигателем.

Функциональная схема частотного управления представлена на . Она состоит из управляемого выпрямителя УВ, преобразующего сетевое напряжение переменного тока частотой 50 Гц в напряжение питания постоянного токаU_п, величина которого может регулироваться от устройства управления УУ, и автономного инвертора АИ, преобразующего напряжениеU_пв трехфазное напряжение изменяемой частотыf₁. Управляющее устройство, изменяя частотуf_1вв зависимости от задания ω_з, изменяет также и напряжениеU_птак, чтобы их отношение оставалось постоянным. Система управления может иметь обратную связь по скорости вращения через тахогенератор ТГ.

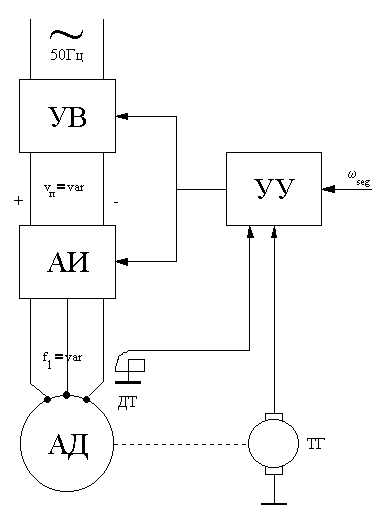
Рис. 3-8б. Функциональная схема частотного управления.

Более совершенным, чем пропорциональное управление, является частотно-токовое управление, при котором контролируется, кроме частоты вращения, ток якоря от датчика тока (ДТ), как показано на , что позволяет оставлять постоянным поток при изменении частотыf₁и нагрузки.

Как динамическая система асинхронный трехфазный двигатель описывается нелинейным дифференциальным уравнением первого порядка:

,

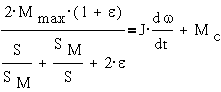где J- момент инерции ротора.

Учитывая, что ω=ω₀·(1-S) и, и принимая ε=0, получим:

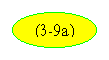
Учитывая, что ,получим:

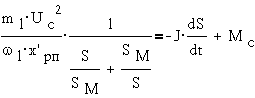
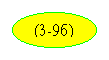
Этому уравнению соответствует структурная схема, представленная на .

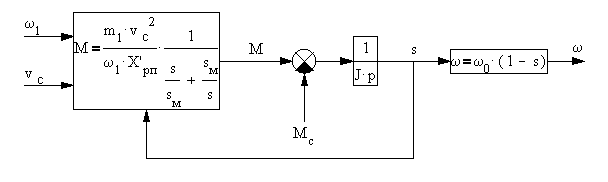
Рис. 3-9а. Структурная схема асинхронного трехфазного двигателя.

Интегрируя уравнение () в пределах отS₁доS, получим

,

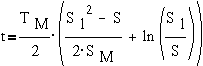
где 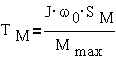- электромеханическая постоянная времени.

Выражение (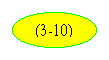) позволяет построит кривые переходного процессаS=f(t) и соответственно ω=f(t), вычисляя ряд значенийtпри неизменномS₁и изменяющемсяS. Кривые разгона двигателя при различныхS_Mприведены на. Как видно, длительность переходного процесса существенно зависит отS_Mи при некотором значенииS_{M_опт}минимальна. Двигатели повышенного скольжения являются более быстродействующими, так какS_{M_опт}≈0.4..0.5.

При пропорциональном частотном управлении для малых приращений двигатель можно описать линейными уравнениями (см. 3-1)

Этим уравнениям соответствует структурная схема, представленная на .

Рис. 3-9в. Структурная схема асинхронного трехфазного двигателя.

На основании анализа этой схемы можно получить передаточную функцию двигателя при частотном управлении

,

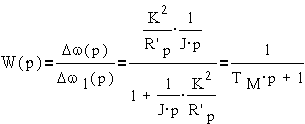где K- электромеханическая постоянная времени.