60. Оператор Гамильтона.

Многие операции векторного анализа могут быть записаны в сокращенной и удобной форме с помощью символического оператора Гамильтона «набла»:

( формальное умножение на функцию будем понимать как дифференцирование

1). Если – скалярная дифференцируемая функция, то

.

2). Если где - дифференцируемые функции, то

3). Если то

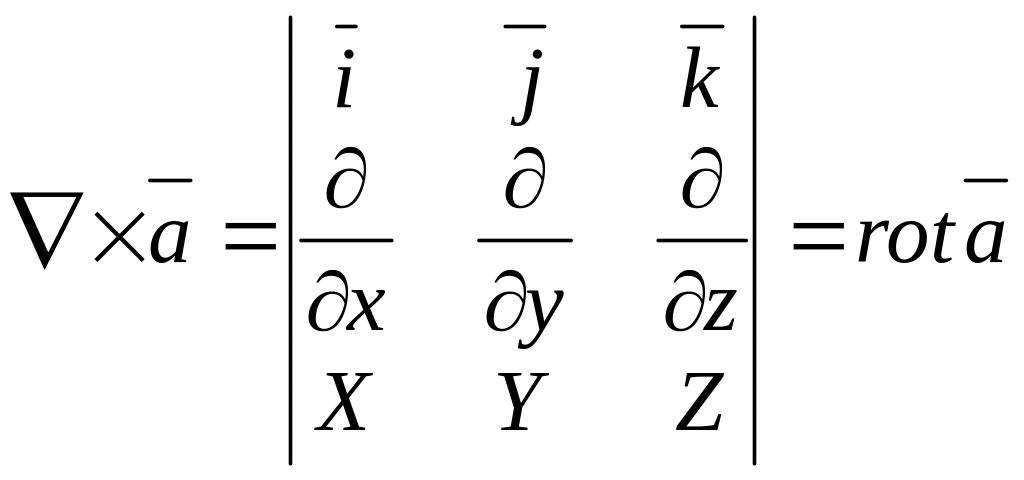
В результате двукратного применения к полям оператора получаем дифференцируемые операции второго порядка. Если задано скалярное поле , то оператор порождает в нем векторное поле . В векторном поле оператор , примененный повторно к , дает:

а) скалярное поле (2.10)

б) векторное поле (2.11)

Если задано векторное поле то оператор порождает в нем:

1. скалярное поле , в этом скалярном поле порождает векторное поле

; (2.12)

2. векторное поле 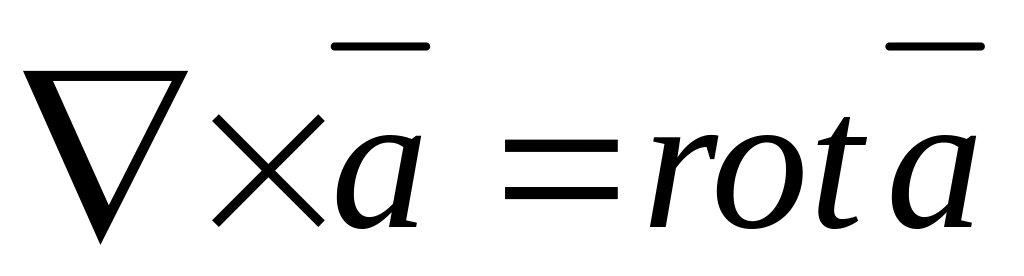, в этом векторном поле порождает:

а) скалярное поле (2.13)

б) векторное поле (2.14)

Формулы (2.10)-(2.14) определяют дифференциальные операции второго порядка;

Если имеет непрерывные частные производные до второго порядка включительно, то (2.11)

Действительно,

,

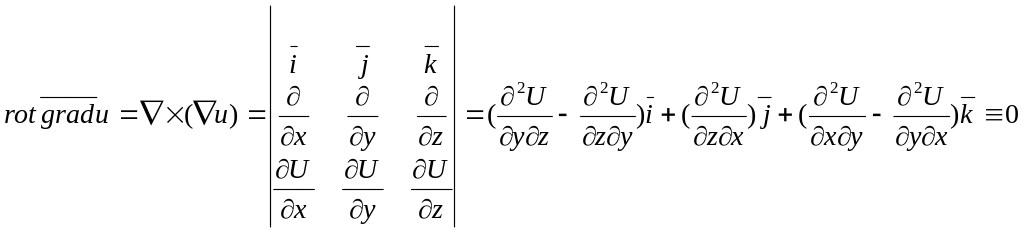т.к. смешанные производные равны.

Аналогично, если причем имеют непрерывные частные производные второго порядка, то (2.13):

Рассмотрим теперь (2.10) , предполагая, что имеет частные производные второго порядка по

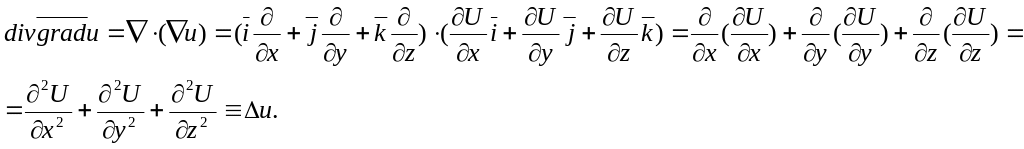
Здесь символ называется оператором Лапласа.

.