60.Вычисление поверхностных интегралов

Разберем вычисление интеграла Пусть поверхность σ задана уравнением

Преобразуем интегральную сумму

,

где это проекция на плоскость , взятая со знаком .

Левая часть последнего равенства представляет собой интегральную сумму для двойного интеграла. Если перейти к пределу при стягивании в точку, то получим

где – проекция на плоскость , а знак выбирается в зависимости от угла нормального вектора к поверхности с осью . Аналогичные формулы можно получить для интегралов:

следовательно искомый интеграл равен:

Пример 9.

Вычислить поверхностный интеграл где – внешняя сторона параболоида , ограниченная плоскость .

Н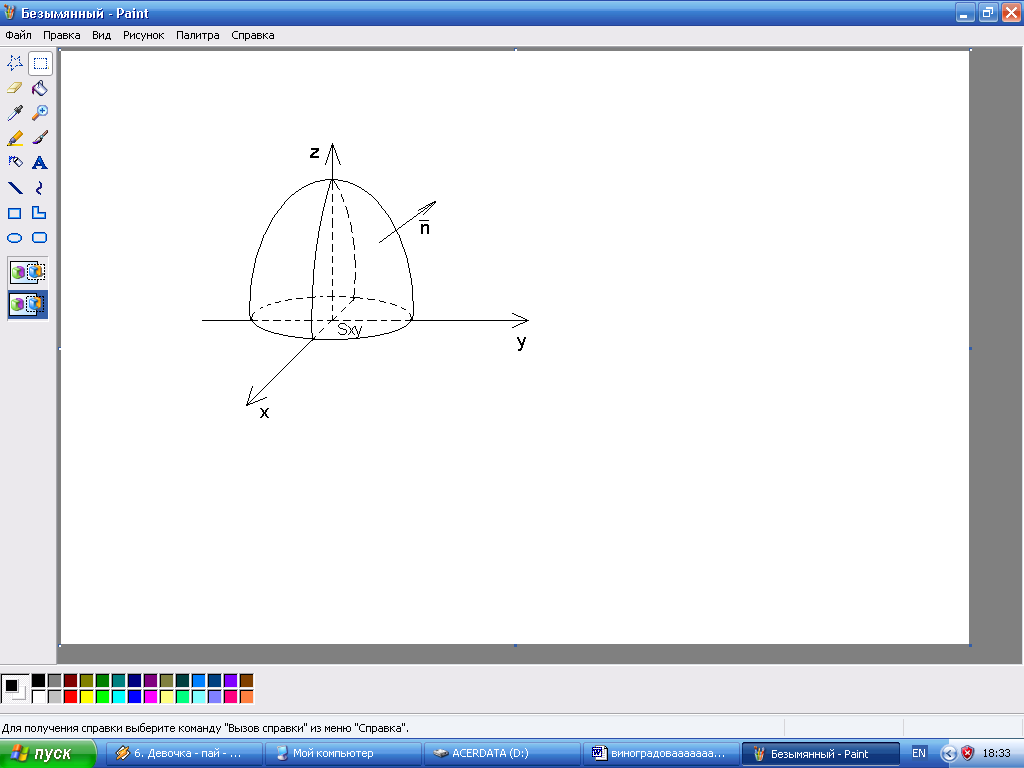 ормаль к поверхности образует острый угол с осью (ось, перпендикулярная плоскости проекции), поэтому при переходе к двойному интегралу знак не меняется. Выразим из уравнения поверхности

Найдем интеграл

Вычисление поверхностного интеграла свелось к вычислению двойного интеграла, который будем брать, переходя к полярным координатам:

Итак,

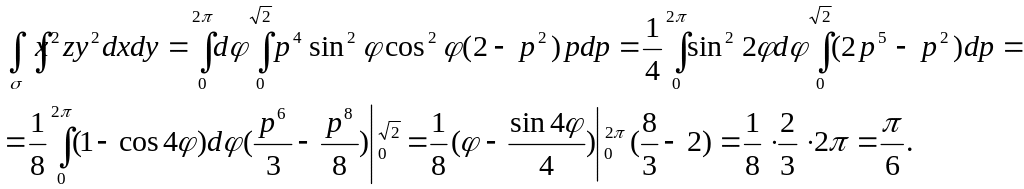
Пример 10.

Вычислить поверхностный интеграл где – внешняя сторона поверхности цилиндра вырезанная цилиндром

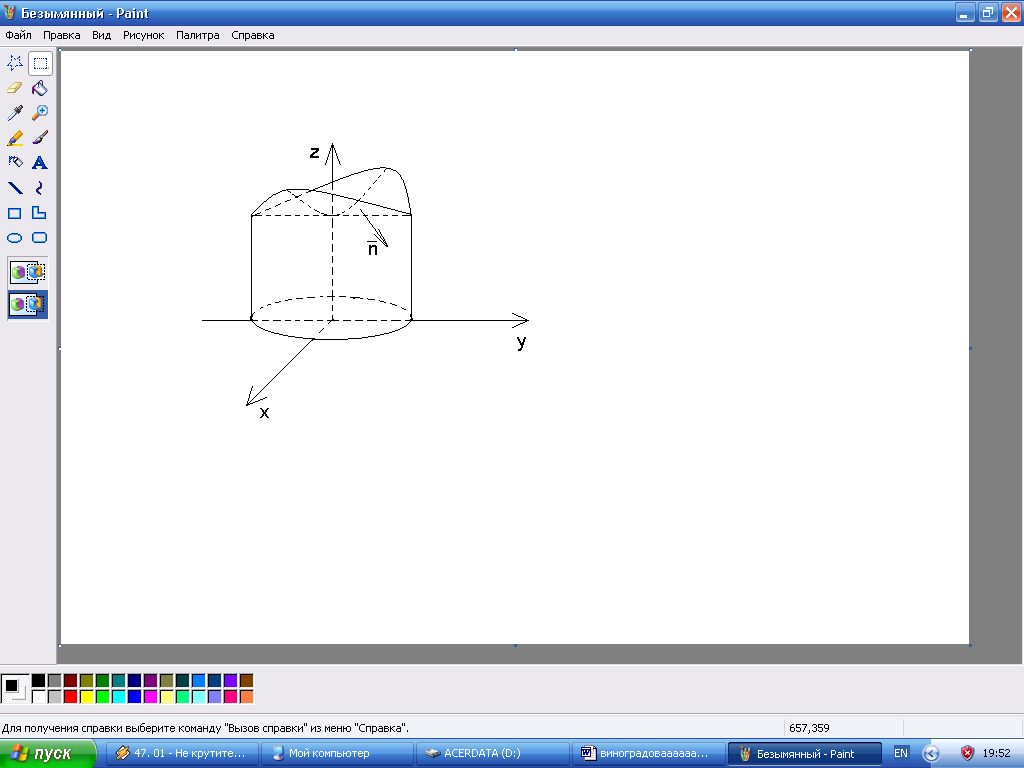
Нормаль к внешней поверхности цилиндра образует тупой угол с осью которая перпендикулярна плоскости проекций Поэтому при переходе от поверхностного интеграла к двойному, знак меняется на противоположный.

Здесь из уравнении поверхности цилиндра . Полученный двойной интеграл разобьем на два интеграла, один из которых будем брать в полярных координатах.

Имеем

.

Положим

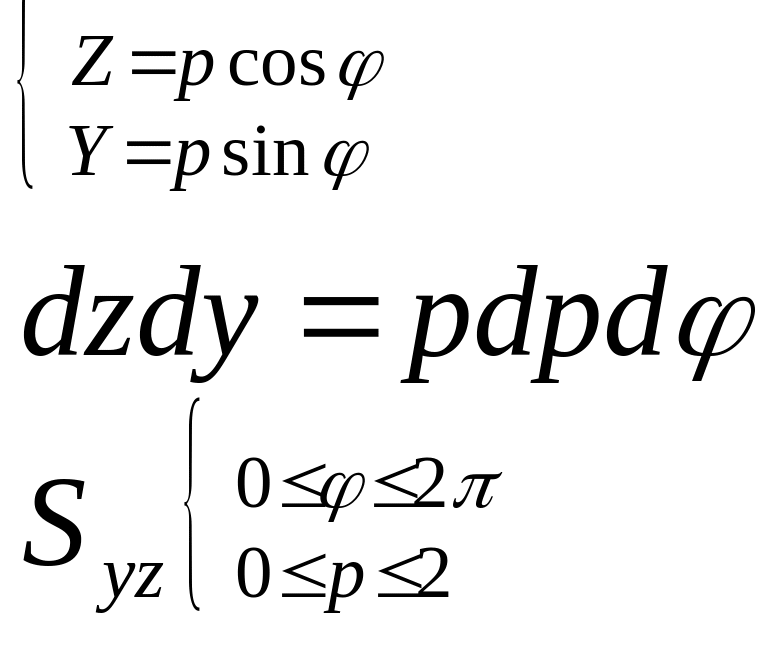
Итак, поверхностный интеграл

Ответ:

Пример 11.

Вычислить поверхностный интеграл

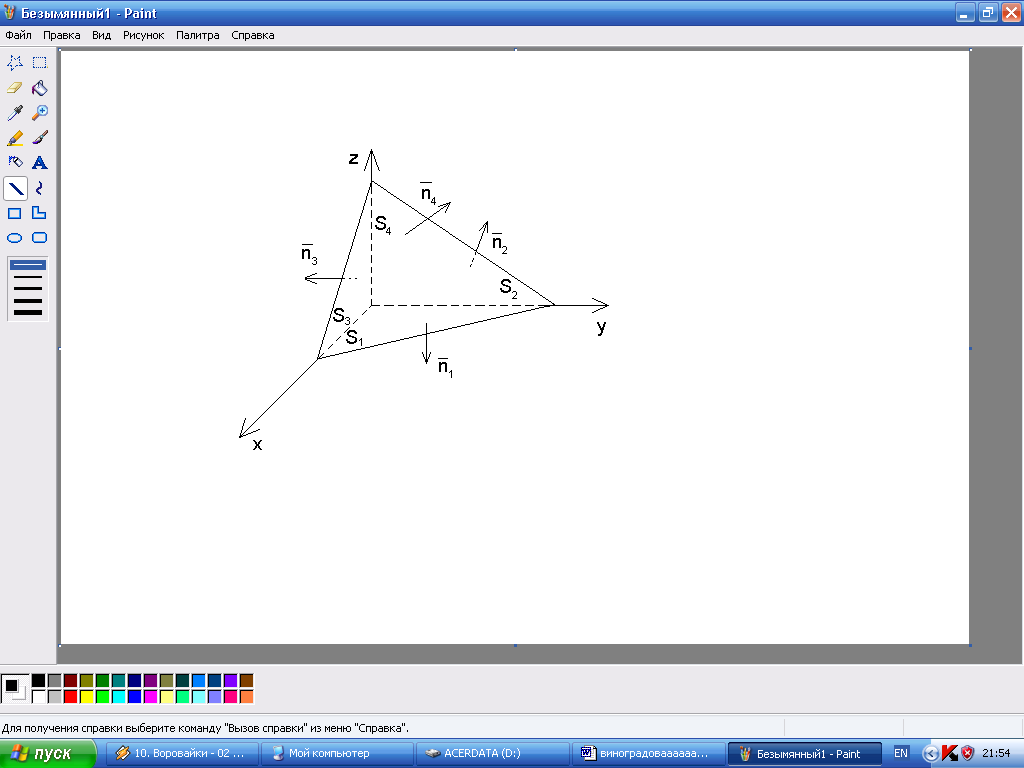
где – внешняя сторона пирамиды

Уравнения поверхностей

Представим данный интеграл в виде суммы трех интегралов, каждый из которых затем вычислим по четырем поверхностям

где соответствующие обозначения интегралов. Интеграл следует брать по поверхностям так как остальные поверхности будут давать нулевую площадь проекции.

Знак «минус» в первом случае потому, что нормаль к внешней стороне пирамиды образует тупой угол с осью Во втором интеграле знак , так как нормаль образует острый угол с положительным направлением оси Уравнение подставив вместо его выражение из уравнения поверхности, получаем, что первый интеграл равен нулю. Итак, имеем

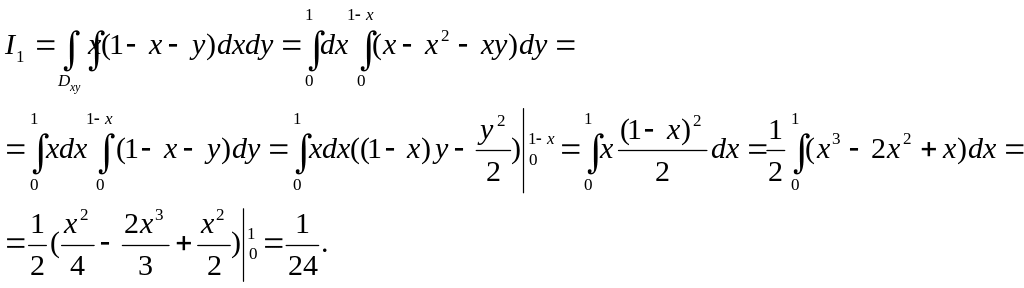
Рассуждая аналогично, вычислим второй интеграл:

Уравнение

Уравнение откуда

Итак,

т. к. это тот же интеграл, что мы вычисляли выше, но с другими обозначениями переменных.

Наконец, вычислим интеграл

Окончательно,

Ответ:

Пример 12.

Вычислить поверхностный интеграл

г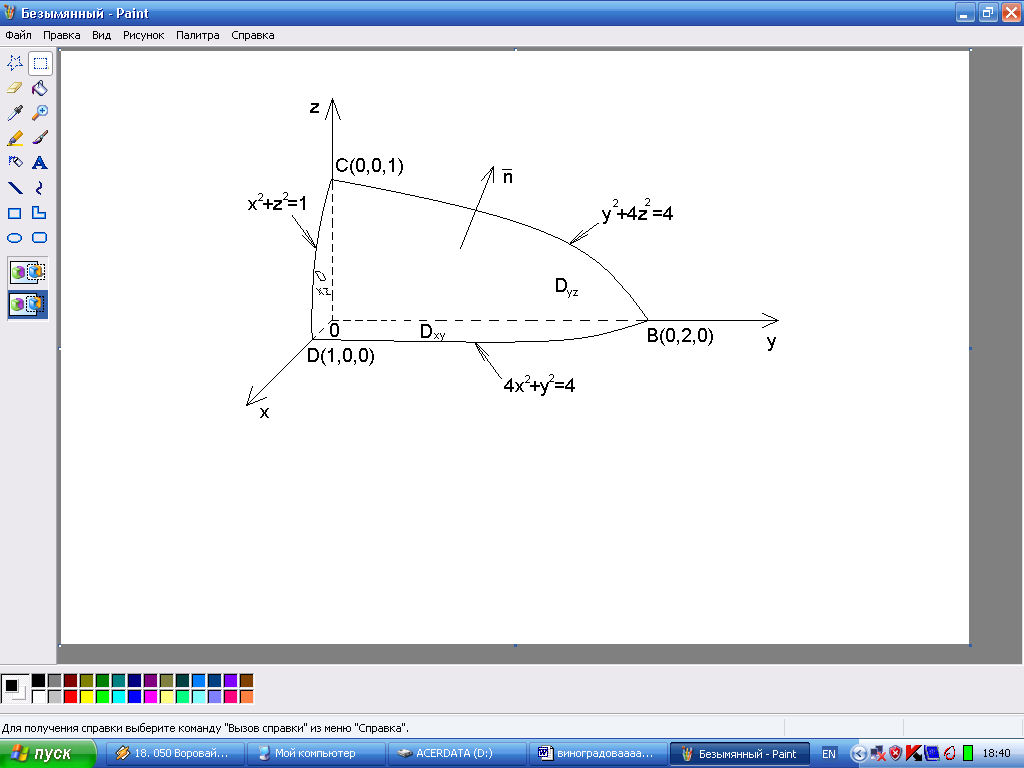 де – внешняя сторона части эллипсоида , расположенной в первом октанте.

Разобьем данный поверхностный интеграл на три слагаемых интеграла.

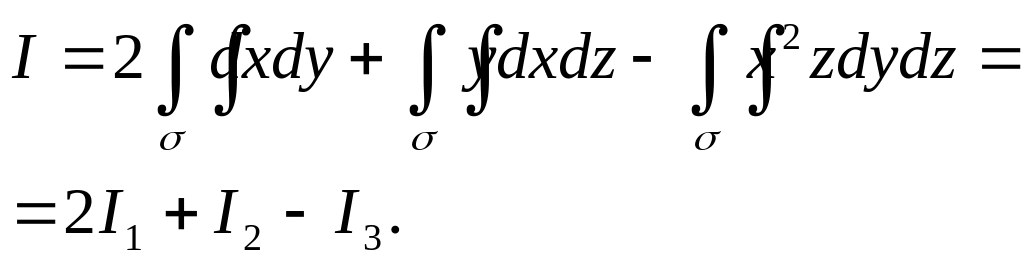
Нормаль образует острый угол со всеми положительными направлениями осей координат, поэтому знак не меняется

где - проекция на плоскость – четверть эллипса (площадь эллипса с полуосями вычисляется по формуле ).

где - часть круга Для вычисления этого интеграла перейдем к полярным координатам

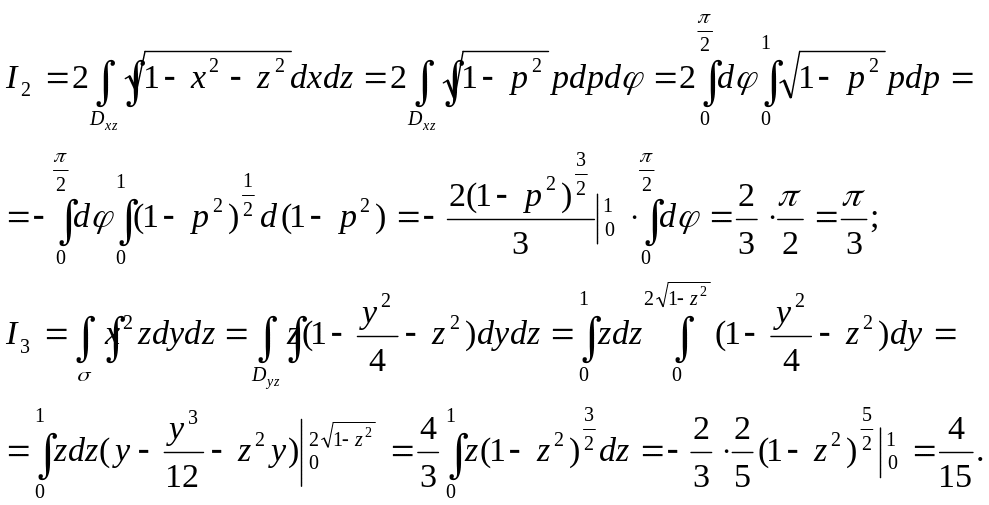
Следовательно,