- •Часть 1
- •Криволинейный интеграл второго рода
- •Связь криволинейных интегралов первого и второго родов. Специфическое свойство интеграла второго рода
- •Вычисление криволинейного интеграла 2-го рода
- •40. Формула грина
- •50. Поверхностный интеграл 2-го рода
- •60.Вычисление поверхностных интегралов
- •70. Формулы остроградского и стокса
- •70. Условия независимости криволинейного интеграла от пути интегрирования
- •90. Восстановление функции по ее полному дифференциалу
- •Часть 2
- •10. Поток векторного поля
- •20.Поток вектора через замкнутую поверхность. Дивергенция векторного поля.
- •30. Линейный интеграл в векторном поле. Циркуляция векторного поля.
- •40. Ротор (вихрь) векторного поля. Теорема Стокса.
- •50. Некоторые типы векторных полей.
- •60. Оператор Гамильтона.
30. Линейный интеграл в векторном поле. Циркуляция векторного поля.
Линейным интегралом
от векторного
![]() вдоль кривой
вдоль кривой
![]() называется криволинейный интеграл
называется криволинейный интеграл
![]() (2.5)
(2.5)
В том случае, когда
вектор
![]() является вектором силы (поле
является вектором силы (поле
![]() является силовым полем), линейный
интеграл (2.5) дает величину рабрты этого
поля вдоль линии
(см. 10
ч. 1).
является силовым полем), линейный
интеграл (2.5) дает величину рабрты этого
поля вдоль линии
(см. 10
ч. 1).
Пример 6.
В каждой точке
плоскости на материальную точку действует
сила
![]() .
Вычислить работу силы
.
Вычислить работу силы
![]() при перемещении точки из начала координат
в точку
при перемещении точки из начала координат
в точку
![]()
1) по прямой
![]()
2) по параболе
![]()
3) по ломаной
![]()
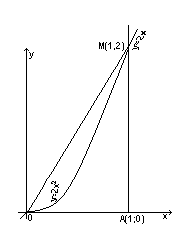
Решение: Решение:
Работа переменной силы вдоль
криволинейного участка пути
определяется по формуле:
![]()
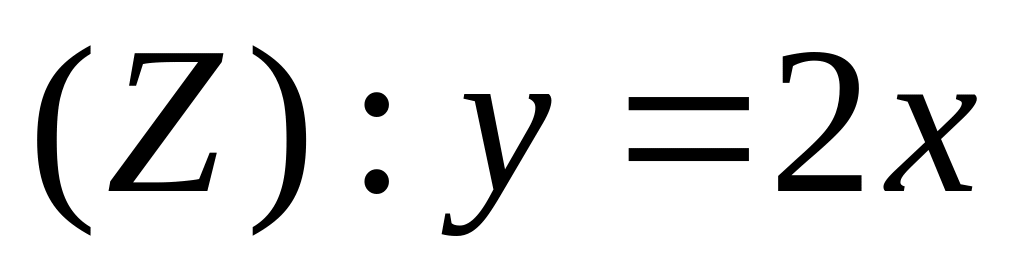 из
из
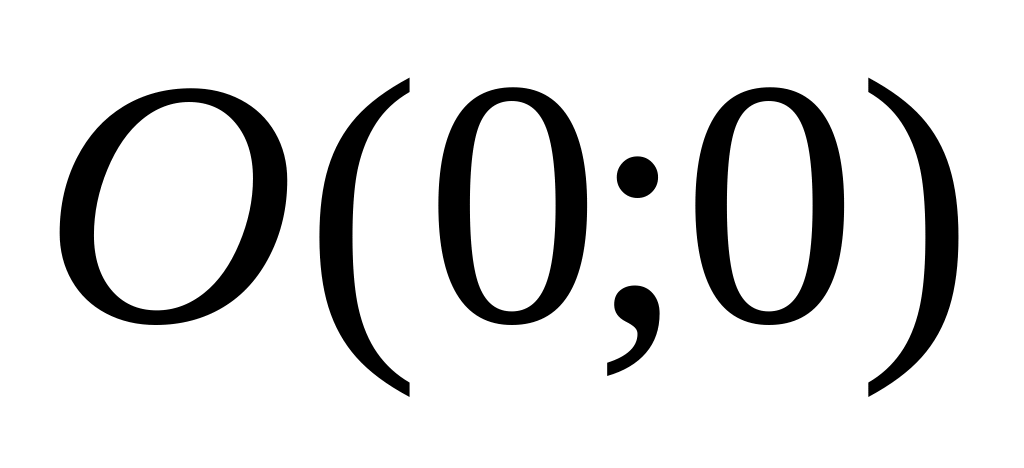 в
в
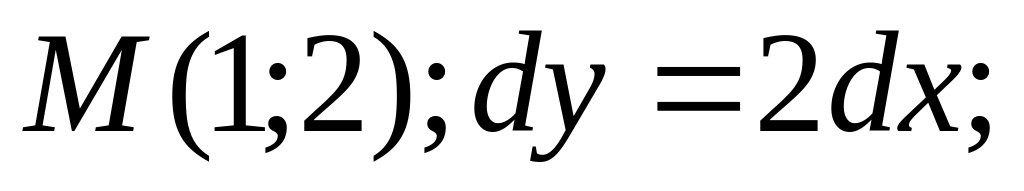
![]()
![]()
: два звена ломаной
 .
Уравнения звеньев ломаной
.
Уравнения звеньев ломаной
![]()
![]()
Следовательно,
работа вдоль
![]() .
Если контур
замкнутый, то линейный интеграл
.
Если контур
замкнутый, то линейный интеграл
![]() называется циркуляцией
векторного поля
вдоль контура
.
называется циркуляцией
векторного поля
вдоль контура
.
40. Ротор (вихрь) векторного поля. Теорема Стокса.
Пусть имеем поле вектора
![]()
Будем предполагать, что функция непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам.
Ротором
вектора
называется вектор, обозначаемый символом
![]() и определяемый равенством
и определяемый равенством
![]() (2.6)
(2.6)
Для заполнения этой формулы удобно ввести символическую форму
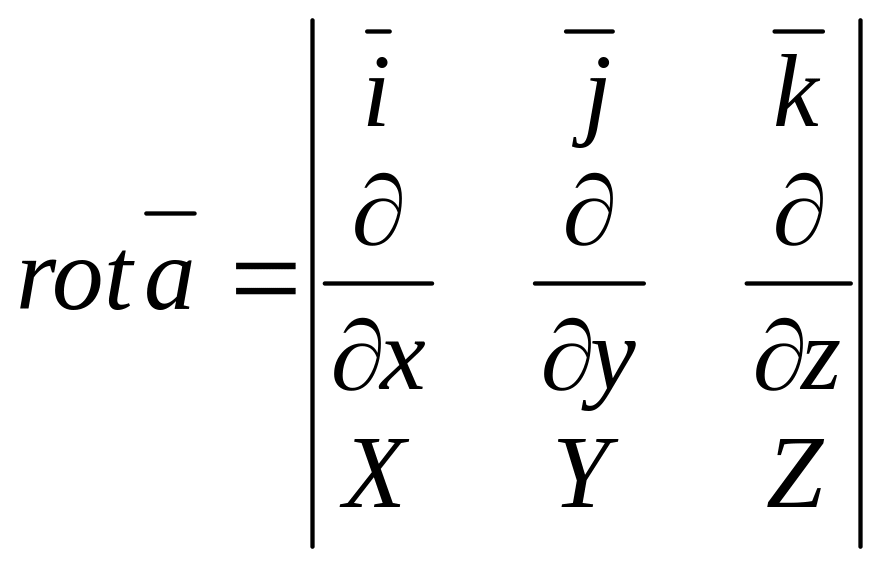 (2.61)
(2.61)
Этот определитель
раскрывается по элементам первой строки,
операцию умножения элементов второй
строки на элементы третьей, понимают
как операцию дифференцирования (
например,
![]()
Пример 7.
Пусть задано поле
вектора
![]()
Определить
![]() в произвольной точке.
в произвольной точке.
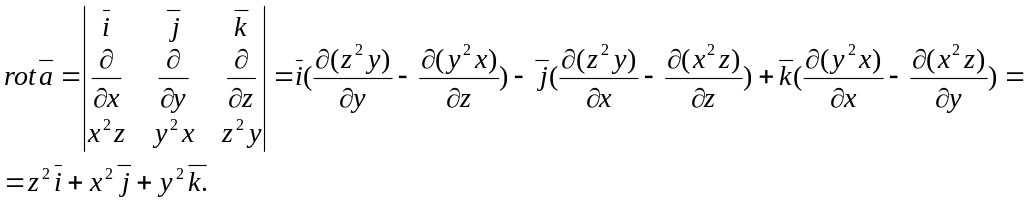
Пример 8.
Рассмотрим
произвольное движение твердого тела.
Из кинематики известно, если фиксировать
в нем точку
![]() ,
то для любого момента времени поле
скоростей точек тела определяется
следующей формулой
,
то для любого момента времени поле
скоростей точек тела определяется
следующей формулой
![]()
где
![]() - скорость точки
,
- скорость точки
,
![]() - мгновенная угловая
скорость,
- мгновенная угловая
скорость,
- радиус-вектор, соединяющий точку с любой точкой тела .
 Возьмем
некоторую систему координат,
Возьмем
некоторую систему координат,
начало которой совпадает с точкой .
Найдем
![]() .
.
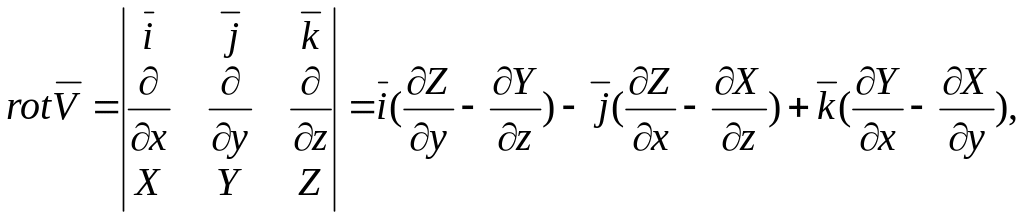
(*).
Где
– проекции вектора
![]() на оси координат. Исходя из формулы
на оси координат. Исходя из формулы
![]() найдем
найдем
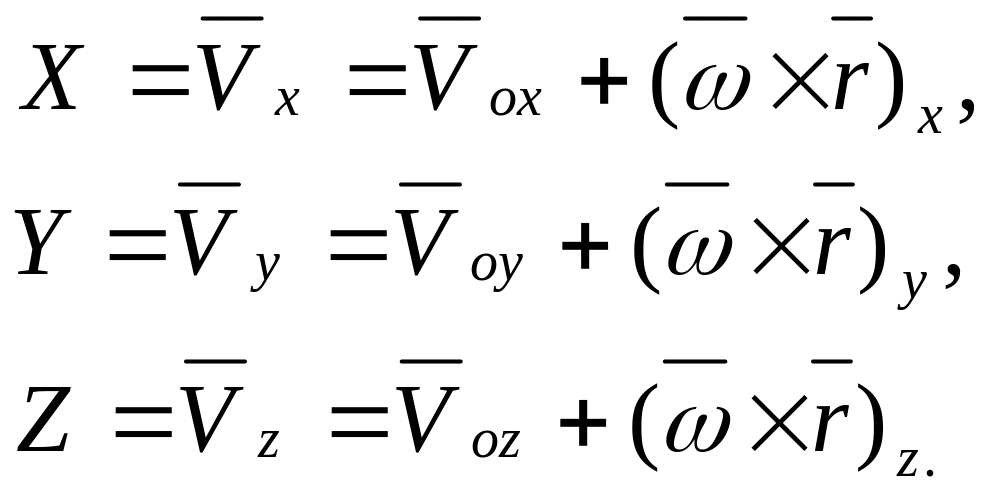
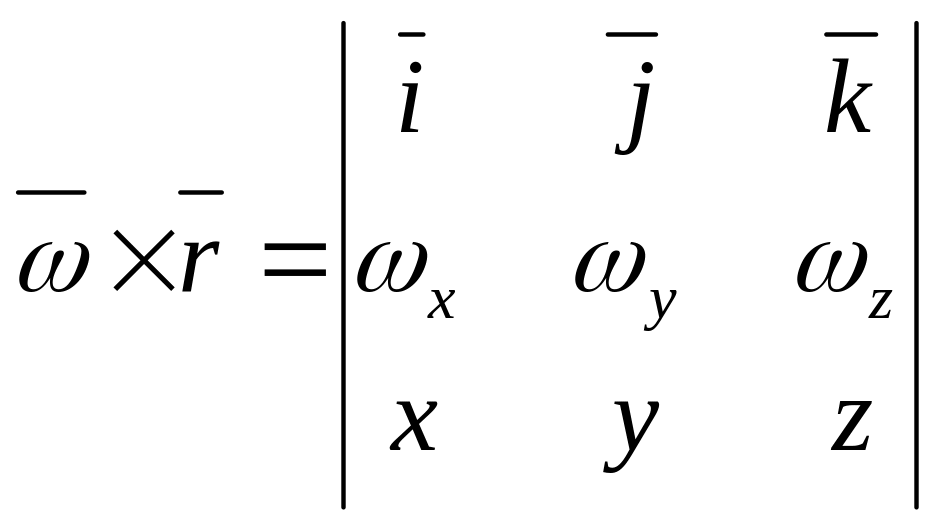
где
![]() – проекция вектора
(или координаты точки M),
– проекция вектора
(или координаты точки M),
![]() - координаты вектора
,
откуда
- координаты вектора
,
откуда
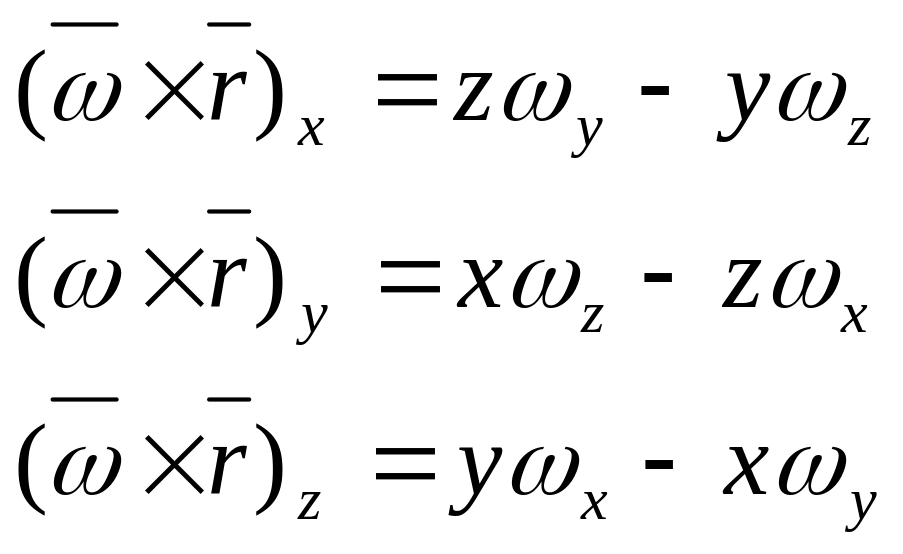
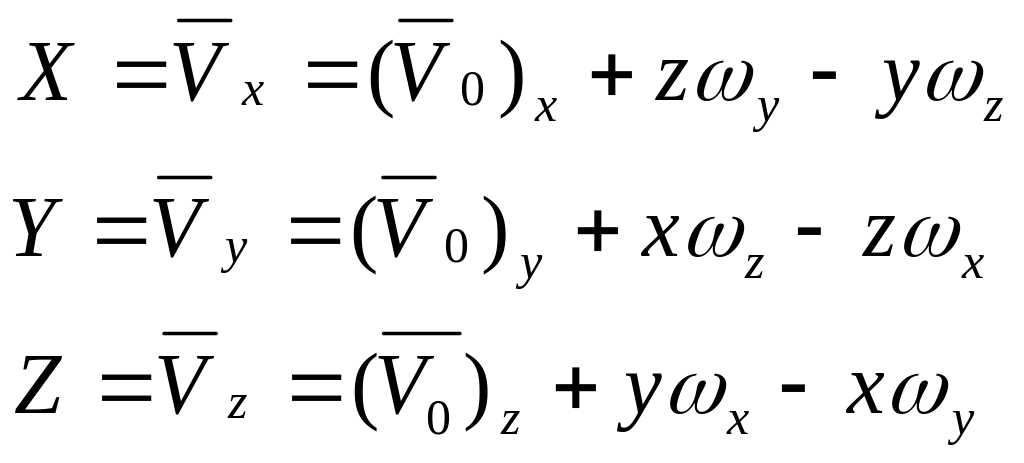
Дифференцируя эти равенства, получим
![]()
![]()
![]()
![]()
![]()
![]()
Подставим эти значения частных производных в формулу (*) :
![]()
Таким образом, rot
совпадает с
![]() (удвоенный вектор угловой скорости).
(удвоенный вектор угловой скорости).
Физический смысл вихря.
Пусть
![]() - произвольное направление, проходящее
через точку
и
- произвольная малая плоская площадка,
проходящая через точку
нормально и
(
- произвольное направление, проходящее
через точку
и
- произвольная малая плоская площадка,
проходящая через точку
нормально и
(![]() - граница
).
Применим формулу Стокса
- граница
).
Применим формулу Стокса
![]()
Воспользуемся теоремой о среднем :
![]()
где
![]() – некоторая точка площадки
.
– некоторая точка площадки
.
Если
![]() то
то
![]()
Переходя к пределу, получим значение проекции в точке на произвольное направление
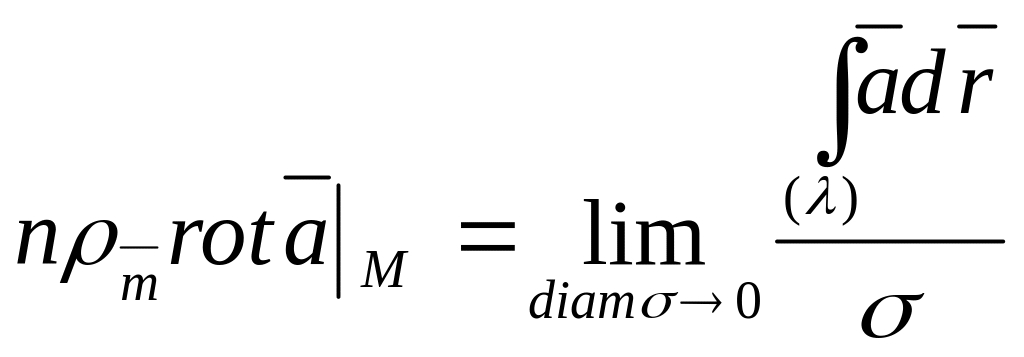
Формула Стокса в векторной форме имеет вид
![]() (2.7)
(2.7)
т.е. циркуляция вектора вдоль контура некоторой поверхности равна потоку ротора через эту поверхность.
Пример 9.
Вычислить циркуляцию
вектора
![]() вдоль окружности
вдоль окружности
![]()
используя формулу
Стокса. Взять в качестве поверхности
полусферу
![]() .
Интегрирование по окружности в плоскости
.
Интегрирование по окружности в плоскости
![]() ведется против часовой стрелки.
ведется против часовой стрелки.
Решение.
По формуле Стокса
![]()
Определим
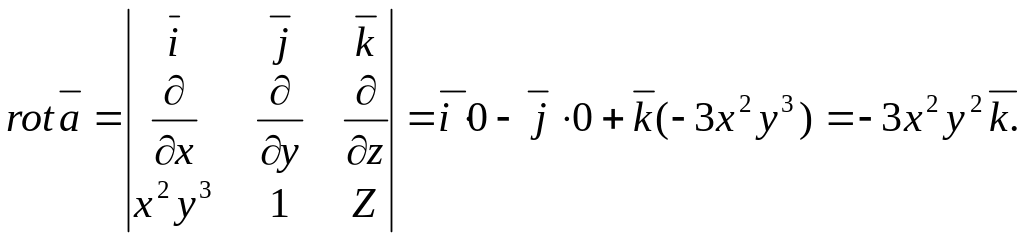
Определим координаты
нормали
![]() тогда
тогда
![]()
Учитывая положительный
обход окружности, делаем вывод, что
нормаль к поверхности полусферы образует
острый угол с осью
![]() .
Перейдем от поверхности интеграла к
двойному по области, ограниченной
заданной окружностью
.
Перейдем от поверхности интеграла к
двойному по области, ограниченной
заданной окружностью