50. Некоторые типы векторных полей.

1) Если во всех точках некоторой области дивергенция векторного поля равна нулю ( , то говорят, что поле соленоидально в этой области. Соленоидальное поле не может иметь ни источников, ни стоков.

Из формулы (2.2) следует, что соленоидальном поле поток вектора через любую замкнутую поверхность лежащую в этом поле, равен нулю

Пример 10.

Показать, что поле напряженности , точечного заряда соленоидально, т.е. Найдем дивергенцию вектора

но

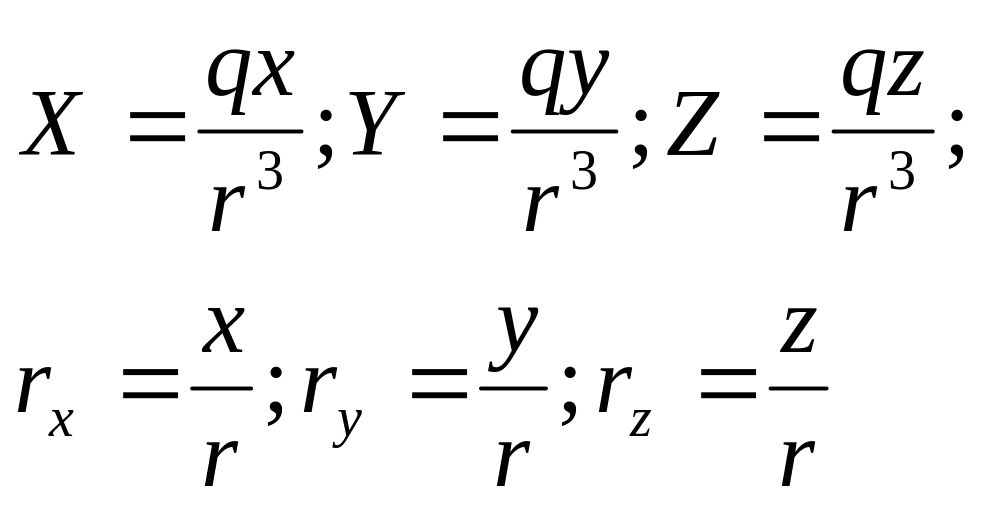
(это определяется из выражения ). Следовательно,

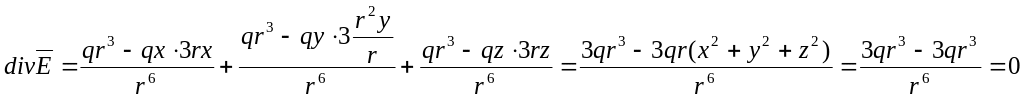
всюду, где

Пример 11.

Показать, что после магнитной напряженности соленоидально всюду, за исключением начала координат. Найдем но

Следовательно,, ч. 1)

2) Если в каждой точке области то поле вектора в области называется безвихревым.

3) Векторное поле называется потенциальным, если линейный интеграл этого поля не зависит от формы пути или, что то же самое (см. 8⁰ , ч. 1), если циркуляция векторного поля вдоль каждого замкнутого пути равна нулю.

Итак, для потенциальности векторного поля

необходимо и достаточно, чтобы криволинейный интеграл

не зависел от формы пути, а это выполняется тогда и только тогда, когда является полным дифференциалом некоторой функции , т.е. справедливы равенства (см. 8⁰, 9⁰ ч.1) или

Следствие 1. Для того, чтобы векторное поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым.

Следствие 2. Для того, чтобы векторное поле было потенциальным, необходимо и достаточно, чтобы оно было полем градиентов некоторого поля.

Поле потенциально тогда и только тогда, когда , т.е. или, учитывая, что получаем

Функция называется потенциалом (потенциальной функцией) векторного поля

Потенциал векторного поля определяется равенством (9⁰, ч. 1)

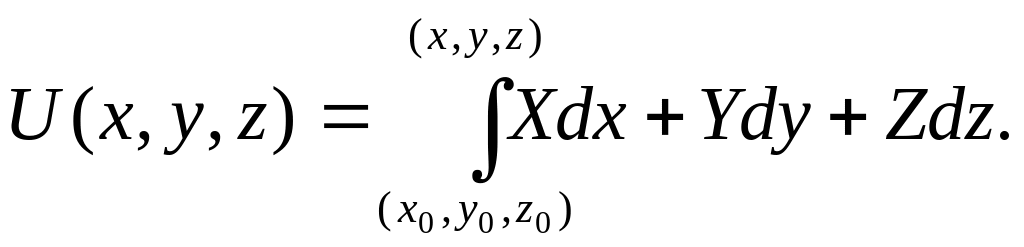(2.8)

где – фиксированная точка поля, – произвольная текущая точка.

Линейный интеграл в потенциальном поле равен разности значений потенциала поля в конечной и начальной точках пути интегрирования

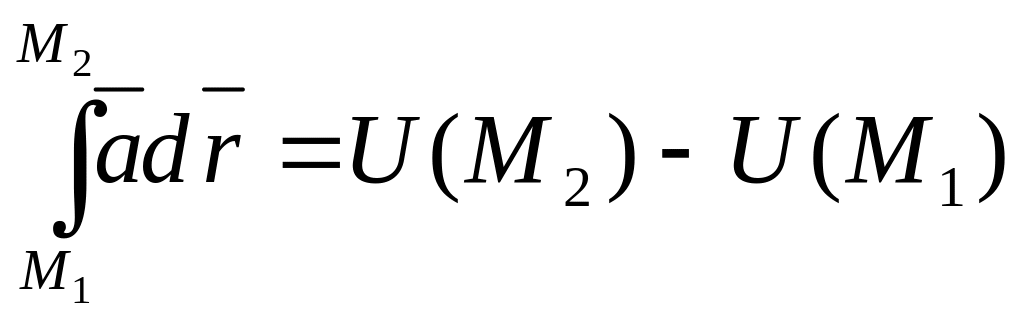(2.9)

Пример 12.

Рассмотрим поле напряженности точки заряда . Найдем вихрь этого поля.

Пусть заряд находится в точке .

Построим некоторую прямоугольную

систему координат, начало которой

совпадает с точкой . - радиус-век-

тор произвольной точки поля. Пусть

координаты его будут Тогда

и координаты век-

тора будут

Итак,

(1)

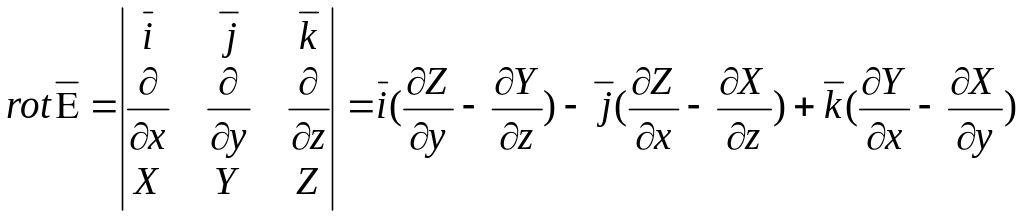(2)

Из равенства (1) найдем

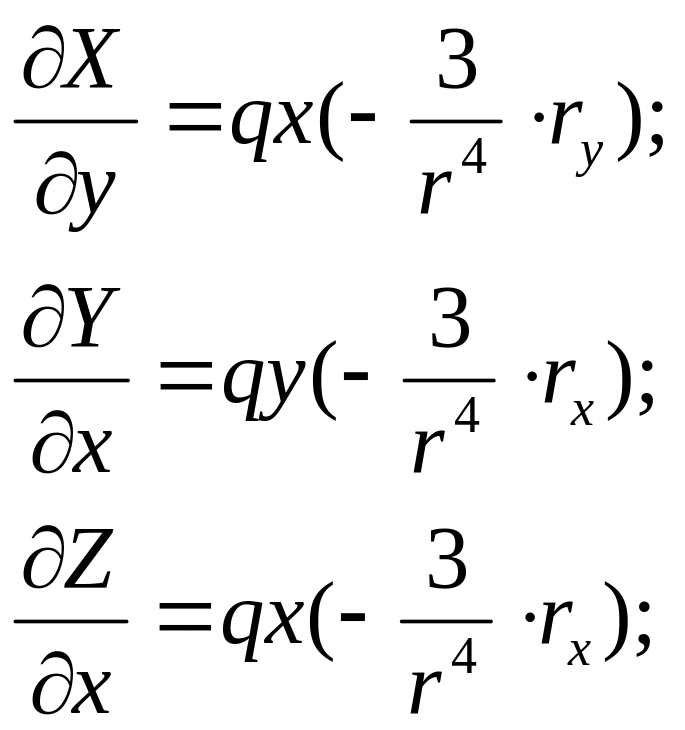
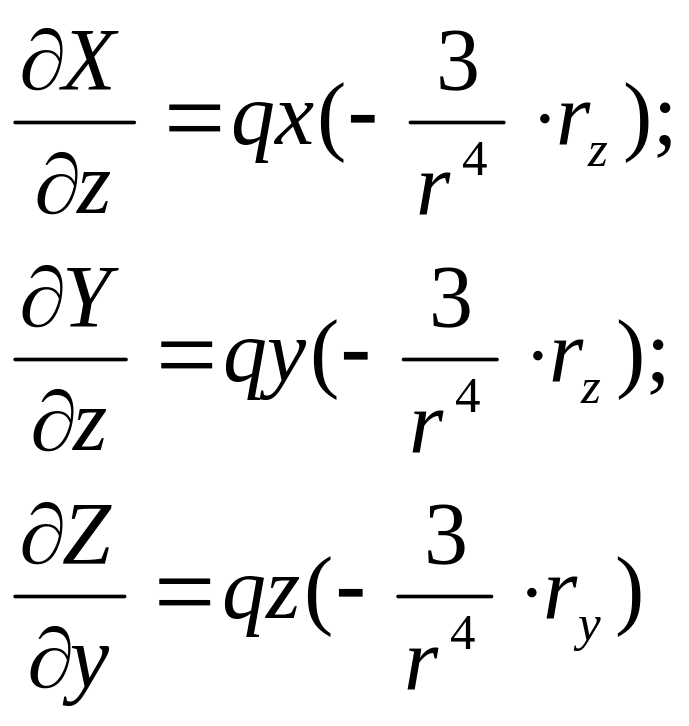
И так как , получим

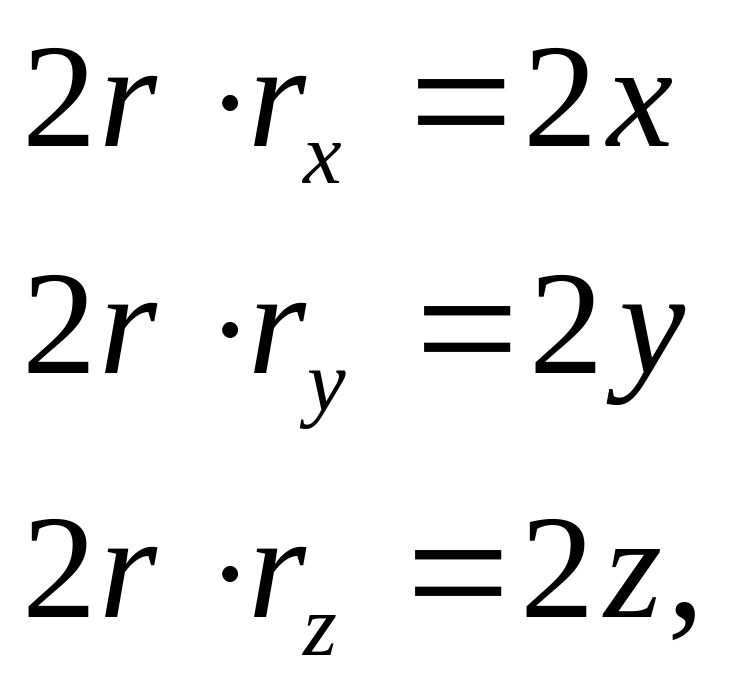
откуда

Подставляя значения частных производных в равенство (2) находим

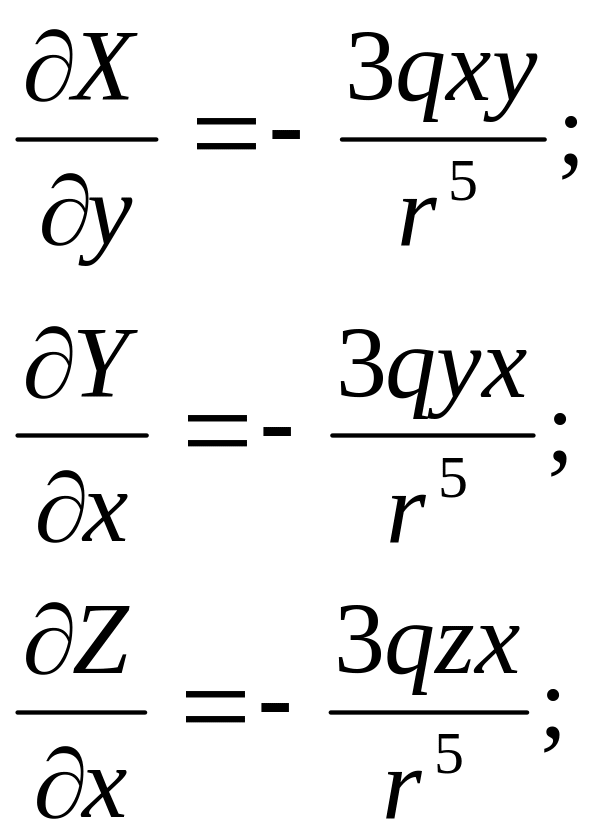
Следовательно,

т.е.

Отсюда следует, что поле напряженностей точечного заряда q потенциальное.