Московский Государственный Технический Университет имени Н. Э. Баумана.

Калужский филиал

«Кривые II порядка»

Учебно-методическое пособие.

ФН3-КФ

Составили: Королёва Т. В.

Боркина О. Н.

Рецензент: Логинов Б. М.

Калуга-2007 г.

1. Эллипс.

Определение:Эллипсом называется геометрическое место точек плоскости, для которых, сумма расстояний до 2-х фиксированных этой же плоскости, называемых фокусами эллипса, есть величина постоянная (=2а).

Вывод уравнения эллипса.

Выберем систему координат следующим образом:

И F_1,F₂– фокусы эллипса,

т. эллипсу.

F_1,F₂ – расстояние между фокусами эллипса.

Очевидно, что , так как2a– сумма 2-х сторон, а2с– его третья сторона.

Таким образом, по определению эллипса имеем:

(1)

Запишем это уравнение в координатной форме, заменив и, получим уравнение эллипса в данной системе координат:

(2)

Упростим его:

;

Разделим на:

Получим: (3)

Так как , то можно обозначить(4), то есть имеем простейшее (каноническое) уравнение эллипса:

(5)

Примечание 1.

Вообще говоря, надо доказать, что уравнение (5) есть уравнение данного эллипса, так как это уравнение получено из уравнения (2) двукратным освобождением от радикалов, очевидно лишь, что уравнение (5) есть следствие уравнения (2). Мы должны доказать, что уравнение (2) есть в свою очередь следствие уравнения (5), т.е. , что они эквивалентны.

Доказательство смотрите в учебнике Н. В. Ефимова (Краткий курс аналитической геометрии, М, 2005, стр. 72 (2-ой абзац сверху)- стр. 73) или в другом курсе аналитической геометрии.

Таким образом, уравнение (5):

Определяющее эллипс в некоторой системе координат декартовых прямоугольных, есть уравнение 2-ой степени относительно “x” и “y”.

Форма эллипса:

2. 

То есть

Таким образом, эллипс целиком лежит внутри прямоугольника, определяемого этими неравенствами.

2. Уравнение сохраняет вид, если “x” заменить на“-x”, а“y” заменить на“-y”.

Таким образом, оси координат x=0 ( осьOY) иy=0 ( осьOX) являются осями симметрии эллипса, следовательно, достаточно построить дугу эллипса, лежащую в первой четверти.

2. Построим эллипс в 1-ой четверти. Имеем 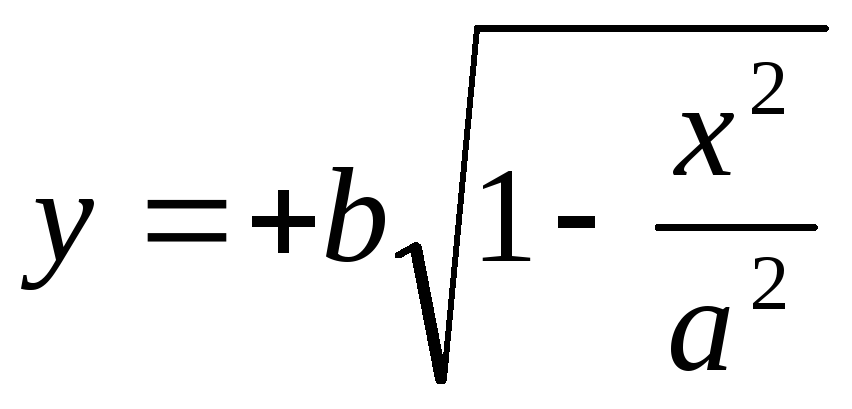- уравнение эллипса для первой четверти, при этом.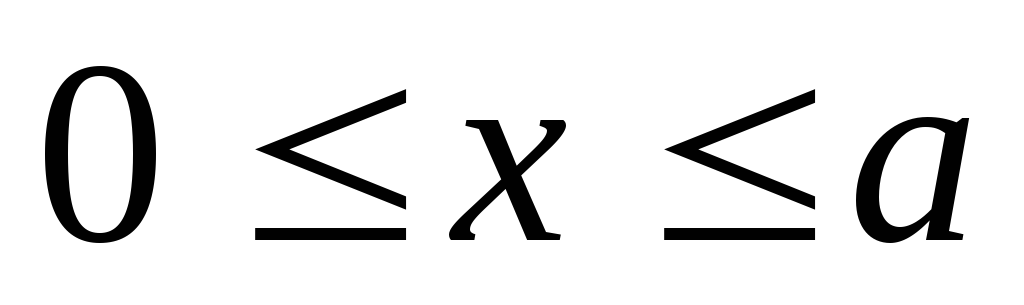

Или после преобразования ,.

Имеем при

При

Замечаем, что при возрастании “x”от“0”до”a”,“y”убывает от“0”до”b”.

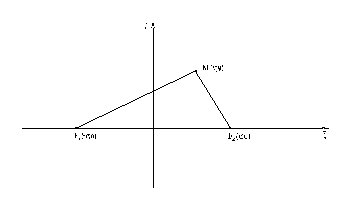
Строи кривую в 1-ой четверти.

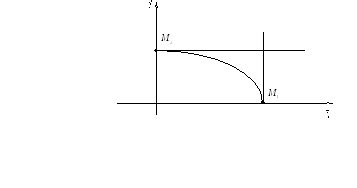
2. Строим эллипс.

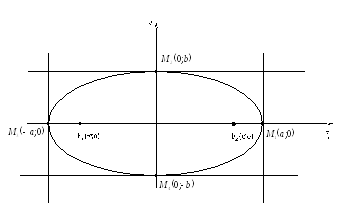
Точки М₁, М₂, М₃, М₄– вершины эллипса.

-большая ось (a– большая полуось).

-малая ось (b– малая полуось).

Так как . Точка пересечения осей симметрии называется центром эллипса (т.).

c-половина фокусного расстояния.

Имеем:

Замечание 1: приэллипс превращается в окружность радиусаи с центром в начале координат.

Эксцентриситет эллипса.

Для характеристики формы эллипса пользуются эксцентриситетом .

Определение: Эксцентриситетом эллипса называется отношение половины фокусного расстоянияк большой полуоси, т.е.

(6)

Т.к., то

.

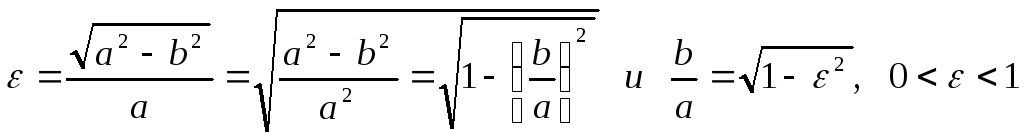Чем ближе к единице, тем меньше, следовательно, отношение, тем более эллипс вытянут вдоль осиOX. При,, следовательно,и эллипс превращается в сдвоенную большую ось. Чем больше, тем больше форма эллипса приближается к окружности.

При , имеем окружность, т.е. для окружности.

Замечание 2.

Рассмотрим уравнение эллипса , где, т.е.b- большая полуось,a– малая полуось. Для него.

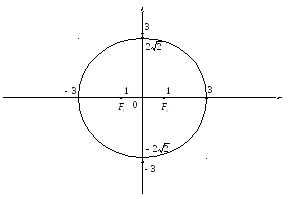
Примеры.

1. Построить кривую по уравнению и вычислить c, , построить фокусы

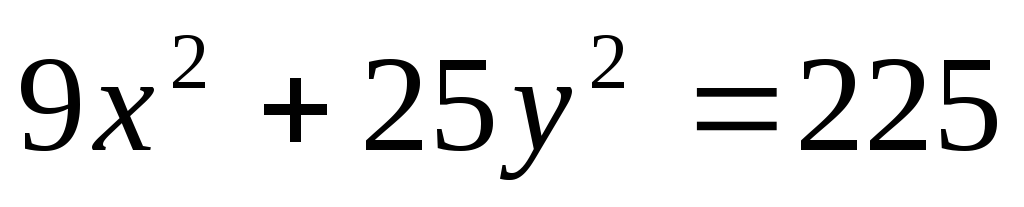
Решение:

, имеем:

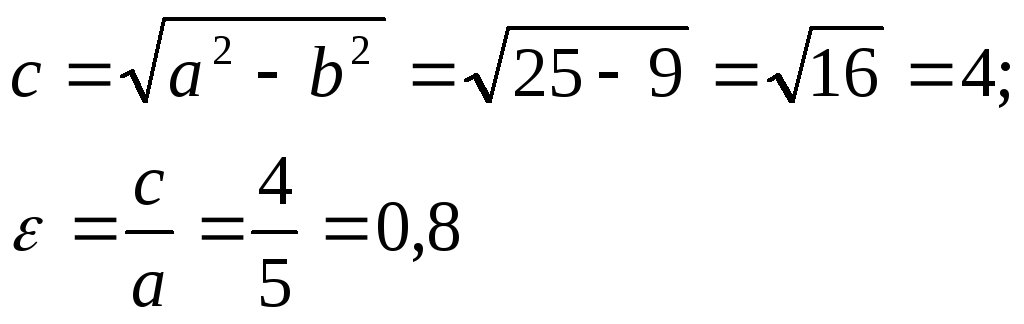
У этого эллипса центр находится в точке

2. Написать уравнение эллипса, для которого большая полуось 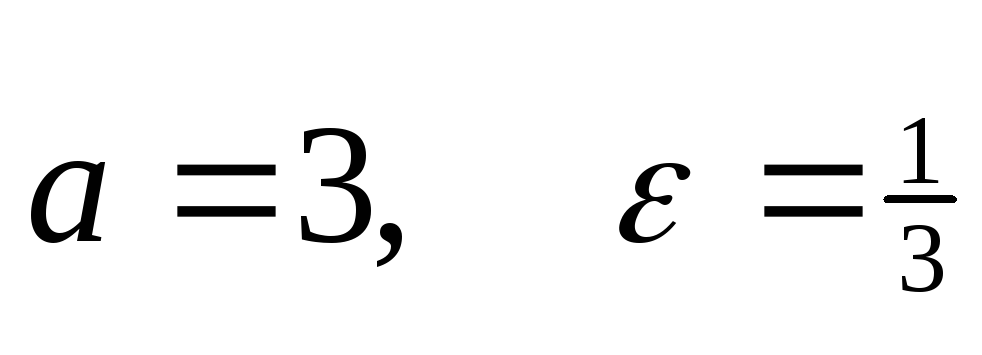, центр лежит в точкеи оси координат являются осями симметрии эллипса. Построить эллипс.

Решение:

Если , то, следовательноПолучим уравнение эллипса:.