ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение

высшего профессионального образования

Донской Государственный Технический Университет

Кафедра «Высшая математика»

УТВЕРЖДЕНО

проректором по учебной

работе

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям по теме:

«Криволинейные, поверхностные интегралы

и элементы векторного анализа»

Составители:

Доц., к.т.н. Тарасов Е.А.

доц., к.ф-м.н. Виноградова И.Ю.

ст. преп. Шевченко Н.П.

г. Ростов-на-Дону

2008

Часть 1

1. Криволинейный интеграл второго рода

Пусть на некоторой дуге кривой задана непрерывная функция , где - точка, лежащая на кривой . Разобьем дугу кривой на произвольных частей точками ; , (рис. 1).

Будем считать длина дуги , равной . На каждой из частей разбиения выберем произвольную точку и составим сумму:

,где проекция на ось . Эта сумма называется интегральной суммой для криволинейного интеграла второго рода, а предел этой суммы, если он существуют, при стягивании каждого из участников, при стягивании каждого из участков разбиения в точку называется криволинейным интегралом второго рода или криволинейным интегралом по координате и обозначается:

Если проектировать на оси и , то аналогично можно получить интегралы второго рода по координатам u

где и некоторые другие непрерывные функции, заданные на кривой . Введенные нами интегралы второго рода называются простейшими интегралами, а их сумма называется интегралом второго рода и обозначается:

. (1.1)

Если кривая есть пространственная кривая, то функции , , являются функциями трех переменных и интеграл (1.1) имеет вид:

. (1.2)

Если кривая лежит в плоскости , то , функции и являются функциями двух переменных и интегралом (1.1) имеет вид:

(1.3)

Интегралы (1.2) и (1.3) называются соответственно криволинейными интегралами второго рода по пространственной и плоской кривой.

Разорвем физический смысл интеграла второго рода. Пусть в каждой точке кривой задана сила , под действием которой материальная точка перемещается по кривой . Сила является векторной функцией точки , координаты которой , , являются скалярными функциями точки . Тогда выражение стоящей под знаком суммы в равенстве (1.1) является скалярным произведением значения вектора силы в точке на вектор пути , которое равно работе, затрачиваемой силой на перемещение точки из положения в положение , в предположении что сила на участке постоянна и равна . Вся сумма представляет собой приближенное значение работы на перемещение материальной точки из положения в положение вдоль кривой , а предел (криволинейный интеграл) есть истинное значение работы.

2. Связь криволинейных интегралов первого и второго родов. Специфическое свойство интеграла второго рода

Рассмотрим криволинейный интеграл второго рода по пространственной кривой

(1.4)

Координаты переменной точки кривой можно считать функциями длины дуги . При выводе формулы производной по направлению были получены значения производных этих функций, которые равны направляющим косинусам касательной к кривой в точке .

,

где углы образованные касательной к кривой в точке с осями , и .

С точностью до малых высшего порядка можно считать

Следовательно, интегральную сумму равенства (1.1) можно записать в виде

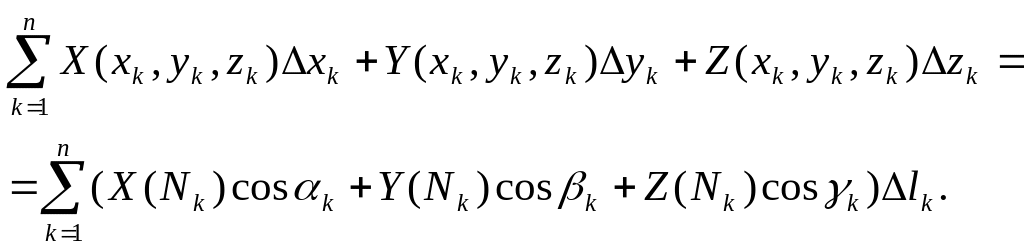
Правая часть полученного равенства является интегральной суммой для криволинейного интеграла первого рода по дуге кривой . Переходя к пределу в полученном равенстве при стягивании в точку получим связь между криволинейным интегралом первого и второго родов.

(1.5)

Из формулы (1.5) следует, что все свойства, доказанные для общего интеграла (в частности для криволинейного интеграла первого рода) справедливы и для криволинейного интеграла второго рода. Однако из формулы (1.5) видно, что криволинейный интеграл второго рода определен неоднозначно в силу неоднозначности определения направляющих косинусов, для того, чтобы придать интегралу второго рода единственное значение, задают направление касательной к кривой , т.е. направление движения по кривой. В этом случае интеграл второго рода записывается в виде:

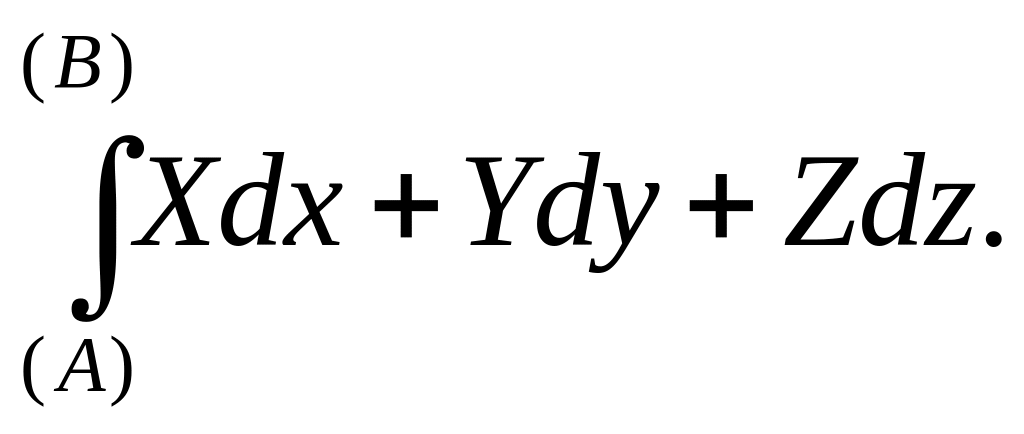
Если кривая замкнута, то вводят понятие положительного и отрицательного обхода замкнутого контура .

Определение. Положительным обходом замкнутого контура называется такой обход, при котором область, ограниченная этим контуром остается слева. В противном случае обход контура называется отрицательным.

В случае замкнутого контура криволинейные интегралы обозначаются

В связи с введенным понятием направления движения по кривой l на противоположное, то знак интеграла изменяется на обратный.

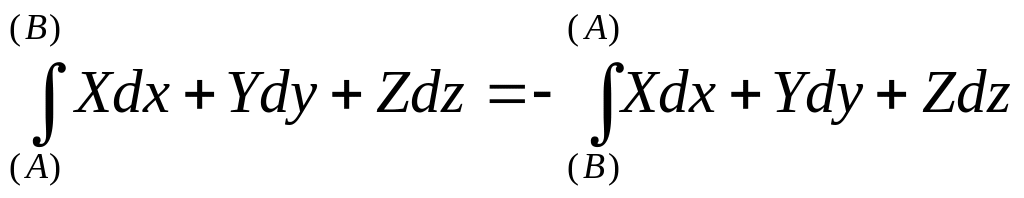
Справедливость этого свойства из формулы (1.5), так как при изменении направления движения, а, следовательно, и направления касательной все углы примут значения и направляющие косинусы изменят знаки.