Часть 2

ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА

Если в каждой точке пространства или части пространства определен вектор то говорят, что задано векторное поле. В координатной форме задание векторного поля равносильно заданию трех скалярных функций точки , так что

где – координаты точки .

10. Поток векторного поля

Пусть в некоторой области имеем векторное поле

причем непрерывны (поле непрерывно) в области . Рассмотрим поверхность , целиком лежащую в области . Пусть в каждой точке этой поверхности определен единичный вектор нормали

направляющие косинусы которого являются непрерывными функциями координат точки поверхности. Введем в рассмотрение поверхностный интеграл 1 рода по поверхности от

(2.1)

Если вектор рассматривать как скорость жидкости в точке , то интеграл (2.1) выражает количество жидкости, протекающей через поверхность в единицу времени. По этой причине его называют потоком векторного поля через поверхность .

Так как поверхностные интегралы 1 и 2 рода связаны между собой (см. (1.7)), то поток векторного поля можно выразить через поверхностный интеграл 2 рода:

Пример 1.

Вычислить поток вектора через часть плоскости , вырезаемой координатными плоскостями. За положительное направление нормали к плоскости принять то, которое образует острый угол с осью . П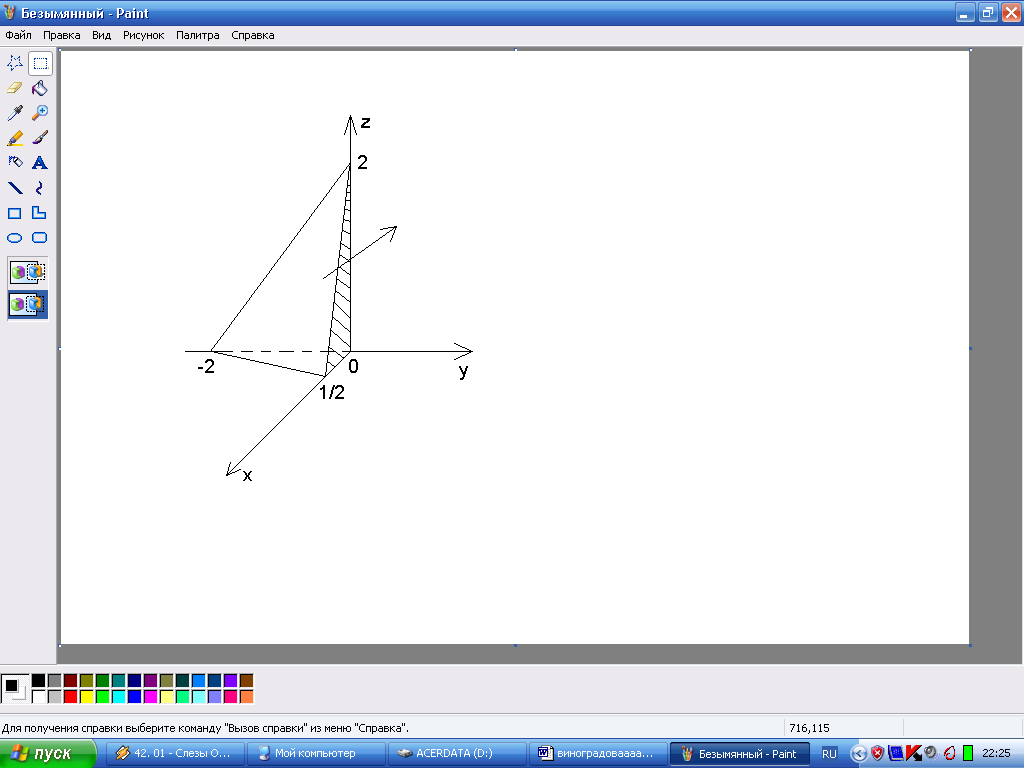 оток , где - единичный вектор нормали к данной плоскости, образующий с острый угол. Возьмем противоположный вектор {-4; 1; -1}, этот вектор перпендикулярен к данной плоскости и образует острый угол с осью , так как

Определим единичный вектор нормали, для этого найдем

и орт нормали

отсюда

тогда

Поток вектора :

н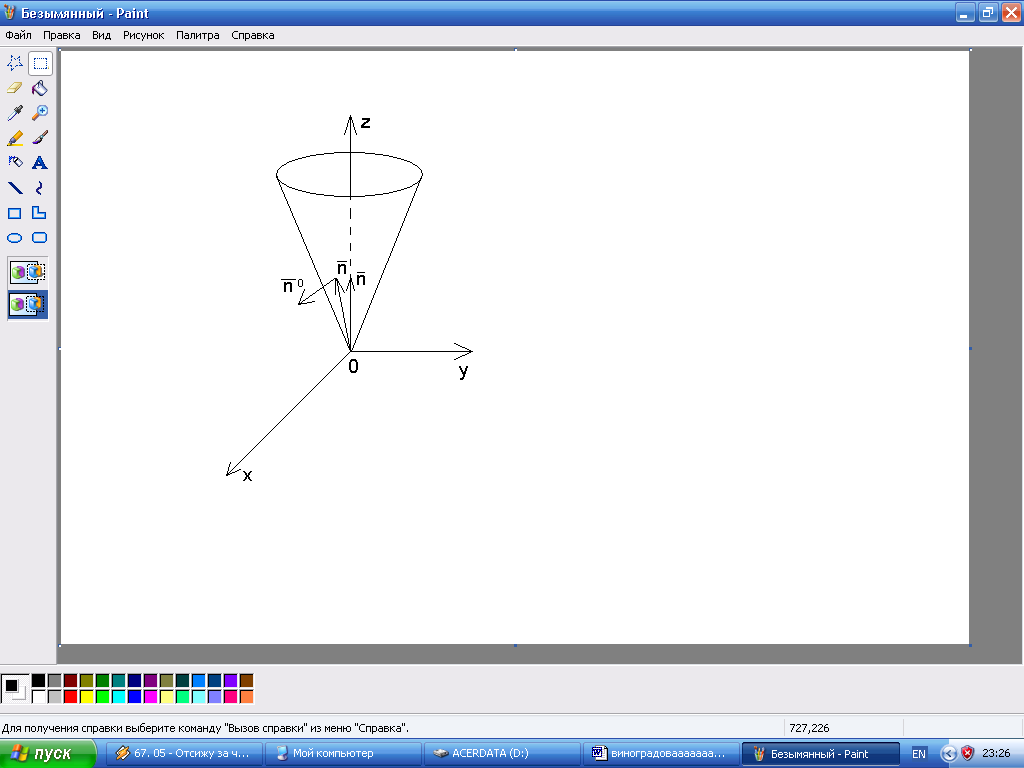 о

Перейдем от поверхностного интеграла к двойному, вместо подставим его значение из уравнения плоскости

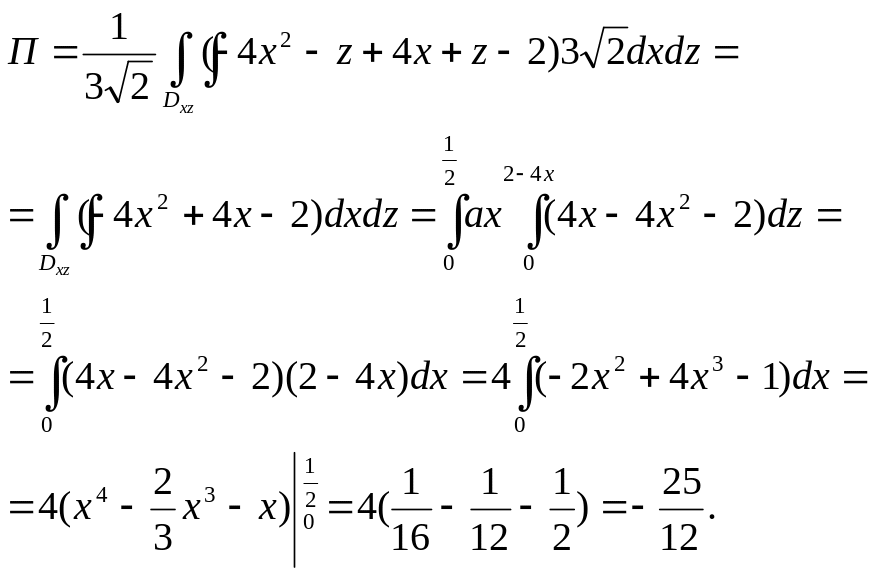
Пример 2.

Найти поток радиуса-вектора через внешнюю сторону поверхности прямого конуса, вершина которого совпадает с началом координат, если известны радиус основания конуса и его высота .

Поток вычисляется по формуле

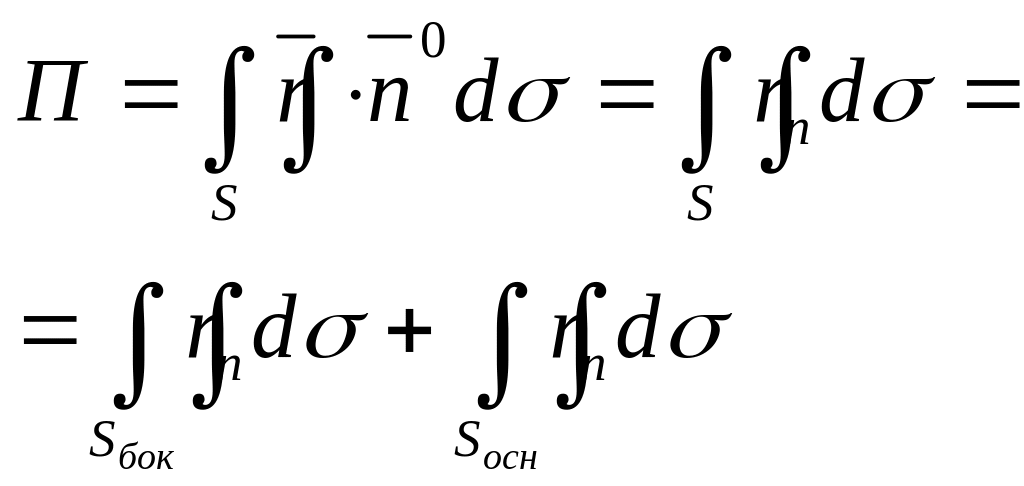
На боковой поверхности

На плоскости , поэтому

Поток через внешнюю сторону поверхности конуса

Ответ:

20.Поток вектора через замкнутую поверхность. Дивергенция векторного поля.

Если в некоторой области пространства функции непрерывны вместе со своими частными производными то по формуле Остроградского (1,9) поток векторного поля через любую замкнутую поверхность , расположенную в области , равен тройному интегралу от по области , ограниченной поверхностью .

(2.2)

Пример 3.

Тело Т лежит в первом октанте и ограничено плоскостями координат и поверхностью, заданной уравнением Вычислить поток поля вектора

Поток вычисляется по формуле

так как в данном случае

поверхность замкнута, то можно

применить формулу (2.2).

Имеем следовательно,

Таким образом, поток вектора вычисляется следующим образом

Для вычисления тройного интеграла перейдем к цилиндрическим координатам:

Уравнение параболоида . Следовательно,

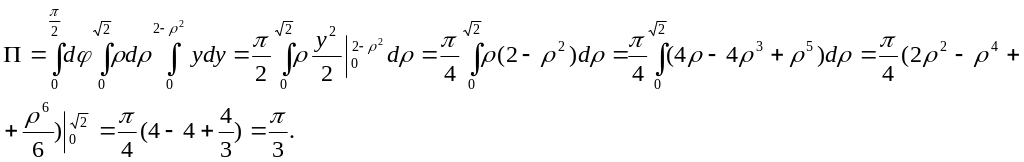
Дивергенцией векторного поля называется скаляр

С помощью определения дивергенции формула Остроградского в векторной форме примет следующий вид

(2.3)

т.е. интеграл от дивергенции векторного поля по некоторому объему равен потоку вектора через поверхность , ограничивающую данный объем.

Пример 4.

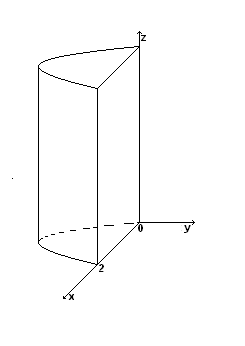
Найти поток вектора через внешнюю сторону поверхности цилиндра , ограниченного плоскостями

Решение:

найдем

Отсюда

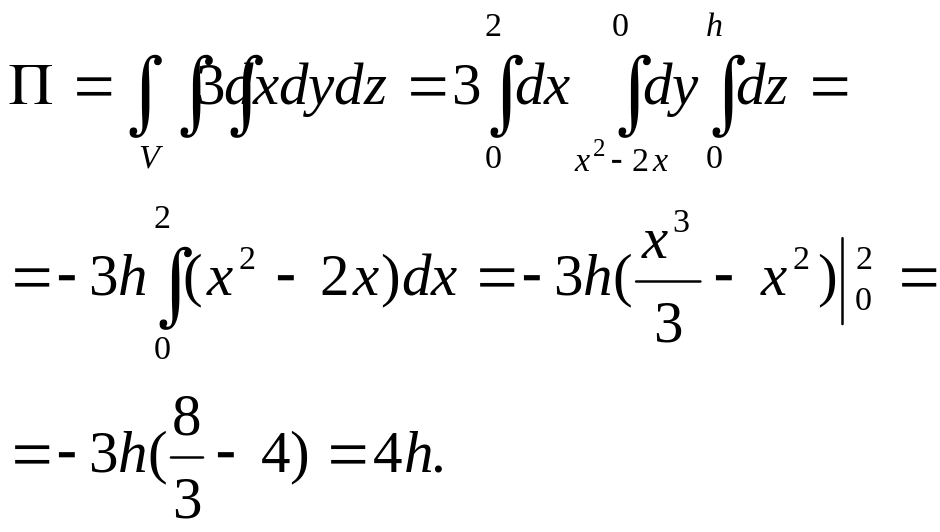
Ответ:

Пример 5.

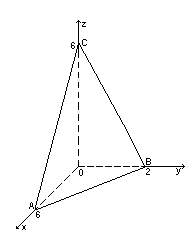
Плоскость образует с координатными плоскостями поверхность пирамиды. Вычислить поток поля вектора через поверхность пирамиды в направлении внешней нормали.

Решение:

Определим дивергенцию вектора

Тогда поток по формуле Остроградского

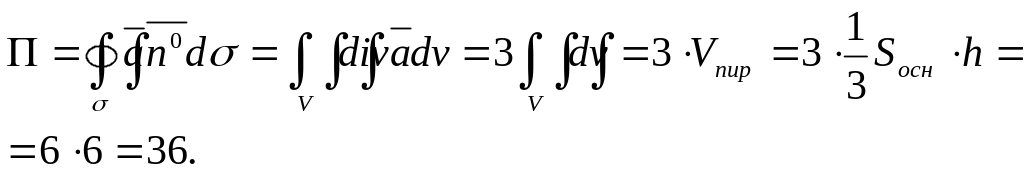
Ответ: .

Дивергенция дает количественную характеристику поля. Выясним её смысл. Из формулы (2.3) с помощью теоремы о среднем для тройного интеграла находим

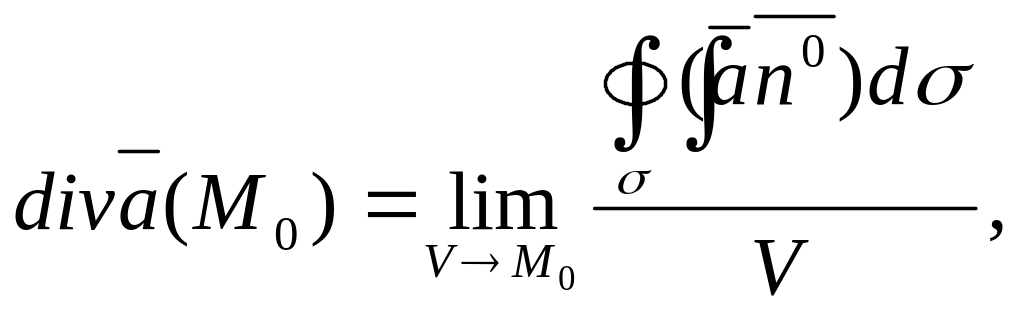(2.4)

где – любая точка области , - поверхность, окружающая , целиком лежащая в , – объем области, ограниченной поверхностью .

Формула (2.4) означает, что дивергенция поля в точке есть объемная плоскость потока вектора в этой точке.

Точки, в которых дивергенция положительна, называется источниками (в этом случае поток векторного поля через малую замкнутую поверхность, окружающую такую точку, положителен). Точки, в которых дивергенция отрицательная, называется стоками (в этом случае поток векторного поля через малую замкнутую поверхность, окружающую такую точку, отрицателен).