Криволинецные интегралы и теория поля

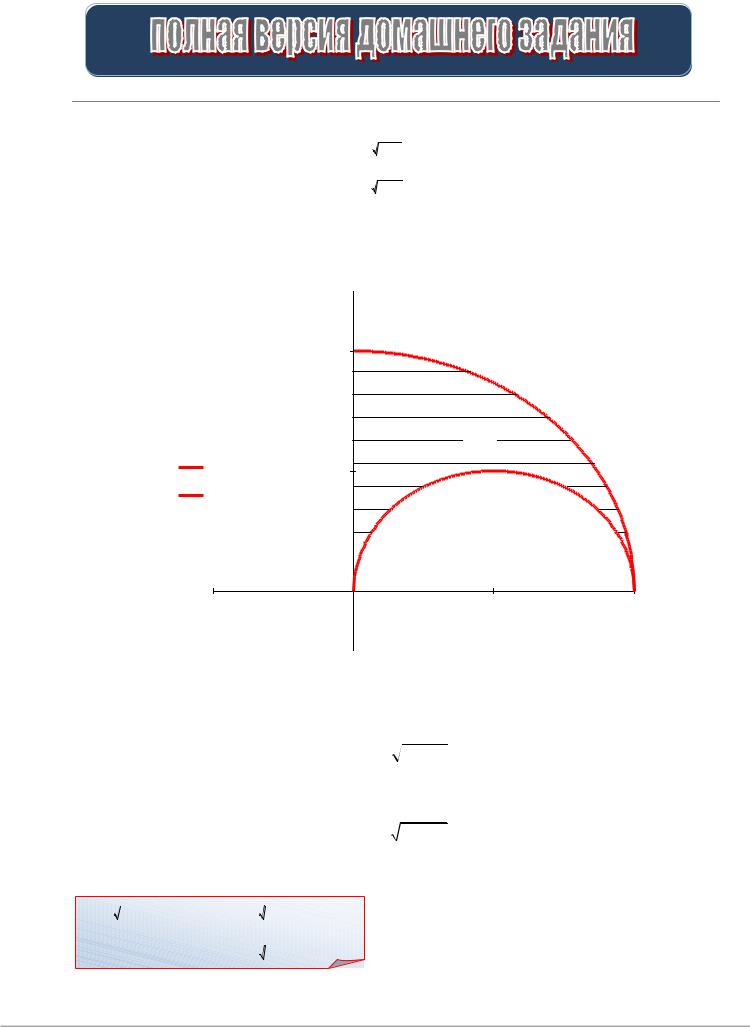
Задача 1.Изменить порядок интегрирования

Решение На рис.1 показана область интегрирования

Рис.2x

Данную область D можно представить как область, ограниченную графиком функции

y 16 x2

за вычетом области, ограниченной графиком функции

y 4x x2

при 0 y 4 , поэтому исходный интеграл равен

2

Задача 2. Вычислить объём тела, ограниченного поверхностями

x2 y2 z2 9 z 0

z 4

Решение:

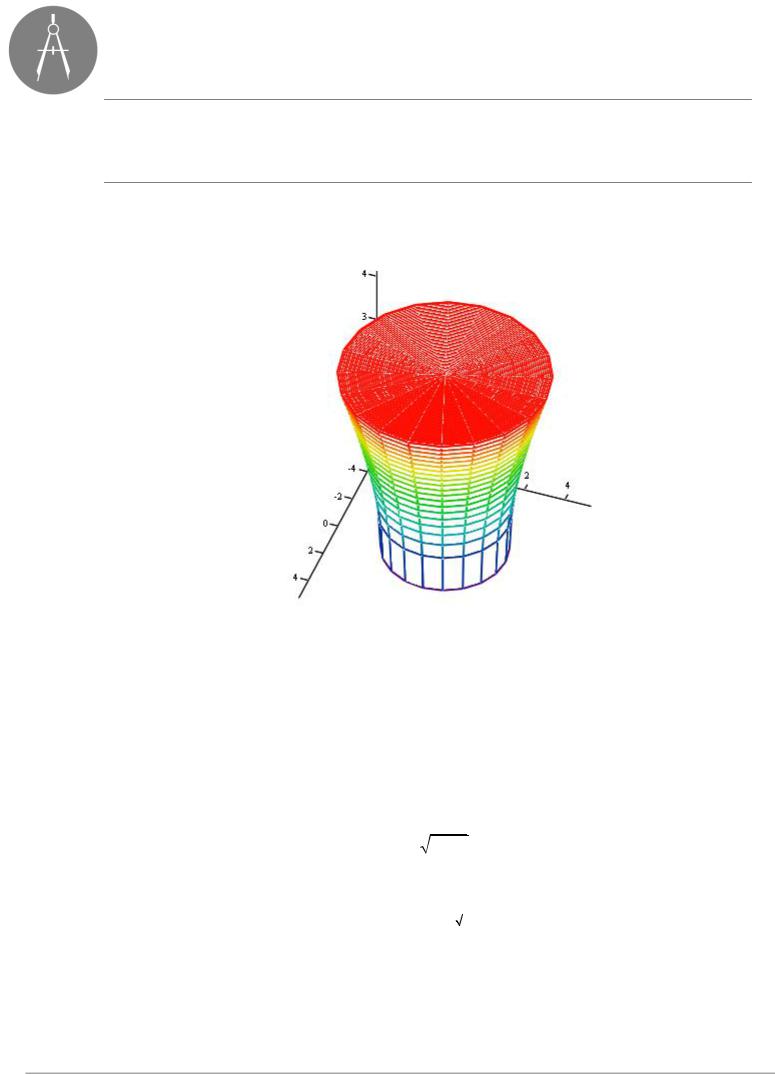
Тело, ограниченное данными поверхностями, показано на рис.3

Рис.3

Объём данного гиперболоида можно представить как разность объёмов цилиндра

(X Y Z) (X1 Y1 Z1)

r 5, 0 z 4

и тела между цилиндром и гиперболоидом, объём которого можно найти следующим образом.

Уравнение поверхности гиперболоида в цилиндрических координатах

z r2 9

Объём тела в цилиндрических координатах

вычислим его

Объём цилиндра равен

VЦ R2 H 52 4 100

Тогда объём гиперболоида равен

Ответ: V 272 3

5

В данном случае l M1M2 3; 1 ,

тогда производная функции в точке М1 по направлению к точке М2 равна

6

Направление наибольшего изменения скалярного поля – это всегда направление градиента, таким образом требуется найти градиент поля в точке М1

gradU (2;3) 4i 2 j

Величина изменения поля в точке М1 это соответственно модуль градиента в это точке

gradU 2;3 42 22 25

г) Работа вектора вдоль прямой – это криволинейный интеграл второго рода

д) Уравнение векторной линии градиента имеет вид

Так как необходимо найти уравнение векторной линии, проходящей через точку М0, то найдём постоянную С, подставив в уравнение координаты данной точки

ln1 1 C C 1 y 1 ln x искомое уравнение

y 1 ln x

7

Задача 4. В R3 задано векторной поле F x, y, z P x, y, z i Q x.y.z j R x, y, z k .

Найти: а) векторные линии поля; б) дивергенцию векторного поля и её значение в точке М0; в) поток векторного поля через границу S трёхмерной области V конечного объёма,

заданной пересечением поверхностей; г) поток векторного поля через поверхность ∑; д)

ротор векторного поля в произвольной точке; е) циркуляцию векторного поля по замкнутой линии L, образованной пересечением поверхностей (вычислить криволинейный интеграл непосредственно и проверить результаты по формуле Стокса).

Исходные данные:

Два последних уравнения определяют семейства цилиндрических поверхностей с образующими, параллельными осям Oz и Ox соответственно. Таким образом, векторные линии поля являются линиями пересечения данных поверхностей.

б) дивергенция поля

дивергенция поля в точке

divF M 1;1;2 1 1 2

в) трёхмерная область V представляет собой половину шара с центром в начале координат и радиусом 2.

Поток через границу данной области вычислим, используя формулу ОстроградскогоГаусса

9

Ротор в точке М(1;1;1) равен

1

x

Рис.7е.

Циркуляцию поля вдоль линии L можно представить как

Для вычисления последнего интеграла представим уравнение кривой АВ в параметрическом виде

y 2 cos t, y ' 2sin t z 2sin t, z ' 2 cos t x 0

0 t

2

тогда

Проверим вычисления с помощью формулы Стокса (в данном случае она вырождается в формулу Грина)

10

F l0 dl rotF n dG

L G

При расчёте циркуляции направление обхода было выбрано против часовой стрелки, поэтому нормаль к поверхности G имеет координаты n(1;0;0), а ротор поля имеет координаты (0;0;-x), их скалярное произведение равно нулю, поэтому циркуляция поля равна нулю.

F l0 dl 0

L

P.S.: готовы ответить на любые вопросы. Желаем успехов и побед!

UService