40. Формула грина
Установим связь между криволинейным интегралом по плоской кривой и двойным интегралом.
П
усть
в плоскости
задан замкнутый контур
,
ограничивающий плоскую область
,
которая ограничена кривыми
(кривая
),
(кривая
),
.
Пусть в области
заданы непрерывные функции, имеющие
непрерывные частные производные.
Рассмотрим интеграл
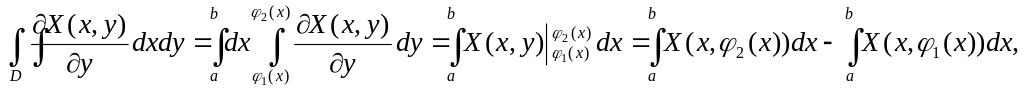
но
является криволинейным
интегралом по кривой
,
криволинейным интегралом по кривой
.
Следовательно:
Окончательно получим:
Аналогично можно получить:
Вычитая из второго первое равенство, получим:
(1.6)
Это и есть формула Грина.
Пример 6.
Вычислить вдоль
кривой
:
Решение:
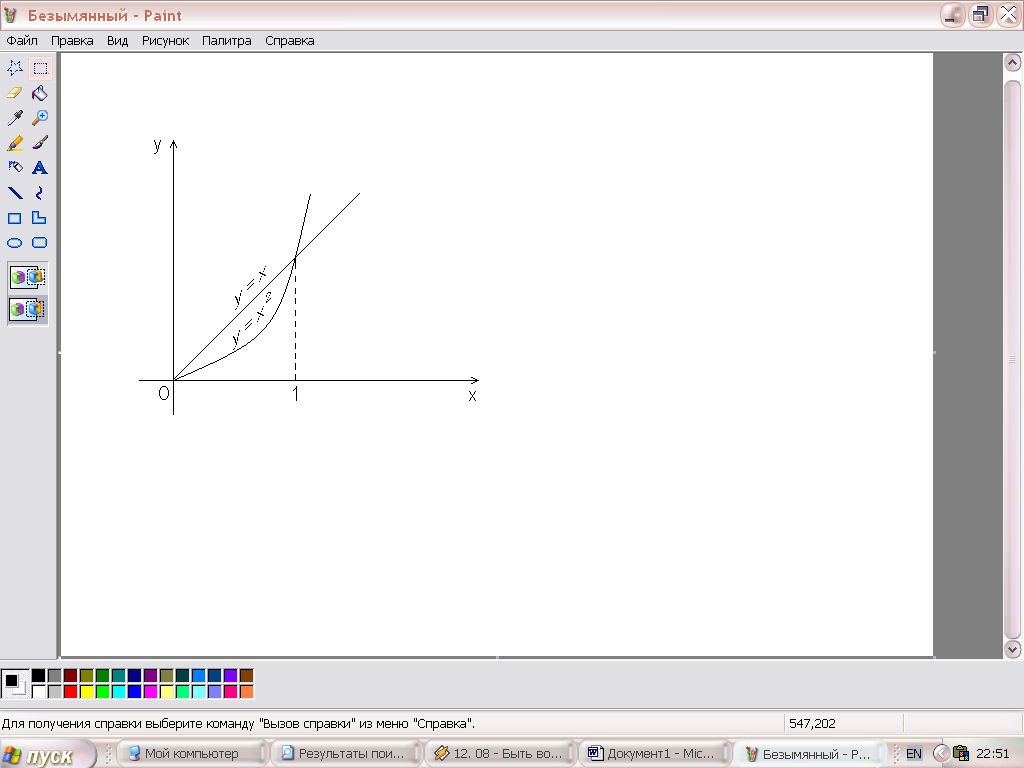
Пример 7.
Вычислить криволинейный интеграл
1.
вдоль ломаной линии
:
О(0;0),
З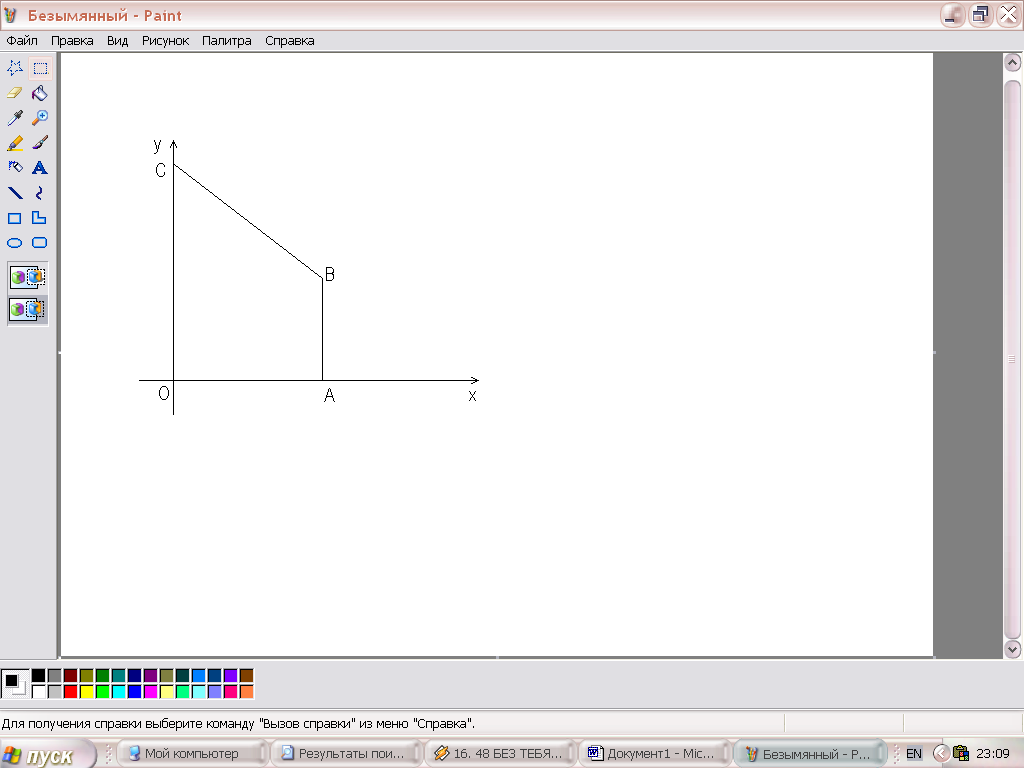
десь
линия интегрирования (замкнутая) состоит
из четырех отрезков, которые лежат на
различных прямых (с различными
уравнениями).
Поэтому криволинейный
интеграл по ломаной
вычисляем как сумму интегралов, взятых
по отрезкам
Уравнение
отсюда
.
Уравнение
Уравнение
Уравнение
,
преобразуем данный криволинейный
интеграл в обыкновенный с переменной
у и вычислим его:
Следовательно,
.
2. Так как контур интегрирования замкнутый, то для вычисления криволинейного интеграла можно применить формулу Грина:
50. Поверхностный интеграл 2-го рода
Как и криволинейный интеграл второго рода, поверхностный интеграл второго рода разбирается, в отличие от поверхностных интегралов по площади поверхности (первого рода) по направленной (ориентированной) поверхности. Ориентация поверхности осуществляется с помощью вектора нормали. Для любой двухсторонней поверхности в отличие от односторонней (например, лист Мебиуса) можно указать две ориентации вверх – вниз, внутрь – наружу и т.д.
Пусть дан кусок
двухсторонней поверхности
.
Выберем ориентацию поверхности, то есть
зададим вектор нормали в каждой точке
поверхности
Пусть
далее на поверхности
задана непрерывная функция
.
Разобьем поверхность
на
произвольных частей
и спроектируем каждую часть
на плоскость
.
Причем будем считать
положительной, если вектор нормали к
образует с осью
острый угол и отрицательной, если угол
тупой.
Составим сумму
,
где точка
принадлежит поверхности
.
Эта сумма называется интегральной
суммой для поверхностного интеграла
по переменным
,
а предел этой суммы, если он существует,
называется поверхностным интегралом
второго рода по координатам
и обозначается:
.
Аналогично можно
ввести поверхностные интегралы по
переменным
и
если спроектировать
на плоскости
.
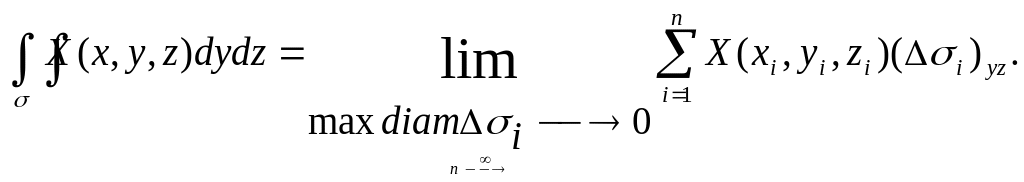
Необходимо заметить,
что как и
элементы площадей
могут иметь как положительный, так и
отрицательный знаки в зависимости от
углов, образованных вектором нормали
с осями
Сумма
простейших интегралов второго рода
называется составным поверхностным
интегралом второго рода
Установим связь между поверхностными интегралами первого и второго рода. Очевидно можно выразить следующим образом:
Пример 8.
Вычислить поверхностный интеграл
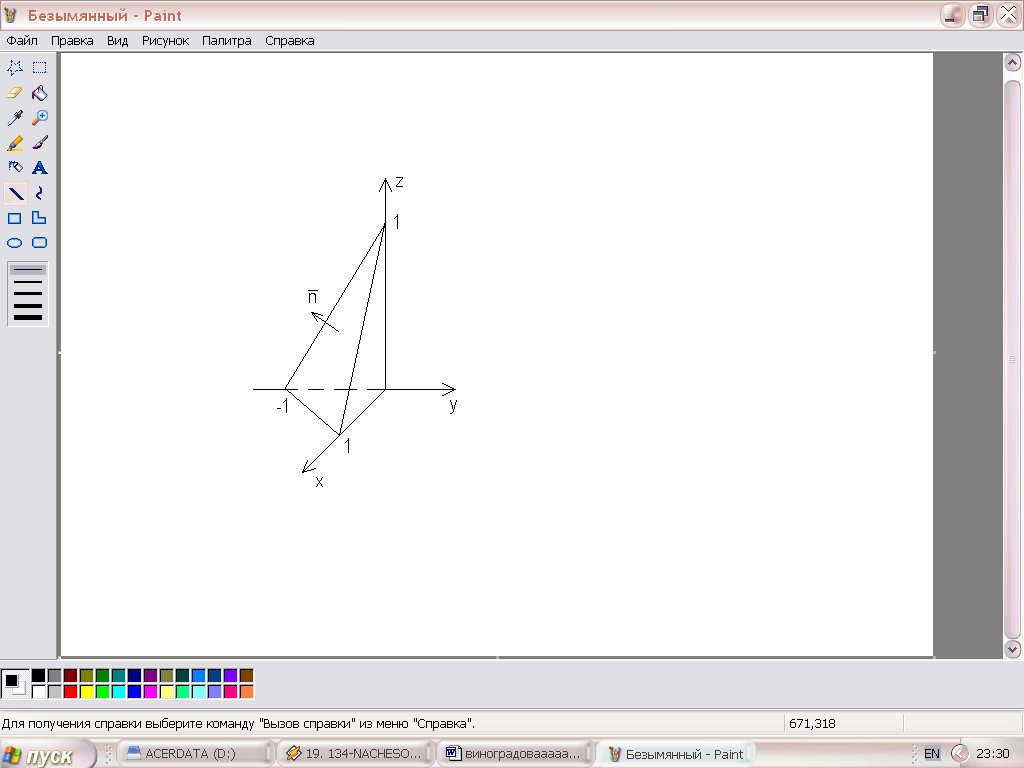
по внешней стороне
треугольника, ограниченного поверхностями
Решение:
Сделаем чертеж. Разобьем интеграл на сумму трех интегралов.
Вычислим интеграл:
.
Вектор нормали
образует
острый угол с осью
и следовательно в двойном интеграле
выбираем знак
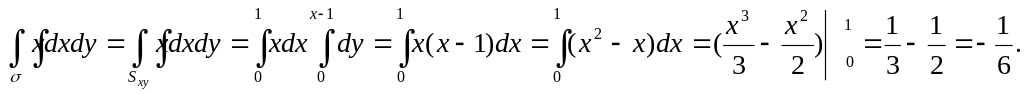
Вычислим
.
Угол, образованный вектором нормали
с
осью
тупой и
Следовательно нужно взять знак «минус»
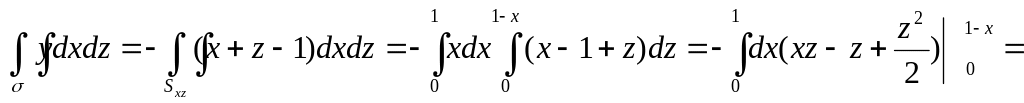
Вычислим
.
Угол между вектором нормали
и
осью
острый и следовательно нужно взять знак
.
Тогда интеграл второго рода преобразуется
в интеграл первого рода:
(1.7)
Подынтегральное
выражение второго интеграла формулы
(1.7) можно представить как скалярное
произведение векторной функции
с
координатами
и единичного вектора нормали
.
Тогда формулу (1.7) можно переписать в
виде
(1.8)
Из формулы (1.7) следует, что поверхностный интеграл второго рода обладает всеми свойствами общего интеграла. Однако, как и криволинейный интеграл второго рода поверхностный интеграл обладает специфическим свойством, связанным с ориентацией поверхности, справедливость которого следует также из формулы (1.7).
Свойство.
Если ориентацию поверхности изменить на противоположную, то знак поверхностного интеграла изменится на обратный.