
- •Тема 3. Переходные процессы в электроприводе.
- •Тема 3.
- •Тема 3. (ап )
- •3. Переходные процессы в электроприводе. Лекция 3.1. (5) (05.08.11)
- •3.1.6.1. Переходные процессы коммутации индуктивности.
- •1. Электромагнитные переходные процессы.
- •2. Электромеханические переходные процессы.
- •3. Тепловые переходные процессы.
- •Классический метод.
- •Операторный метод.
- •Частотный метод,
- •3.1.2. Классический метод анализа переходных процессов
- •3.1.2.1. Переходные процессы коммутации индуктивности.
- •1. Включение индуктивности в цепь постоянного тока.
- •3.1.2.2. Переходные процессы при коммутации емкости.
- •1. Включение емкости в цепь постоянного тока.
- •3.1.3. Операторный метод расчета переходных процессов.
- •3.1.3.1.Свойства преобразования Лапласа:
- •3.1.3.2. Законы Кирхгофа в операторной форме. [Сергеев в.В.]
- •3.1.3.3. Закон Ома в операторной форме.
- •Передаточная функция.
- •3.1.3.5. Теорема разложения.
- •3.1.4. Основные виды воздействующего сигнала.
- •3.1.5. Основные характеристики передаточного звена.
- •3.1.5.1. Переходная функция
- •3.1.5.2 Импульсная переходная функция. Функция веса.
- •3.1.6. Операторный метод анализа переходных процессов.
- •3.1.6.1. Переходные процессы коммутации индуктивности.
- •1. Включение индуктивности в цепь постоянного тока.
- •3.1.6.2. Колебательное звено второго порядка.
- •3.1.7. Частотный метод расчета переходного процесса. [Новгородцев 30 лекций по тоэ]
- •3.1.8. Уравнения типовых звеньев.
- •1. Идеальное интегрирующее звено.
- •2. Идеальное дифференцирующее звено.
- •3.1.9. Способы соединения звеньев.
- •Тема 3 (а-эр. Ок-эр)
- •3 . Переходные процессы в электроприводе. Лекция 3.2. (а-эр. Ок-эр)
- •3.2. Электромеханические переходные процессы в линейной системе привода без учета электромагнитной инерции двигателя.
- •3.2.1. Общие положения.
- •3.2.2. Электромеханические переходные процессы в линейной системе привода.
- •1. Анализ переходного процесса пуска.
- •3.2.3. Передаточная функция линейной системы привода без учета электромагнитной инерции двигателя.
- •3.2.4. Передаточная функция механической системы.
- •3.2.5. Электромеханические переходные процессы в нелинейной системе привода.
- •1. Анализ переходного процесса пуска.
- •2. Кривая разгона двигателя.
- •3.2.6. Cинтез переходного процесса.
- •4.5. Двухмассовая механическая система.
- •2.1 Общие сведения
- •3.2.7. Двух массовая механическая система.
3.1.5.2 Импульсная переходная функция. Функция веса.
Импульсной переходной функцией называется функция w(t), описывающая переходный процесс в системе при воздействии, представляющем собой дельта-функцию - (t).
1. Импульсная переходная функция w(t) определяется как обратное преобразование Лапласа от передаточной функции.
2. Передаточная функция может быть определена как преобразование Лапласа от импульсной переходной функции,
3. Импульсная переходная функция является производной от переходной функции.
w(t) = h'(t)
4. Переходная функция является интегралом от импульсной переходной функции.
1
h(t) = w(t) dt
0
АЭП. 3.1.22. 05.08.11. 02.10.11. 10.10.11.
3.1.6. Операторный метод анализа переходных процессов.
Поскольку для операторных токов, напряжений и сопротивлений справедливы законы Ома и Кирхгофа, то расчет операторных токов и напряжений будет аналогичным расчету постоянных токов и напряжений в резистивных цепях постоянного тока.
В частности, могут быть использованы все известные методы расчета (метод эквивалентных преобразований, метод узловых напряжений и т.д.), которые основаны на законах Ома и Кирхгофа.
Учитывая изложенное, приведем методику решения задач операторным методом.
Определяются начальные условия
 и
и
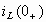 обычным
путем на основании законов коммутации.
обычным
путем на основании законов коммутации.
Для цепи после коммутации составляется операторная схема замещения, в которой элементы представляются их операторными схемами замещения, реальные токи и напряжения заменяются операторными. Такой замене подвергаются как искомые токи и напряжения, так и известные токи и напряжения источников.
Для операторной схемы замещения определяются искомые операторные токи и напряжения с использованием законов Ома, Кирхгофа и всех методов расчета (эквивалентных преобразований, эквивалентного генератора, узловых напряжений и т.д.).
По найденным операторным токам и напряжениям определяются реальные токи и напряжения по таблицам или по формуле разложения, которая рассмотрена выше.
Необходимо отметить, что при расчете переходных процессов операторным методом мы будем иметь дело с алгебраическими операциями над простейшими функциями переменного “р” каковыми являются операторные сопротивления и операторные функции источников (см. таблицу 3.1).
3.1.6.1. Переходные процессы коммутации индуктивности.
1. Включение индуктивности в цепь постоянного тока.

Рисунок 3.1.1. Коммутация индуктивности.
АЭП. 3.1.23. 05.08.11. 02.10.11.
Согласно второму закону Кирхгофа, используя операторную схему записи можно написать:
U = ur + ul = ir + L di/dt = i * R + L * i * p = i * (R + L * p)
Или
i = U / (R + L * p)
Если уравнения составлены при нулевых начальных условиях, то символ р можно рассматривать как алгебраическое число.
При анализе систем автоматического управления приводом их разбивают на звенья, на вход которых подается сигнал Нвх, а на выходе мы имеем преобразованный сигнал Нвых.
Звено изображается в виде структурной схемы. Структурная схема рассматриваемого звена приведена на рисунке 3.3.


Рисунок 3.1.3. Структурная схема апериодического звена.
Согласно схеме рис.3.1. Нвх = U.
Hвых = ur = i * R = U * R / (R + L * p)
W(p) = u2 / U = 1 /(Тe * р + 1 )
Где Тe =L/R
Рассматриваемое звено называется апериодическим звеном.
Переходная функция звена в операторном виде определяется делением его передаточной функции на р.
h(t) = 1/[p*(T*p+1)]
Согласно таблицы изображение – оригинал
/ [p*(p+)] (1- e -*t)
АЭП. 3.1.24. 05.08.11.
Где = 1/Т
Переходная функция звена это результат воздействия 1(t) , т.е. в нашем случае результат воздействия на схему напряжения в 1 Вольт.
При подаче напряжения в U B
U2 = U*(1+e- t/T)
Этот результат получен ранее классическим методом.
Аналогично можно получить переходную функцию и для включения емкости на постоянное напряжение.
