6. Метод наложения

Используя метод наложения определим один из токов ветвей для заданной электрической цепи. Величины параметров элементов цепи приведены в табл. 3. Схема цепи – на рисунке 6.1.

Таблица 3

Определяемый ток	Величины параметров элементов цепи
	E1, В	E2, В	J1, A	J2, A	R1, Ом	R2, Ом	R3, Ом
I2	10	0	1	0	10	10	10

I₂

I₃

(0)

I₁

J₂

R₂

R₃

R₁

E₁

Рис. 6.1 Схема цепи

а)

б)

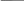
R₂

R₁

R₂

R₃

R₁

E₁

J₁

Рис.6.2

Ток можно представить в виде суммы двух частичных токов I₂^Е и I₂^J1, вызванных действием источника напряжения и источника тока . Схемы замещения для расчета частичных токов приведены на рис. 6.2 а, б.

Используя закон Ома для цепи (рис.6.2,а), найдем частный ток

А

Частный ток третьей ветви равен току источника тока (по определению идеализированного источника тока, ток ветви задается током источника тока). Токи первой и второй ветви (параллельные ветви) распределяются обратно пропорционально их сопротивлением, следовательно, частный ток от действия источника тока равен

А

Суммируя частные токи второй ветви, получим искомый ток

=1 А

Вывод: Методом наложения определили ток I₂ для заданной электрической схемы. В основе метода наложения лежит принцип суперпозиции (наложения), линейных электрических цепей.

7.Метод эквивалентного источника.

Найдём методом эквивалентного источника ток в любой ветви без источника. Электрическая схема представлена на рисунке 7.1.

Рис. 7.1.

Разомкнем ветвь с и определим для 3 контура рисунок 7.2.

Рис. 7.2

Второй закон Кирхгофа для третьего контура запишется в виде:

Найдём ток . Запишем для 1 и 2 контуров уравнения по второму закону Кирхгофа:

для первого контура

для второго контура

Уравнения записанные по 1 закону Кирхгофа:

для первого узла

для второго узла

Компонентные уравнения:

для первой ветви

для второй ветви

для третьей ветви

для четвертой ветви

для пятой ветви

Компонентные уравнения подставляем в уравнения, составленные по 2 закону Кирхгофа, а уравнения составленные по 1 закону Кирхгофа, оставляем без изменений:

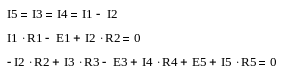
Решив данную систему, найдём ток

Эквивалентное сопротивление определяется из схемы рис 7.3.

Рис. 7.3.

Эквивалентное сопротивление:

Подставив данные значения сопротивлений, получаем:

;

Находим напряжение , которое равно:

Ток первой ветви на сопротивлении найдём, как:

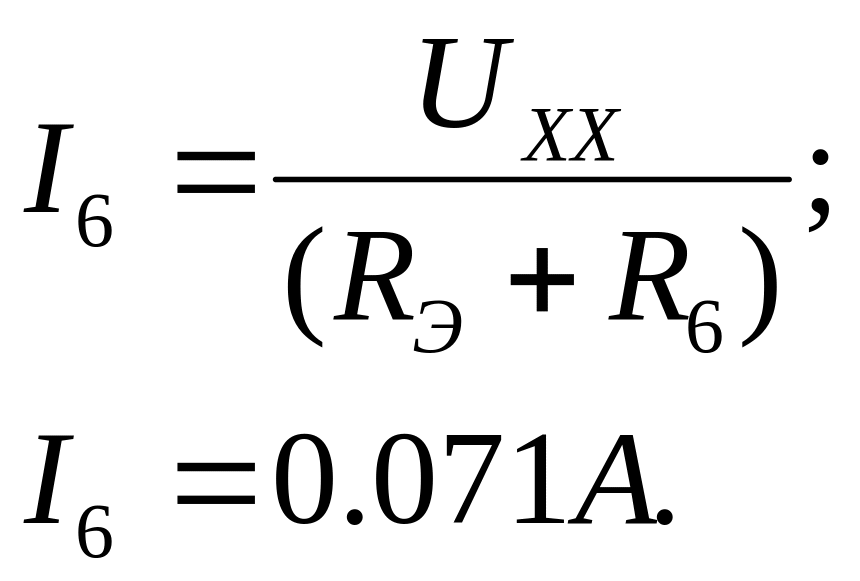
Вывод: Метод эквивалентного источника базируется на теореме об активном двухполюснике и позволяет упростить решение многих задач, связанных с передачей сигналов и электрической энергии от источника к приёмнику. Методы эквивалентного источника как напряжения и тока дают один и тот же результат. Применение того или иного метода определяется удобством и простотой нахождения или .