
- •Министерство образования Российской Федерации
- •1. Элементы теории графов.
- •1.1. Основные понятия теории графов
- •1.2. Способы задания графов
- •1.3. Связность графов
- •1.4. Изоморфизм графов
- •1.5. Планарные графы
- •1.6. Эйлеровы графы
- •1.7. Гамильтоновы графы
- •1.8. Деревья
- •Контрольные вопросы
- •2. Задачи и алгоритмы
- •2.1. Алгоритмы поиска
- •2.2. Раскраска в графах
- •2.3. Алгоритмы построения деревьев
- •2.4. Алгоритмы поиска путей
- •2.4.1. Алгоритм Дийкстры
- •2.4.2. Алгоритм Форда
- •2.4.3. Алгоритм Флойда
- •2.5. Потоковые алгоритмы
- •2.5.1. Определения и постановки задач
- •2.5.2. Алгоритм поиска максимального потока
- •2.5.3. Алгоритм поиска потока минимальной стоимости
- •2.5.4. Динамический поток
- •2.5.5. Алгоритм дефекта
- •Контрольные вопросы
- •3. Задачи для самостоятельного решения
- •4. Литература
- •Содержание
Марийский
Госдарственный Технический Университет
Учебное
пособие
Н.
В. Костромина Б. Л. Истомин
Графы:
теория, задачи, алгоритмы
Йошкар-Ола, 2000г
ББК
K
УДК
Рецензенты:
1.
2.
Печатается
по решению редакционного издательского
совета МаГТУ.
Н. В. Костромина,
Б. А. Истомин. Теоретические
основы применения графов: Учебное
пособие.-Йошкар-Ола, МарГТУ, 2000.- с
Приведены
основные понятия теории графов,
специализирующихся в области прикладной
математики, информатики и вычислительной
техники.
Костромина Н. В., Истомин Б. А.
Мариский Государственный
Технический Университет
Введение
Теорию
графов начали разрабатывать для решения
некоторых задач о геометрических
конфигурациях, состоящих из точек и
линий. В этих задачах несущественно,
каким видами линий (дугами, прямыми) и
какой длины соединены точки конфигурации,
а важно лишь то, что каждая линия
соединяет какие либо две из заданных
точек.
Таким
образом, граф можно представить как
совокупность двух множеств: V-
(точек) и U
- линий, между элементами которых
определено отношение инцидентности,
т.е. каждый элемент uU
инцидентен ровно двум элементам v1,v2V
(или каждая вершина инцидентна какому-
либо ребру); G
= < V, U >.
Элементы
множества V
называются вершинами (или узлами) графа
G,
элементы множества U-
его рёбрами. Вершины и рёбра графа
называют также его элементами и вместо
vV
и uU
пишут vG,
uG.
.
Первая
работа по графам была опубликована в
1736 г. Леонардом Эйлером. Эта работа
объясняла решение задачи о кенигсбергских
мостах: можно ли совершить про-
а)
б)
Рис. В1 гулку
по городу, чтобы, выйдя из любого места,
вернуться в него, пройдя только один
раз по любому мосту?
Ясно,
что по условию задачи не имеет значения,
как проходит путь по частям суши a,
b,
c,
d,
на которых расположен город, поэтому
их можно представить вершинами. А так
как связи между частями суши осуществляются
только через семь мостов, то каждый из
них изображается ребром, соединяющим
соответствующие вершины. В результате
получается граф, показанный на рис. В.1
Исследуя этот граф, Эйлер дал отрицательный
ответ на свой вопрос, более того, он
доказал, что подобный маршрут имеется
только на таком графе, каждая из вершин
которого связана с чётным числом рёбер.
В
середине XIX
в. Г. Кирхгоф применил графы для анализа
электрических цепей. Как математическая
дисциплина, теория графов сформировалась
к середине 30-х годов XX
века, её основатели: Д. Кениг, Л. С.
Понтрягин, А. А. Зыков, В. Г. Визинг и др.
С помощью теории графов, наряду с
головоломками и играми, решаются многие
важные практические задачи, в которых
имеется некоторое множество объектов,
тем или иным образом связанных друг с
другом. Это могут быть сети автомобильных
дорог, телефонные и другие коммуникационные
сети, системы нефтепроводов и т. п.
Теория
графов, как раздел дискретной математики,
успешно применяется в задачах управления
производством и при проектировании
сетей ЭВМ, при разработке современных
электронных модулей и при проектировании
физических систем с сосредоточенными
параметрами, при решении задач
автоматизированного проектирования.
Теория графов является основой
математического обеспечения современных
систем обработки информации.
Пусть V={v1,…,vN}– произвольное конечное множество
элементов, аU={u1,…,uR}– множество элементов, каждый из которых
представляет собой пару элементов
множестваV:
uk=(vi,vj).Тогда совокупность обоих множествG=<V,U>называется графом. Элементы множестваVназываются вершинами
(узлами) графа, элементы множестваU– ребрами графа, причем еслиuk=(vi,vj),
то вершиныviиvjинцидентны ребруuk,
а реброukинцидентно вершинамviиvj.
Две вершины, инцидентные одному ребру,
или два ребра, инцидентные одной вершине,
называются смежными или сосудними.
Понятие смежности относится только к
однородным элементам графа (вершинам
или ребрам) в отличие от понятия
инцидентности, относящемуся к неоднородным
элементам. Рис.
1.1
Ребро
uk=(vi,vj)
называется ориентированным (направленным),
или дугой, если вершины vi
и vj
являются упорядоченными, в противном
случае ребро называется неориентированным.
Дуга- это направленное ребро, она имеет
начало и конец. Началу соответствует
первая по порядку вершина, инцидентная
данной дуге, а концу – вторая.
Если
все рёбра графа являются направленными,
граф называется ориентированным или
орграфом (рис. 1.1). Если все рёбра графа
ненаправлены, граф называется
неориентированным или неографом. Граф,
содержащий как ребра, так и дуги,
называется смешанным. Смешанный граф
может быть получен из орграфа заменой
кратных дуг с противоположной ориентацией
ребром.
Если
две вершины графа соединяются более
чем одной дугой (ребром), то такие дуги
(ребра) называют кратными (или
параллельными), а сам граф называется
мультиграфом. Ребро, соединяющее вершину
графа саму с собой, называется петлей.
Граф
без петель и кратных ребер называется
простым или обыкновенным. Рис. 1.2
Если
в графе нет рёбер (U=),
то он называется пустым или нуль-графом.
Если в простом графе все вершины попарно
соединены рёбрами, то граф называется
полным.
Если множество вершин графа Vможно разбить на два подмножестваV1иV2 ,
которые не пересекаются и никакие две
вершины подмножестваV1иV2 не связаны между собой, граф называется
двудольным или биграфом (рис. 1.2).
Граф называется взвешенным, если его
элементам приписаны количественные
характеристики. В простейшем случае
ребру может быть приписан вес в виде
длины ребра, а вершине в виде степени
её значимости. Маршрутом
в графе называется последовательность
вершин и ребер (v1,u1,v2,u2,…,vn,un,vn+1)такая, что реброukинцидентно вершинамvkиvk+1.
Цепью называется маршрут, в который
каждая вершина входит не более одного
раза. Другими словами, цепь – это
несамопересекающийся маршрут. На рис.
1.3 (v6,u6,v3,u3,v4,u5,v5)- цепь,но(v6,u6,v3,u3,v4,u4,v1,u1,v2,u2,v3,u3,v4,u5,v5)– маршрут.
Рис. 1.3 Цепь
называется путем, если каждое ее ребро
ukлибо не ориентировано, либо ориентировано
в направлении отvkкvk+1.
Замкнутая цепь называется циклом.
Замкнутый путь, называется контуром.
На
рис. 1.3 вершины (v2,v1,v4,v3)
с соответствующими ребрами образуют
цепь, но не путь, (v3,v4,v5)
– путь, (v1,v4,v3,v2,v1)
– цикл, но не контур, (v1,v2,v3,v4,v1)
– контур.
Частью
G
графа G=<V,U>
такой, что G=<V,U>
и VV,
UU,
называется граф, вершины и рёбра которого
являются подмножеством вершин и рёбер
данного графа. Различают несколько
видов частей графа.
Подграфом
называется часть графа, содержащая его
некоторые вершины и рёбра.
Суграфом
называется часть графа, содержащая все
его вершины, но не все рёбра. Часть
графа, не вошедшая в подграф, называется
его дополнением.
Граф
по отношению к подграфу называется
надграфом.
Степенью
вершины i
неографа (обозначается deg(i)
) называется число, равное количеству
ребер, инцидентных данной вершине. Для
орграфа соответственно вводится понятие
полустепень исхода и захода: количество
исходящих и заходящих дуг для данной
вершины.
Расстоянием между вершинами viиvjd(vi,
vj)называется количество ребер в минимальной
цепи, соединяющей эти вершины. Как и
всякая метрическая величина,dобладает следующими свойствами: d(vi,
vj)=d(vj,
vi); d(vi,
vj)
0 , d(vi,
vj)=0,
если vi=
vj; d(vi,
vj)+d(vj,
vk)
d(vi,
vk),
- правило треугольника.
Вершина
графа называется его центром, если
максимальное расстояние от нее до
остальных вершин минимально из всех
возможных.
То есть
Вершина, для которой r(v)=R(G),называется центром графаG.
Пример:
Для
графа G
на рис.
1.4:
D(G)=3;
r(v1)=3;
r(v2)=2;
r(v3)=2;
r(v4)=2;
r(v5)=3.
R(G)=2,
то есть
v2,
v3
и v4
–центры G.
Операции над графами
Удаление
вершины v
или ребра u
графа, также переход к подграфу – это
операции, с помощью которых можно
получить граф с меньшим числом элементов.
Однако известны операции, позволяющие
получать графы с большим числом
элементов. Добавление
ребра: если вершины vi
и vj
не смежны, то можно построить граф G+u,
где u=(vi,
vj). Объединение:
граф H
называется объединением (или наложением)
графов F
и G,
если VH=VFVG
и UH=UFUG.
Пишут H=GF
(рис. 1.6)
Объединение
GF
называют дизъюнктивным, если VF*VG=
(рис. 1.5)
Рис
1.5
Рис
1.6 Рис.
1.7. Пересечение.
3.
Пересечением графов G
и F
называется граф H
такой, что VH=VFVG,
UH=UFUG.
Обозначается:
H=GF
4.
Произведением G1G2=G
называется граф, для которого VG=V1V2
- декартово произведение множеств
вершин исходных графов, а UG
строится так: вершины (v11,
v12)
и (v12,
v22)
смежны в графе G
тогда и
только тогда, когда или v11
=v12,
а v12
и v22
соседние
в G2,
или v12=
v22,
а v11
и v12
соседние в G1.
Рис 1.8
Очевидно,что
|G1G2|
= |G1|*|G2|,
а |U(G1G2)|
=|G1|*R2+|G2|*R1
Графы можно задавать тремя способами:
геометрически, аналитически и матрично.
Рис.
1.9 При
геометрическом представлении вершины
графа изображаются точками или
кружочками, а связи между вершинами –
линиями. Если задаётся орграф, то связи
называются дугами, если неограф –
рёбрами (рис. 1.9).
При
аналитическом задании граф задаётся
совокупностью множеств вершин и рёбер:
G=<V,
U>, гдеV={v1,
…vN},U={u1,…uR}
(вершины и рёбра пронумерованы). При
матричном способе представления граф
может быть задан матрицей смежности,
матрицей инцидентности или матрицей
весов.
При
этом матрица I(G)
обладает следующими свойствами:
Каждый
столбец матрицы I(G)
содержит только две единицы (граф без
петель). Для орграфа в матрице инцидентности
I(i,
j)=
1
в зависимости от направления дуги: “+1”
если вершина vi
является
началом дуги uj,
“-1”
если vj
– конец
uj.
Более компактным способом задания
графа по сравнению с матрицей Iявляется список концов рёбер, в котором
для каждого ребра задаётся пара
инцидентных ему вершин. В случае орграфа
в списке первой указывается начальная
вершина.
Рис.
1.10 Рис. 1.11
Для неографа матрица Sявляется симметричной, для ориентированного
– нет. В клетке матрицыS(i,
j)ставится 1,
если дуга имеет направлениеvi
vj
. В случае графа с кратными рёбрами
в соответствующей клетке матрицыSуказывается кратность соответствующего
ребра или его вес.
Например, для графа G1(рис. 1.10) матрица инцидентности имеет
вид: I(G1)
=
u1 u2 u3 u4 u5 u6 u7 v1 1 1 0 1 1 1 0 v2 1 1 1 0 0 0 0 v3 0 0 1 1 0 0 1 v4 0 0 0 0 1 1 1
Матрица смежности: S(G1)
=
v1 v2 v3 v4 v1 0 2 1 2 v2 2 0 1 0 v3 1 1 0 1 v4 2 0 1 0
Список концов ребер: u1 u2 u3 u4 u5 u6 u7 v1 v1 v2 v1 v1 v1 v3 v2 v2 v3 v3 v4 v4 v4
Для орграфа на рис. 1.11 матрица
инцидентности: I(G2)
=
u1 u2 U3 u4 U5 v1 1 0 -1 1 0 v2 -1 1 0 0 -1 v3 0 -1 1 0 0 v4 0 0 0 -1 1
Матрица смежности: S(G2)
=
v1 v2 V3 v4 v1 0 1 0 1 v2 0 0 1 0 v3 1 0 0 0 v4 0 1 0 0
Список концов ребер: u1 u2 u3 u4 u5 v1 v2 v3 v1 v4 v2 v3 v1 v1 v2
В прикладных задачах, решаемых с помощью
сетевых моделей, ребра графа часто
имеют одну или несколько характеристик
физического или экономического
характера: длина, пропускная способность,
стоимость и т. п. В этом случае граф
определяется одной или несколькими
матрицами размера NN.
В общем случае они называются матрицами
весов ребер, хотя могут иметь и специальные
названия (например, матрица стоимостей).
Важным понятием
в теории графов является связность. С
решением вопроса о связности в графах
связано решение ряда прикладных задач,
в частности, задача кодирования состояний
цифрового автомата. Рис
1.12 Рис.
1.13
Для
неографа и орграфа понятия связности
несколько отличаются.
Две вершины неографа считаются
связанными, если существует маршрут,
соединяющий эти вершины.
Граф
называется связным, если любые его две
вершины связаны. Очевидно, что в связном
графе между любыми двумя вершинами
существует цепь, так как из связывающего
их маршрута всегда можно удалить
участок, проходящий через некоторую
вершину более одного раза. Если граф
не связный, то множество его вершин
можно разделить на непересекающиеся
подмножества, каждое из которых содержит
все связанные между собой вершины и
вместе с инцидентными им ребрами
образуют связный подграф.
Компонентой
связности неографа G
называется его подграф G’,
удовлетворяющий следующим условиям: G’-
связный граф Добавление
в G’
любой вершины vi
из графа G
с рёбрами, инцидентными vi,
нарушает условие связности неографа
G’.
Связный
неограф всегда имеет только одну
компоненту связности. Ею является сам
неограф. Несвязный неограф состоит из
нескольких компонент связности. На
рис. 1.12 показан связный неограф, а на
рис 1.13 – несвязный, содержащий две
компоненты связности: G1
и G2.
Орграф
называется сильно связным, если для
любых его двух вершин vi
и vj
найдётся путь из vi
в vj
и путь из vj
в vi. Рис.
1.14 Рис. 1.15 Рис. 1.16
Орграф
называется несильно связным, если для
любых двух вершин vi
и vj
найдётся путь либо из vi
в vj,
либо из vj
в vi.
В остальных случаях граф называется
несвязным.
Граф
на рис. 1.14 - сильно связный, на рис. 1.15 –
несильно связный, а на рис. 1.16 – несвязный.
Компонентой
сильной связности орграфа G
называется его подграф G’,
удовлетворяющий следующим условиям: G’
– сильно связный граф; Добавление
в G’
любой вершины vi
из G
с дугами, инцидентными vi,
нарушает условие сильной связности
подграфа G’.
Сильно связный
орграф всегда имеет только одну
компоненту сильной связности, которой
является сам граф.
Если
граф G
= <V,
U>
имеет p
компонент связности: G1
= <V1,
U1>,
… , Gp
= <Vp,
Up>,
то очевидно, что
1)
V=V1
V2
….
Vp;
U= U1
U2
…..
Up;
то есть G=
G1
…
Gp;
2)
Vi
Vj
= ,
Ui
Uj
=
при
i
j;
3)
N1
+
N2
+
….+ Np=N;
R1
+ R2
+....+Rp=R.
Ребро,
при удалении которого граф превращается
в несвязный, называют мостом. На рис.
1.17 - R
– мост.
Рис 1.17
Вершина, при
удалении которой вместе с инцидентными
ей рёбрами, граф становится
несвязным, называется сочленением.
Граф,
не имеющий мостов и сочленений, называется
неразделимым.
Если
G’
получен из G
удалением некоторых вершин, то S(G’)
может быть получена из S(G)
вычеркиванием строк и столбцов,
соответствующих удаленным вершинам.
Рис
1.18 Рис
1.19
При проектировании сетей ЭВМ часто
возникает задача следующего вида:
имеется сеть, состоящая из центров
хранения и передачи информации. Некоторые
центры попарно соединены каналами,
обмен информацией между центрами
происходит либо непосредственно по
каналу, если он есть, либо через другие
центры и каналы.
Сеть
считается исправной, если каждая пара
центров может обмениваться информацией.
Такой сети, естественно, можно поставить
в соответствие граф, вершины которого
– центры, а рёбра – каналы. Исправной
сети будет соответствовать тогда
связный граф.
Важнейшим
понятием, относящимся к такой сети,
является её надёжность, под которой
подразумевается способность
функционировать при выходе из строя
нескольких каналов или центров. Очевидно,
что более надежной считается сеть,
исправность которой не нарушается при
выходе из строя меньшего числа элементов.
Надёжность сети можно оценить на
основании следующих определений.
Числом
вершинной связности графа ()
называется наименьшее число вершин,
удаление которых делает граф несвязным
или одновершинным. Рис
1.20
Например,
для полного графа 1-ого порядка (G1)=0,
(G
n)=N-1,
для простого цикла
(C
n)=2
(см. рис 1.20).
Числом
рёберной связности графа ()
называется минимальное число рёбер,
удаление которых превращает граф в
несвязный. Если граф одновершинный,
(G)=0.
(G)
(G)
Для
рассматриваемого примера сети ЭВМ
числа (G)
и (G)
отражают чувствительность сети к
разрушению центров и каналов, а точки
сочленения и мосты оказываются наиболее
уязвимыми местами сети.
Если
deg(G)
– минимальная степень вершин графа
G,
то очевидно, что (G)deg(G),
поскольку удаление всех рёбер, инцидентных
данной вершине, приводит к увеличению
числа компонент графа. Почти для всех
графов (G)=(G).
Если
граф G
несвязный или имеет мост, очевидно, что
(G)
=(G),
а для любого графа верно неравенство:
(G)
(G)
(G)
Граф
G
называется k-связным,
если (G)
k,
и ребёрно k-связным,
если (G)
k
(рис. 1.21,
1.22).
Таким образом,
граф односвязен тогда и только тогда,
когда он связен, а двусвязные графы (2
–связные) –это графы без точек соединения
и мостов.
Рис 1.21
(k4)=3
(k4)=3
Граф
3 –связен.
Рис 1.22
(
C4)=2
(
C4)=2
Граф
2 –связен На
рис 1.23 показан односвяз две компоненты–
1- связную На
рис 1.24 показан двухсвяз 2
компоненты - 3- связную и
Рис 1.23
ный граф,
содержащий и
2- связнную
ный граф,
содержащий 2-связную
Максимальный
k-связный
подграф называется k-компонентой
графа или k-связной
компонентой.
Особую
роль в теории графов играют случаи,
когда k=2
и k=3,
поскольку, во-первых, такие графы
встречаются в большинстве теоретических
и практических задач, во-вторых, при
таком числе связности удается дать
обозримое описание графа.
Свойства двусвязных
графов:
Степени вершин 2-связного графа больше
1. Если
G1
и G2
двусвязные и имеют не менее двух общих
вершин, то граф G1G2
тоже двусвязный (рис. 1.24). Если
G-двусвязный
граф, P-
цепь, соединяющая две его вершины, то
граф G
P
тоже двусвязный. Если
вершина v
не является точкой сочленения в связном
графе, то любые две его вершины соединены
цепью, не содержащей v
, в частности в двусвязном графе для
любых трёх несовпадающих вершин a,
b,
v
всегда имеется цепь (a,
b),
не проходящая через v.
В
1927 году К. Менгер доказал теорему,
устанавливающую связь между числом
непересекающихся простых цепей,
соединяющих две несмежные вершины
графа, и его связностью.
Теорема
Менгера: Наименьшее число вершин,
разделяющих две несмежные вершины
графа a
и b,
равно наибольшему числу попарно
непересекающихся простых (a,
b)-цепей
этого графа.
Из теоремы Менгера непосредственно
следует:
Граф
k-связен
тогда и только тогда, когда любая пара
его несовпадающих вершин соединена по
крайней мере k
непересекающимися цепями.
Два
графа G1=<V1,
U1>
и G2=<V2,
U2>
называются изоморфными, если существуют
взаимно –однозначные отображения :
V1
V2
и :
U1
U2
такие, что сохраняются отношения
инцидентности и ориентации, то есть,
если uk=(vi,vj),
в графе G1,то
(uk
)=(
(vi
),
(vj
))
в графе G2:
{vi,
vj
}
U1
{(
vi),
(vj)}
U2
Рис
1.25
На
рис. 1.25: графы G1
и G2
– изоморфны, а граф G3
– не изоморфен G1
и G2.
То есть два графа являются изоморфными,
если они совпадают с точностью до
нумерации вершин. По конфигурации
изоморфные графы могут существенно
отличаться, но у них сохраняются связи
между вершинами. Матрицы I
и S
задают графы с точность до изоморфизма.
Чтобы определить, задают ли матрицы
смежности изоморфные графы, можно
провести всевозможные перестановки
строк и столбцов. Если после какой-либо
перестановки матрицы S
окажутся тождественными, то соответствующие
графы изоморфны. Однако чтобы убедиться
таким способом в неизоморфности графов,
нужно сделать n!
перестановок, что весьма трудоёмко.
Изомофизм является
отношением эквивалентности на множестве
графов.
Планарные
графы широко используются при решении
таких задач, как прокладка различных
путей и сетей на плоскости, и при
проектировании микро-устройств для
определения количества слоёв печатных
плат.
Граф называется планарным, (или плоским)
если существует изоморфный ему граф
(в геометрическом представлении),
который может быть изображен на плоскости
без пересечения рёбер. Рёбра могут
пересекаться только в вершинах графа.
Например, графы на рис. 1.25 – планарные.
Два
графа называются гомеоморфными, если
они изоморфны с точностью до вершины
второй степени, то есть, если после
удаления из них вершин 2-ой степени и
объединения инцидентных им рёбер графы
оказываются изоморфными (на рис. 1.26
показаны гомеоморфные графы G1
и G2.
Рис 1.26
Введение
понятия гомеоморфности позволяет
сформулировать критерий планарности
графа. Рис.
1.27
На
рис. 1.27 изображены графы K5
и K3,3,
называемые графами Понтрягина. K5
- это
полный граф с пятью вершинами (пятого
порядка), двудольный граф K3,3
–
третьего
порядка, возникающий при решении
известной задачи о трех домах и трех
колодцах.
С
помощью методов математического анализа
можно доказать, что графы Понтрягина
планарными не являются. Понятно, что
тогда не является планарным и любой
граф, содержащий подграф, гомеоморфный
одному из графов Понтрягина.
Имеет
место следующая теорема, представляющая
критерий планарности графа.
Теорема
(Понтрягина – Куратовского). Граф
является планарным тогда и только
тогда, когда он не содержит подграфов,
гомеоморфных одному из графов Понтрягина.
Задачи, связанные с эйлеровыми, а,
особенно, с гамильтоновыми графами
часто встречаются и в головоломках, в
игровых задачах, на практике, в частности,
когда для выполнения некоторого
комплекса операций необходимо провести
их в таком порядке, чтобы эффективность
их выполнения была максимальной. К
этому же классу задач относится и
известная задач о кенигсберских мостах,
которая на языке теории графов
формулируется так: есть ли в мультиграфе
Gцикл, соединяющий все
рёбра мультиграфа?В 1736 году Эйлер
доказал, что эта задача неразрешима,
но при этом сформулировал важное
условие, при котором связный граф
содержит эйлеров цикл.
Цикл
называется эйлеровым, если он содержит
все рёбра графа, а связный граф с
эйлеровым циклом называется эйлеровым.
Эйлеров граф можно нарисовать, не
отрывая ручки от бумаги и не повторяя
линий.
Существует также
понятие эйлеровой цепи, то есть цепи,
содержащей все рёбра графа.
Эйлер в 1736 году
сформулировал теорему:
Теорема
Эйлера: Связный граф является эйлеровым
тогда и только тогда, когда степени
всех его вершин чётны. (Докозательство
тривиально)
Естествено,
возникает вопрос об отыскании в любом
графе эйлерова цикла, то есть о такой
нумерации рёбер G,
чтобы номер указывал, каким по счёту
это ребро входит в эйлеров цикл.
Один из алгоритмов
нумерации называется алгоритмом Флёри: Начиная
с произвольной вершины vi
присваивается произвольному ребру
(vi
vi+1)
номер 1, затем это ребро вычёркивается
и переходят в вершину vi+1. Пусть
vi
– это вершина, в которую пришли на
предыдущем шаге, а k-
это номер, присвоенный некоторому
ребру на этом шаге. Выбирается любое
ребро, инцидентное вершине vi,
причём, мост выбирается только в том
случае, когда нет других вариантов.
Ребро обозначается номером k+1
и вычёркивается. Действия
продолжаются до тех пор, пока не будут
вычеркнуты все рёбра графа, то есть
занумерованы. Рис
1.28 На
рис. 1.28 показана нумерация ребер,
выполненная по алгоритму Флёри. Следует
отметить, что эйлеровы графы на практике
достаточно редки.
Граф называется
гамильтоновым, если в нём имеется
простой цикл, соединяющий каждую вершину
графа. Сам цикл также называется
гамильтоновым. Гамильтоновой называется
и цепь, соединяющая все вершины графа.
В 1859 году известный ирландский математик
У. Гамильтон придумал задачу «Кругосветное
путешествие». Каждой вершине додекаэдра
приписывается название одного города.
Задача состоит в том, чтобы, переходя
по рёбрам от одной вершины к другой,
вернутся в исходную вершину. То есть
нужно отыскать в графе простой цикл,
содержащий все вершины (рис. 1.29). Рис 1.33
Рис
1.30 N=9; deg(v)
4,5– должно быть, но deg(v1)=2.
Не все графы гамильтоновы, хотя бы
потому, что гр аф, имеющий простой цикл,
должен быть двусвязным.
В отличие от эйлерова графа, для
гамильтонова графа не существует
простого алгоритма нахождения
гамильтонова цикла.
До сих пор эта задача представляет
большой интерес и до конца не решена.
Однако существует ряд теорем, которые
можно использовать на практике,
доказывающих наличие гамильтоновых
циклов в связных графах.
Теорема
Дирака: Если граф G-
связный граф, N
3 и deg(v)
N/2 для любой
из вершин v,
то граф G
– гамильтонов. На рис. 1.30 показан граф,
гамильтоновым не являющийся.
Наиболее сильная
теорема о гамильтоновых графах
(У.Татт,1946):
Всякий
4-связный планарный граф является
гамильтоновым.
Для
точного решения этой задачи можно
использовать прямой перебор.
Класс деревьев занимает в теории графов
особое положение. С одной стороны, эти
графы достаточно просто устроены, и
задачи, трудно решаемые в других
условиях, с помощью графов этого класса
решаются достаточно легко. С другой
стороны, деревья часто встречаются в
областях, не имеющих к теории графов
прямого отношения.
Деревья открывали независимо несколько
раз. Кирхгоф ещё в прошлом веке ввёл
деревья и применил к исследованию
электрических цепей. А.Кэли
использовал их в химии для описания
структуры органических соединений.
Тогда же деревья были введены и
исследованы К. Жорданом как чисто
математические объекты.
Деревом
называется простой связный граф, не
содержащий циклов. Две вершины такого
графа связаны только одной цепью.
Деревья определялись по-разному.
Некоторые
из определений приведены в следующей
теореме (они же являются свойствами
деревьев):
Теорема:
Для графа G
с N
вершинами и R
рёбрами следующие утверждения
эквивалентны: G-дерево; G-связный
граф, R=N-1; G-ациклический
граф, R=N-1; любые
две несовпадающие вершины графа G
соединяет единственная простая цепь; G-ациклический
граф, такой, что, если какую-либо пару
его несмежных вершин соединить ребром,
то граф будет содержать ровно один
цикл.
Примеры деревьев
приведены на рис. 1.31.
Рис 1.31 Рис
1.32
Рис. 1.33
Дерево,
имеющее N
вершин, всегда содержит R=N-1
ребро, то есть минимальное количество
рёбер для того, чтобы граф был связным.
Если из дерева удалить хотя бы одно
ребро, то граф становится несвязным,
он распадается на компоненты, которые
могут быть также деревьями или отдельными
вершинами. При добавлении в дерево
ребра образуется цикл.
Несвязный
граф, компонентами которого являются
деревья, называется лесом. На рис. 1.32
показано образование цикла (а) и
разложение дерева на компоненты (б).
Среди
различных деревьев особо выделяют
последовательное дерево, представляющее
простую цепь ( рис. 1.33а), и звёздное
дерево, в котором одна из вершин –
центр, смежная со всеми остальными
вершинами (рис. 1.33б).
Если
в каждой компоненте связности графа G
есть дерево H,
то H
называется остовом графа G.
Если
в связном графе G
последовательно удалять ребра, входящие
в какой-либо цикл (циклические ребра),
то в конце концов получится дерево,
содержащее все вершины исходного графа.
Такое дерево называется остовом графа
G.
Если граф несвязный, то его остовом
является лес, состоящий из деревьев,
являющихся остовами компонент связности
графа.
Число
рёбер произвольного графа G,
которые необходимо удалить для получения
остова, не зависит от последовательности
их удаления и равно (G)=R-N+K,
где K
–число компонент связности G.
Число
(G)=R-N+K
называется цикломатическим числом
графа G.
(G)
определяет меру связности графа.
Для
леса =0,
для связного дерева (H)=0,
так как R=N-1,
K=1
(=N-1-N+1).
Граф имеет единственный цикл тогда и
только тогда, когда (G)=1.
Любой граф, в котором число рёбер не
меньше, чем число вершин, содержит цикл.
Естественно возникает вопрос: как много
остовов в графе? Для полного графа
число остовов равно NN-2.
(N-число
вершин ).
Теорема
Кирхгофа (1847г.) Число остовов в связном
графе G
порядка N2
равно алгебраическому дополнению
любого элемента матрицы Кирхгофа B(G)
= I*IT. Рис.
1.34
В
приложениях часто бывает так, что одна
из вершин дерева, а также ее взаимосвязи
с остальными вершинами, имеют особое
значение. В этом случае
удобно
рассматривать корневые деревья. В
неориентированном случае в качестве
корня дерева может рассматриваться
любая вершина. Тогда соседние с ней
вершины называются
вершинами
первого уровня (яруса), соседние с ними
(отличные от корня) – вершинами второго
уровня и т. д. Корневое дерево удобно
изображать в виде укладки, располагая
вершины одного уровня на одной высоте
(рис. 1.34). Рис.
1.35
Если
в корневом дереве выбрать некоторую
вершину v,
то множество всех вершин, связанных с
корнем цепями, проходящими через v,
называется ветвью для v
в корневом дереве. Ветвь – это подграф
корневого дерева, который сам является
корневым деревом с корнем в v
(рис. 1.35).
В
случае ориентированного графа вводится
понятие ориентированного дерева. Если
все рёбра графа направлены в сторону
вершины более высокого уровня, то дерево
называется ориентированным. В каждую
вершину ориентированного дерева входит
только одно ребро (или ни одного, если
это кореень).
Если все рёбра
графа направлены к корню, то дерево
называется схемой сборки. Что
такое граф? Каковы его элементы? Какие
отношения существуют между элементами
графа? Какой
граф называется неографом? Какой
граф называется орграфом? Что
такое мультиграф? Какой
граф называют простым? Что
такое маршрут, цепь и цикл в неографе? Что
такое путь и контур в орграфе? Что
такое подграф? Какие
операции выполняются над графами? Какими
количественными характеристиками
описываются графы? Какие
существуют способы для задания
графов? Какие
графы называют изоморфными и
гомеоморфными? Как
определяется связность неографа и
орграфа? Что
такое к-связный граф? Что
такое компонента связности графа? Как
определить, является ли граф эйлеровым
или гамильтоновым? Что
такое планарный граф? Что
такое остав графа? Как
определяется число оставов в графах
различных видов?
Практический интерес при решении задач
на графах представляют алгоритмы,
позволяющие существенно повысить
эффективность решения этих задач.
Алгоритмы поиска в графе (или алгоритмы
обхода графа) представляют методы
обхода всех вершин и рёбер графа. Во
многих случаях они являются основой
разработки других быстрых алгоритмов
на графах.
Пусть
G
- неограф и притом связный. В процессе
поиска в глубину вершинам G
присваиваются номера, а рёбра помечаются.
Вначале рёбра не помечены, вершины не
имеют номеров. Произвольной вершине
присваивается номер P(v0)=1,
выбирается произвольное ребро (v0,v1)
и помечается как «прямое», а вершина
v1
получает
номер P(v1)=2.
После
этого переходим в вершину v1.
Пусть на каком-то шаге процесс привёл
в вершину vk
и P(vk)=k+1.
Далее возможны следующие варианты: Имеется
непомеченное ребро (vk,).
Если у вершины
уже есть номер, то ребро (vk,)
помечается как «обратное» и продолжается
поиск неотмеченного ребра, инцидентного
vk.
Если же вершина
не имеет номера, то P()=k+2,
ребро (vk,)
помечается как «прямое» и переходят
в вершину . Все
рёбра, инцидентные вершине vk,
помечены. В этом случае идёт возврат
в вершину, из которой vk
получила свой номер.
Процесс
заканчивается, когда все рёбра будут
помечены и произойдет возврат в v0.
Рассмотрим
один из алгоритмов, обеспечивающих
указанную трудоёмкость.
Граф
задаётся списками смежности, то есть
Nv
– список вершин, смежных v.
Вершина, получившая номер P,
включается в список
и исключается из него сразу, как только
произойдёт возвращение из этой вершины.
Результат работы алгоритма – четыре
списка: P,
F,
T
и B.
P(v)-P-номер
вершины v;
F(v)
– имя вершины, из которой вершина v
получила свой номер; T
и B
– соответственно, списки «прямых» и
«обратных» рёбер графа G.
Эти рёбра получают ориентацию в
результате работы алгоритма А1:
если ребро XY
помечается из вершины X
как «прямое», то в Т
заносится дуга (X,Y);
если как «обратное», его дуга (X,Y)
заносится в В. Алгоритм
поиска в глубину в неориентированном
связном графе:
Шаг 1. P(v0):=1;
(1):=v0;
Т:=;
В:=;
F(v0):=;
k:=1; p:=1,(k-
последний присвоенныйP-номер,p-указатель конца списка,
т.е.(р)-
имя последней вершины из);
Шаг 2. v:= (р)(р-исследуемая вершина);
Шаг 3. Просматривая список Nv,
найти такую вершину,
что реброvне помечено и перейти к шагу 4. Если
таких вершин нет, то перейти к шагу 5.
Шаг 4. Если вершина имеетР-номер, то пометить реброvкак «обратное» и занести дугу(v,)в списокВ. Перейти к шагу 3 и
продолжить просмотр спискаNv.
Иначеk:=k+1,Р()=k,
F():=v,реброvпометить как «прямое» и дугу(v,)занести в списокТ; р:=р+1, (р):=(вершинаполучилаР-номер и занесена в).
Перейти к шагу 2.
Шаг 5. р:=р+1(вершинаvвычеркнута из).
Еслир=0, то конец. Иначе перейти к
шагу 2
Пример:
задан граф G
и списки смежности (рис. 2.1), результат
работы алгоритма приведен на рис 2.2. Рис
2.1 Рис
2.2 N1=(3,2,5),
N2=(1,5,4),
N3=(1,5),
N4=(2,5),
N5=(1,2,3,4,6,7),
N6=(5,7), N7=(5,6)._________ P()=(1,2,3,4,5,6,7). P(1)=1;
Q(1)=1;
T=;
B;
F(1)=.
N7=(5,6)._________
P()=(1,2,3,4,5,6,7).
1)
P(1)=1;
Q(1)=1;
T=;
B;
F(1)=. P(3)=2;
Q(2)=3;
F(3)=1;
T=(1,3). P(5)=3;
Q(3)=5;
F(5)=3;
T=(1,3),(3,5). B=(5,1). P(2)=4;
Q(4)=2;
F(2)=5;
T=(1,3),(3,5),(5,2). P(4)=5;
Q(5)=4;
F(4)=2;
T=(1,3),(3,5),(5,2),(2,4). B=(5,1),(4,5). B=(5,1),(4,5),(2,1).
Одна
из задач, решаемых с помощью этого
алгоритма – выделение связных компонент
графа. Для этого просматривается список
вершин G
и выполняются действия: если вершина
vi
имеет номер, то перейти к следующей.
Иначе положить v0=v1,
P(v0)=k+1,
где k-последний
присвоенный номер и т.д. После окончания
поиска (т.е., выделения компоненты,
содержащей vi)
продолжить просмотр списка, перейти к
вершине vi+1.
Различать вершины разных компонент
можно, например, по их номерам, если для
каждой компоненты запомнить номер P.
Таким
образом, дуги множества Т
образуют
ориентированный
остов с корнем в вершине v0.
Задача раскраски вершин или рёбер графа
занимает особое место в теории графов.
Характерной особенностью этих задач
является существование объектов,
которые по какой-либо причине не могут
быть объединены в одну группу.
Если
G=<V,U>
– некоторый граф, а k
– натуральное число, то произвольная
функция f:
V{1,2,…,k}
называется вершинной k-раскраской
или просто k-раскраской
графа G.
Раскраска называется
правильной, если V{1,2,…,k}, f
(v)f
(u) для
любых соседних вершин v
и u.
Граф,
для которого существует правильная
k-раскраска,
называется k-раскрашиваемым
(или раскрашиваемый k
цветами). Правильную k-раскраску
можно интерпретировать как окрашивание
каждой
вершины G
в один из k
цветов, при этом смежные вершины должны
получить различные цвета. При k-
раскраске может быть использовано
меньше k
цветов и правильную раскраску можно
рассматривать как разбиение V
=V1
V2
…V
l,
где l
k
Множества
вершин V
графа G,
на не более чем k-непустых
классов, каждый из которых является
независимым множеством. Классы V1,V2,…
называются цветными классами. Минимальное
число k,
при котором граф G
имеет правильную раскраску, называется
хроматическим числом этого графа и
обозначается (G).
Если (G)=k,
то граф
называется k-хроматическим
и его раскраска является
минимальной. Рис.
2.3. Пример правильной раскраскиграфа.
Пример
правильной раскраски приведен на рис.
2.3. Меньшим числом цветов этот граф
раскрасить нельзя, так как имеется
цикл, для правильной раскраски которого
требуется не менее 2-х цветов, и ещё один
цвет – для вершины 3 (=3).
Примеры
задач, сводящихся к правильной раскраске: Задача
составления расписаний. Предположим,
что нужно прочесть несколько лекций
в кратчайший срок. Чтение каждой лекции
в отдельности занимает один час, но
некоторые лекции не могут читаться
одновременно (один и тот же лектор).
Строится граф G,
вершины которого соответствуют лекциям,
и две вершины смежны тогда и только
тогда, когда соответствующие лекции
нельзя читать одновременно. Очевидно,
что любая правильная раскраска этого
графа определяет допустимое расписание:
лекции, соответствующие вершинам
графа, составляющим один цветной класс,
читаются одновременно. И, наоборот,
любое правильное расписание определяет
правильную раскраску графа G.
Оптимальные расписания соответствуют
минимальным раскраскам, и число часов,
необходимое для прочтения всех лекции,
равно (G).
Задача
распределения оборудования. Заданы
множества V={v,…vN}
и S={s1,…,sm}
работ и механизмов соответственно.
Для выполнения каждой из работ требуется
некоторое время, одинаковое для всех
работ, и некоторые механизмы. При этом
никакой из механизмов не может быть
занят одновременно на 2-х или более
работах. Нужно распределить механизмы
так, чтобы общее время выполнения всех
работ было минимальным. Строится граф
G,
в котором vi
и vj
(ij)
смежны тогда и только тогда, когда для
выполнения работ vi
и vj
требуется
хотя бы один общий механизм. При
правильной раскраске графа G
работы, соответствующие вершинам
одного цвета, можно выполнить
одновременно, а наименьшее время
выполнения всех работ достигается при
минимальной раскраске.
Для
некоторых графов несложно найти
хроматические числа: (KM)=M;
(KM-r)=M-1;
(KN,M)=2;
(C2M)=2;
(C2M+1)=3.
Очевидно, что граф 1- хроматический,
когда он пустой. 2- хроматический –
когда он двудольный и непустой.
Задачи
определения хроматического числа и
построения минимальной раскраски
произвольного графа являются очень
сложными, эффективные алгоритмы их
решения неизвестны, однако существуют
алгоритмы построения правильной
раскраски, в ряде случаев приводящие
к минимальной раскраске. Алгоритм
последовательной раскраски:
Шаг 1. Произвольной вершине v1графаGприсваивается
цвет1.
Шаг 2. Если вершины v1,
v2,…vi
раскрашеныLцветами1,2,…L,
L
i, то новой произвольно
взятой вершинеvi+1приписывается цвет, не использованный
при раскраске вершин из её окружения.
Поскольку
точная раскраска граф невозможна, имеет
смысл привести некоторые оценки
хроматического числа.
Для
любого графа G
верно неравенство: (G)
1+ max (H),
H
, где -
минимальная из степеней вершин графа
G;
-
множество всех порождённых подграфов
графа G.
Для
любого графа G
верно неравенство: (G)
1+G где
– максимальная из степеней вершин
графа G.
Рис
2.4
Если
G
– связный граф, не являющийся полным,
и G3,
то (G)
G.
Эта
оценка может быть завышенной, например,
(K1,
n)
n,
в то время как для двудольного графа
(K1,
n)=2,
(рис. 2.4.).
Одной
из самых знаменитых задач о раскрасках
является раскраска планарных графов.
Первоначально
вопрос формулировался так: достаточно
ли четырёх красок для такой раскраски
произвольной географической карты,
при которой две любые соседние страны
окрашены в различные цвета? При этом
рассматриваются лишь такие карты, в
которых граница любой страны состоит
из одной замкнутой линии, а соседними
считаются страны, имеющие общую границу
ненулевой длины.
Позже
задача была формализована: картой стали
называть связный плоский мультиграф
без мостов. Грани карты, имеющие общее
ребро, называются смежными. Функция О,
ставящая в соответствие каждой грани
натуральное число О:Г{1,2,…k}
–цвет грани Г
– называется k-раскраской,
если цвета смежных граней различны.
В
1879 году британский математик А. Кэли
сформулировал гипотезу четырёх красок
(задача была известна и ранее):
Всякая
карта 4-раскрашиваема (другими словами,
для раскраски планарного графа достаточно
точно четырёх красок).
По
аналогии с вершинной раскраской
существует
рёберная.
Очень
часто при решении прикладных задач
возникает проблема построения кратчайшего
связывающего или остовного дерева для
данного взвешенного графа, то есть
графа, ребрам которого приписаны
некоторые весовые коэффициенты.
Эта
задача возникает при проектировании
линий электропередач, трубопроводов,
дорог и т.п., когда требуется данные
центры соединить каналами связи так,
чтобы два центра были связаны либо
непосредственно каналом, либо через
другие центры и каналы и чтобы длина
каналов связи была минимальна. Центры
в этой задаче – это вершины, а каналы
связи – это рёбра с заданными длинами
(или весами). Тогда искомая сеть будет
кратчайшим остовным подграфом, который
является деревом. Вообще, деревья
используются в прикладных задачах,
решение которых заключается в установлении
связей между объектами кратчайшим
образом. Кроме того, деревья применяются
в задачах трассировки печатных плат,
при моделировании иерархических
структур.
Примеры:
1.
Несколько городов связаны между собой
сетью автомобильных дорог, качество
которых не является идеальным. Для
перевозки ценных грузов необходимо
для каждой пары городов наличие по
крайней мере одной хорошей дороги между
ними. Стоимость ремонта покрытия одного
километра каждой дороги известна.
Покрытие каких дорог требуется усилить,
чтобы затраты на ремонт всех дорог были
минимальны?
2.
Несколько населенных пунктов требуется
связать друг с другом сетью телефонных
линий. Известна стоимость прокладки
линии между двумя любыми пунктами. Где
следует проложить линии, чтобы затраты
были минимальными?
3.
Информационно-вычислительная сеть
связывает между собой вычислительные
центры нескольких предприятий. Ввиду
большого объема потока информации и
ограниченной надежности некоторые
линии сети могут оказаться блокированными.
Для проведения телеконференций
необходимо, чтобы каждые два предприятия
могли связаться друг с другом. Как в
произвольный момент времени определить,
возможна ли организация такой связи?
В
первом случае возникает задача поиска
кратчайшего остовного дерева данного
графа, во втором – кратчайшего
связывающего дерева для данных вершин
(оно же – остовное дерево полного
графа). В третьем случае требуется
определить, является ли данный граф
связным. Это может быть сделано, в
частности, с помощью построения любого
остовного дерева (не обязательно
кратчайшего).
Поскольку
полный граф GN
имеет число остовов NN-2,
то решение задачи путём перебора всех
вариантов требует больших вычислений.
Однако, для произвольного связного
графа существует несколько алгоритмов,
позволяющих эффективно решить данную
задачу.
Пусть
G=<
V,
U
> –
неориентированный граф с N
вершинами, {aij}
– матрица весов ребер, которые в данном
случае будем называть длинами ребер,
aij=,
если ребра между вершинами i
и j
нет, aii=0.
Следует отметить, что во многих случаях
понятие длины ребра является чисто
условным: числа {aij}
могут, вообще говоря, быть отрицательными
и не подчиняться неравенству треугольника.
Основная идея рассматриваемого ниже
алгоритма построения кратчайшего
связывающего (покрывающего) дерева
состоит в следующем. Просматриваются
ребра графа в порядке возрастания их
длин и для каждого ребра принимается
решение, будет ли оно включено в
строящееся дерево. Если ребро образует
контур с ранее включенными ребрами, то
оно не может входить в дерево, в противном
случае оно включается в дерево. Таким
образом, множество включенных ребер
образует лес, их количество возрастает.
Процесс заканчивается, если количество
включенных ребер становится равным
N-1
– это означает, что они образуют
покрывающее дерево, или если все ребра
исходного графа G
просмотрены, а покрывающее дерево все
еще не построено. В этом случае исходный
граф является несвязным, покрывающего
дерева не существует, а получившийся
лес является кратчайшим остовом
исходного графа.
Алгоритм Краскала
(построения кратчайшего остовного
дерева).
Обозначим
M
– множество ребер исходного графа G,
D1,
D2,
… - деревья,
которые будут образовывать включенные
ребра, n
– счетчик количества включенных ребер.
Перед началом выполнения алгоритма M
включает все ребра исходного графа G,
все Di
– пустые, n=0.
Шаг 1. Если множество Mпусто, то СТОП: остовного дерева не
существует, непустыеDiобразуют остов исходного графа (лес).
Шаг 2. Выбрать в множестве Mребро минимальной длины и исключить
его изM. Для этого
ребра возможны следующие случаи: Обе
инцидентные вершины не принадлежат
никаким деревьям Di.
Образовать из них и этого ребра новое
деревоDi,
n:=n+1. Одна
из вершин (концов ребра) принадлежит
дереву Di,
другая не принадлежит ни одному дереву.
Включить в деревоDiребро другую вершину,n:=n+1. Одна
из инцидентных вершин принадлежит
дереву Di,
другая – деревуDj.
Объединить оба дерева в одно, присоединив
ребро к новому дереву,n:=n+1. Обе
вершины принадлежат одному дереву Di.
В этом случае ребро не включается в
строящийся остов.
Шаг 3. Если n=N-1,
то СТОП: единственное непустое деревоDi– кратчайшее покрывающее дерево
исходного графа, иначе перейти к шагу
1.
Рис. 2.6
На рис. 2.6 приведен
граф и кратчайшее остовное дерево,
найденное с помощью алгоритма Краскала.
Двойной линией отмечены ребра,
просмотренные, но не включенные в дерево
в процессе работы алгоритма.
В таблице приведены
промежуточные результаты работы
алгоритма. Итерация Ребро Результат 2 шага n 1 (1,2) Образовано D1={1,2} 1 2 (1,3) Включено в D1,
D1={1,2,3} 2 3 (2,3) Не включено 2 4 (5,6) Образовано D2={5,6} 3 5 (3,5) D1,
D2 и
ребро(3,5)объединены в новое
дерево,D1={1,2,3,5,6}. 4 6 (2,5) Не включено 4 7 (3,6) Не включено 4 8 (3,4) Включено в D1,
D1={1,2,3,4,5,6}. 5
Имеются
и другие способы построения кратчайшего
остовного дерева, например, алгоритм
Прима, более простой для описания (но
не для реализации). В нем на каждом шаге
строится не просто ациклический
граф, а
дерево.
Шаг 1. Выбрать в графе ребро минимальной
длины и построить дерево D1,
состоящее из этого ребра и инцидентных
ему вершин.
Шаг 2. Если дерево Diпорядкаiуже построено
иi<N-1,
то среди рёбер, соединяющих вершины
этого дерева с вершинами графаG,
не входящими вDiвыбрать ребро минимальной длины.
Построить деревоDi+1,
присоединяя кDiэто ребро вместе с его не входящим вDi
концом, увеличитьiна единицу и перейти к шагу 2.
Если
этот алгоритм применить к графу из
рассмотренного примера, то ребра будут
включаться в дерево в следующем порядке:
(1,2), (1,3),
(3,5), (5,6), (3,4).
При решении практических задач с помощью
сетевого моделирования часто возникает
задача поиска пути, наилучшего по тому
или иному критерию, между двумя вершинами
графа.
Примеры задач:
1. Несколько городов, в том числе AиB, связаны между собой
сетью автомобильных дорог. Путешественник
отправляется из городаAв городB. Какой маршрут
он должен выбрать, чтобы добраться доB, проехав минимальное
расстояние?
2. В условиях предыдущей задачи
путешественник учитывает, что дороги
между городами имеют различное покрытие,
и, следовательно, для проезда по ним
расход горючего и затраты на него
являются различными. Поэтому он желает
проехать в город Bс
минимальными денежными затратами.
3. Предприятие, расположенное в городе
A, заинтересовано в
поставках габаритных грузов одному из
предприятий в городеB.
Однако на некоторых дорогах между
городами имеется ограничение на тоннаж
провозимого груза. Требуется определить,
какой максимальный груз может быть
провезен изAвB?
4. Несколько городов связаны между собой
сетью коммуникационных линий связи.
Каждая линия имеет ограниченную
надежность, и для нее известна вероятность
обеспечения нормальной связи. Фирма,
расположенная в городе A,
желает обеспечить с филиалом, расположенным
в городеB, связь по
наиболее надежному маршруту. Как его
найти?
Во всех приведенных примерах требуется
найти в графе путь между двумя узлами,
оптимальный по определенному критерию.
В первом случае это сумма длин ребер
пути, во втором – сумма затрат, т.е.
стоимостей проезда по данному ребру.
В третьем случае требуется найти путь,
для которого минимальное из ограничений
на вес груза является максимальным, а
в четвертом – путь, для которого
вероятность находиться в исправном
состоянии, то есть приизведение
соотретствующих вероятностей отдельных
ребер, принимает максимальное значение.
Таким образом, критерии оптимальности
требуемого маршрута могут быть
качественно различными. В первую очередь
мы рассмотрим проблему поиска пути,
минимального по длине (стоимости,
времени), которая представляет собой
суммарную длину (стоимость, время)
ребер, входящих в данный путь.
Предположим, что каждой дуге (i,j)ориентированного графа (случаи
неориентированного или смешаного графа
качественно ничем не отличаются, как
будет видно из дальнейшего) поставлено
в соответствие числоaij– длина дуги. (напомним, что понятие
«длины» здесь условное,aij- просто какие-то действительные числа).
Каждой паре узлов(i,j),для которых не существует дуги,
соединяющих их, приписывается длинаaij=.Задача
состоит в нахождении в данном графе
такого пути из узлаsв узелt, для которого
суммарная длина дуг минимальна.
Рассматриваемый здесь алгоритм
предназначен для поиска кратчайших
путей из заданного узла sв каждый из остальных узлов в случаеaij0и основан на так называемом «методе
пометок». Каждый узел графаiимеет меткуd(i),
которая на каждой итерации алгоритма
представляет собой длину кратчайшего
найденного пути в узелi.
Поэтому перед началом работы алгоритмаd(s)=0,
d(i)=
приis.
Еще одна меткаl(i)вводится для того, чтобы по окончании
работы алгоритма было возможно вычислить
последовательность вершин, образующих
каждый из кратчайших путей.
Пусть d(i)
- метка узла,S– множество
вершин.
Шаг 1. Положить d(s)=0,
d(i)=
приis,l(i)=0,S=
Шаг 2. Если в Sвходят все
вершины графа, то СТОП: длины кратчайших
путей найдены.
Шаг 3. Если для всех iSd(i)=
,то СТОП: не существует путей в
вершины, не входящие вS.
Иначе среди вершинiSнайти вершинуnс
минимальной меткой.
Шаг 4. Включить вершину nв множествоS, для всехkSвычислитьd(k)=min{d(k),d(n)+ank}.
Если при этом значениеd(k)изменяется, тоl(k)
положить равнымn.
Перейти к шагу 2.
Пример 1. В этом
алгоритме последовательно просматриваются
все вершины графа, причем каждый раз
выбирается вершина с минимальной меткой
из еще не просмотренных (при первой
итерации будет выбрана вершина s),
и затем для соседних с ней вершин
вычисляются новые значения меток как
минимальные из двух чисел: прежняя
метка и длина вновь найденного пути
через рассматриваемую вершину. Легко
видеть, что в случае aij0
минимальная метка для непросмотренных
вершин уже не может быть уменьшена в
дальнейшем и является длиной кратчайшего
пути в эту вершину. После выполнения
алгоритма с помощью метокl(i)
могут быть найдены кратчайшие пути.
Так, для пути изsвtпоследней будет вершинаt,
предпоследней –l(t),перед ней –l(l(t)),
и так далее, доs. Все
такие пути образуют дерево кратчайших
путей из вершиныs.
Рис. 2.7
Пример 2. Задача о покупке автомобиля.
При решении вопроса о том, через какое
время следует производить покупку
нового автомобиля, необходимо учитывать
его стоимость и возрастающие
эксплуатационные расходы. Рассматривается
восьмилетний период времени.
Предполагается, что решение о покупке
нового автомобиля может приниматься
в начале каждого года, исходя из затрат
на его приобретение, эксплуатационных
расходов на период, в течение которого
автомобиль будет использоваться, и
ликвидационной стоимостимашины в
момент, когда она заменяется на новую.
Предположим, что в начальный момент
человек не имеет автомобиля, и что он
собирается покупать новый автомобиль
по крайней мере каждые 4 года.
Сеть для рассматриваемой задачи содержит
9 вершин (рис.2.7). Если в начале i-го
года производится покупка автомобиля,
а в началеj-го года
автомобиль заменяется на новый, то
данному варианту замены соответствует
дуга(i,j).
Итерация Вершина 1 2 3 4 5 6 7 8 9 0 0 1 0 1450 2750 3850 4750 2 0 1450 2750 3850 4750 6900 3 0 1450 2750 3850 4750 6900 8550 4 0 1450 2750 3850 4750 6900 8550 10000 5 0 1450 2750 3850 4750 6825 8550 10000 11250 6 0 1450 2750 3850 4750 6825 8550 10000 11250 7 0 1450 2750 3850 4750 6825 8550 10000 11250 8 0 1450 2750 3850 4750 6825 8550 10000 11250 9 0 1450 2750 3850 4750 6825 8550 10000 11250
Для минимизации общих затрат покупку
автомобиля следует производить в начале
первого, пятого и девятого годов. Затраты
при этом составляют 11250$.
Алгоритм Дийкстры может находить
кратчайшие пути только в случае, если
длины ребер aijнеотрицательны, в противном случае
метки просмотренных вершин, т.е.
включенных в множествоS,
не обязательно являются длинами
кратчайших путей, и алгоритм не всегда
находит правильное решение.
Рис. 2.8
Например, при поиске путей из вершины
1 для графа, изображенного на рис 2.8,
вершина 1 получит метку 0, вершины 2 и 3
– метки 2 и 1. Далее минимальной будет
метка вершины 3, и вершина 4 получит
метку 2, которая в дальнейшем не изменится,
поскольку вершина 3 уже просмотрена.
Между тем кратчайший путь в 4 проходит
через вершины 1,2,3,4 и имеет длину 1. Более
того, при наличии ребер отрицательной
длины в графе может присутствовать
контур отрицательной длины, и тогда
кратчайших путей вообще не существует,
поскольку длину пути всегда можно
уменьшить, добавляя к нему несколько
обходов этого контура.
Рис.
2.9
Алгоритм Форда представляет собой
простую модификацию алгоритма Дийкстры
для случая, когда длины ребер могут
быть отрицательными. На шаге 4 алгоритма
следует проводить вычисление новых
меток не для kS,
а для всех соседних сnвершин. Если при этом изменяется метка
у вершины, уже входящей в множествоS,
то ее следует снова исключить изS.
Таким образом, одна вершина может быть
просмотрена несколько раз. Если в графеNвершин, то простой
путь не может содержать более чемNвершин. Следовательно, если при раборе
алгоритма Форда какая-либо вершина
просматривается более чемNраз, это значит, что в графе имеется
контур отрицательной длины.
Пример 3. Для графа на рис. 2.9 вычисление
длин кратчайших путей из вершины 1 с
помощью алгоритма Форда дает следующие
результаты. Выделены метки вершин,
входящих в S.
Итерация Вершина 1 2 3 4 5 6 7 8
9
0 0
1 0 4 4 5
2 0 4 7 4 5
3 0 3 7 4 6 5
4 0 3 6 4 6 5
5 0 3 6 3 6 5
6 0 2 6 3 5 5
7 0 2 5 3 5 5
8 0 2 5 3 5 5 9 0 2 5 3 5 5 10 0 2 5 3 5 5 11 0 2 5 3 5 5 12 0 2 5 3 5 5 13 0 2 5 3 4 5 14 0 2 5 3 4 5 15 0 2 5 3 4 5 16 0 2 5 3 4 5
При выполнении алгоритма некоторые
вершины просматриваются несколько
раз. Дерево кратчайших путей представлено
на рис. 2.9.
Алгоритмы Дийкстры и Форда предназначены
для поиска длин кратчайших путей из
данной вершины sв
остальные вершины графа. При решении
прикладных задач часто бывает необходимо
найти длины кратчайших путей из каждой
вершины графа в каждую из остальных.
Задача может быть решенаN-кратным
применением алгоритма Форда, однако
более прост и эффективен алгоритм
Флойда, специально предназначенный
для этой цели. ОбозначимD0={dij0}
матрицу длин ребер данного графа, причемdii0=0,dij0=,
если ребра(i,j)в графе нет,dij0=aijв остальных случаях. МатрицуD0
можно считать матрицей длин
кратчайших путей, проходящих через 0
промежуточных вершин. Далее в алгоритме
Флойда последовательно вычисляются
матрицы D1,…,
DN,
где матрицаDk
является матрицей длин кратчайших
путей, проходящих через вершины1,…,k.
Пусть матрицаDk-1={dijk-1}
известна. Кратчайший путь изiвj, проходящий через
вершины1,…,k, либо
проходит через вершинуk,
либо нет. Во втором случае его длинаdijk
равнаdijk-1, а в первом он является объединением
кратчайших путей через1…k-1изiвkи изkвj,
поэтому
dijk=min{
dijk-1,
dikk-1+dkjk-1}.
Теперь можно описать алгоритм Флойда
Шаг 1. Построить матрицу D0,
Шаг 2. Для k=1,…,Nвычислить матрицыD1,…,
DNпо правилуdijk=min{
dijk-1,
dikk-1+dkjk-1}.
Рис 2.10
Пример 4. Для графа на рис. 2.10 вычисление
длин кратчайших путей по алгоритму
Флойда приводит к следующим результатам:
Матрица D6является матрицей длин кратчайших
путей данного графа. Наличие в ней
элементов, равных бесконечности,
означает, что для данных пар узлов ни
одного пути в графе не имеется. Сами
пути могут быть найдены по матрицамD0иD6с помощью
«обратного просмотра». Например, для
пути из 1 в 6 последней вершиной является
6, а предпоследней должна быть вершинаkтакая, чтоd1,66=d1,k6+dk,60.
Легко видеть, что это вершина 4. Далее
аналогично можно найти вершину,
предшествующую 4, и так далее, до вершины
1. В итоге получается путь {1,3,5,4,6}.
В предыдущем разделе рассматривалась
проблема поиска одного оптимального
пути для одной или нескольких пар вершин
в графе. Между тем на практике часто
возникает ситуация, когда определенное
количество единиц того или иного
продукта может передаваться из одного
пункта в другой по различным путям.
Примеры:
1. В период ведения военных действий
для материального обеспечения войск
требуется провести конвой, включающий
12 транспортных единиц, от военной базы
до места сосредоточения войск. Система
дорог, связывающая эти два пункта, может
быть представлена графом, в котором
дуги соответствуют участкам дорог, а
вершины – точкам пересечения этих
дорог. Из соображений безопасности для
каждого участка дорог установлено
ограничение на количество транспортных
единиц, которые можно по нему провести,
а также известна ожидаемая величина
потерь. Требуется определить маршрут
следования каждой транспортной единицы
так, чтоба обеспечить максимальную
безопасность конвоя.
2. С нескольких скважин нефть перекачивается
по системе трубопроводов на
нефтеочистительный завод. Пропускная
способность каждого трубопровода
известна. Требуется определить количество
нефти, которое должно перекачиваться
по каждому трубопроводу, так чтобы
максимизировать количество нефти,
доставляемое на завод.
3. При передаче цифровых сообщений по
каналам информационно-вычислительной
сети часто используется режим коммутации
пакетов, когда сообщение делится на
пакеты определенной длины, которые
могут передаваться по различным
маршрутам независимо друг от друга.
Время передачи пакета по каждому каналу
известно. Необходимо определить путь
передачи для каждого пакета, чтобы
время передачи всего сообщения было
минимальным.
4. В предыдущем примере известна стоимость
передачи пакета для каждого канала
сети. Требуется минимизировать стоимость
передачи сообщения.
В каждом из приведенных примеров
какой-либо объект (конвой, нефть,
сообщение) может передаваться с
начального пункта (источника) на
конечный (сток) не по одному пути,
а отдельными частями (транспортные
единицы, баррели (галлоны, литры), пакеты)
по различным путям. При этом имеются
ограничения на количество единиц
объекта, которые могут передаваться
по отдельным линиям сети. Все это
является характерной особенностью
потоковых задач, которые будут
рассматриваться в данном разделе. В
общем случае поток в сети – это способ
пересылки некоторых объектов из одного
пункта в другой. В конкретных случаях
это может быть транспортировка готовой
продукции, перемещение больших масс
людей и т.п. Однако имеется также большое
количество прикладных задач иного
характера, которые также могут быть
решены с помощью потоковых моделей.
Введем определение потока в сети. Пусть
имеется ориентированный граф, содержащий
Nвершин иRдуг, в котором заданы две вершины -
источникsи стокt,
а для каждой дуги – неотрицательное
числоCij,
называемоепропускной способностьюдуги(i,j).ПотокомизsвtвеличиныVназывается набор чисел {fij},i,j=1,…,N,
такой, что выполнены следующие условия:
При этом fij- величина потока на дуге(i,j).
Условие (2.5.1) представляет собой принцип
сохранения потока: из источникаsисходит поток величины V,
такой же поток входит в стокt,
а в промежуточных вершинах поток не
может ни возникать, ни исчезать:
количество потока, входящего в вершину,
равно количеству потока, выходящего
из нее. Условие (2.2) предусматривает,
что величина потока на каждой дуге не
должна превышать пропускную способность
дуги, подобное условие характерно для
многих прикладных задач.
Главная задача, которая возникает в
всязи с понятием потока в сети – это
задача о поиске максимального потокаизsвt.
Требуется найти набор чисел {fij}
, удовлетворяющий условиям (2.1) и (2.2),
при котором величина потокаVмаксимальна. Постановка задачи может
быть записана следующим образом:
Понятно, что если пропускная способность
дуг сети конечна, то максимальный поток
в ней также будет конечным. Например,
очевидно, что величина потока не может
быть больше суммы пропускных способностей
дуг, исходящих из источника s.
Введем несколько определений, которые
в дальнейшем будут непосредственно
связаны с понятием потока в сети.
Пусть X– некоторое
множество вершин графа такое, чтоsX,
аtX.
Множество дуг(i,j)таких, что один конец дуги принадлежитX, а другой не принадлежитX, называетсяразрезом.
Разрез, таким образом, - это множество
дуг, исключение которых из сети отделило
бы некоторое множество узлов от остальной
части узлов. Дуги(i,j)такие, чтоiX,
аjX,
называютсяпрямымидугами разреза.
Если жеjX,iX,
то дуга называетсяобратной.Пропускной способностью разрезаназывается величина, равная сумме
пропускных способностей всех прямых
дуг разреза. Разрез называетсяминимальным, если его пропускная
способность является наименьшей среди
всех разрезов сети. Понятно, что в сети
может быть несколько минимальных
разрезов. Разрез называетсянасыщенным,
если для прямых дуг величина потока
равна пропускной способностиfij=Cij,
а для обратных дугfij=0.
Интуитивно ясно и легко доказуемо, что
максимальная величина потока в сети
не может превосходить пропускную
способность любого разреза, в том числе
минимального. Имеет место и более
сильный результат.
Теорема о максимальном потоке и
минимальном разрезе(Форд, Фалкерсон).
Величина максимального потока в сети
равна пропускной способности минимального
разреза.
Доказательство фактически будет
содержаться в построении алгоритма
поиска максимального потока,
рассматриваемого далее. Там же будет
видно, что если поток в сети максимальный,
то в ней есть насыщенный разрез,
являющийся минимальным.
Рис. 2.11
Пример. В графе на рис 2.11 числа на дугах
обозначают пропускную способность и
величину потока (числа в скобках). Поток
V=6является
максимальным, насыщенный разрез
обозначен пунктирной линией.
Другая важная задача, которая часто
возникает при применении потоковых
моделей, - это задача о поиске потока
минимальной стоимости. Пусть кроме
пропускных способностейCij,
для каждой дуги задана стоимостьaijпередачи единицы потока по этой дуге.
Требуется найти поток в сети заданной
величиныV, имеющий
минимальную стоимость.
С этой задачей тесно связана еще одна:
о поиске максимального потока
минимальной стоимости.
Необходимость решения этих задач очень
часто возникает на практике, особенно
при рассмотрении экономических моделей.
К этому типу относится приведенный
ранее пример 4 (п.2.4), а также изучаемая
в теории линейного программирования
транспортная задача. Классическая
ее постановка выглядит следующим
образом.
Пусть имеются mзаводов
иnскладов. За
определенный период времениi– й завод производитsiединиц продукции,j– й склад может принятьdjединиц. Стоимость перевозки единицы
продукции с заводаiна складjравнаaij.
Требуется максимизировать количество
произведенной продукции и найти способ
ее перевозки на склады, имеющий
минимальную стоимость.
Все заводы могут произвести
единиц
продукции, а склады – принять единиц.
Понятно, что максимальное количество
производимой продукции равно минимальному
из этих двух чисел.
Если
обозначить fij- количество единиц продукции, перевозимых
с завода на склад , то стоимость всех
перевозок равна и нужно
найти величины fij,
доставляющие минимум выражению (2.9).
Данная задача может быть представлена
как задача поиска максимального потока
минимальной стоимости.
Рис 2.12
На рис. 2.12 приведена сеть для транспортной
задачи, в скобках – стоимость aijи пропускная способностьCijдуг. Вершиныз1,…,зmсоответствуют заводам, вершиныс1,…,сn– складам, добавлены фиктивный источникsи фиктивный стокt.
Для дуг(s,зi)установлена пропускная способностьsi,
для дуг(сj,t)–dj.
Это обеспечит выполнение ограничения
на количество продукции, производимой
на каждом заводе и потребляемой на
каждом складе. Для дуг вида(зi,сj)установлена стоимость передачи единицы
потокаaij.
Для решения задачи следует найти в этой
сети максимальный поток минимальной
стоимости. Тогдаfs,зi
будет означать количество продукции,
которую следует произвести на заводеi, fсj,t- количество продукции, потребляемой
складомj, аfзi,сj
- количество продукции, которую с
заводаiследует
перевезти на складj.
Насыщенным разрезом будет либо группа
дуг, исходящих изs(еслиV1V2),
либо группа дуг, заходящих вt(в противном случае).
Следует отметить, что стоимость передачи
единицы потока aijможет, вообще говоря, быть отрицательной.
Это возможно, если передача единицы
потока по дуге не требует расходов, а,
наоборот, приносит доход. Далее будут
рассмотрены соответствующие примеры.
Рис. 2.13
Ключевым для построения алгоритма
решения задачи (2.3) – (2.5) является понятие
увеличивающей цепи. Пусть в сети уже
имеется какой-либо поток, равный V.
Если на какой-либо дуге сетиfij<Cij, то поток на этой дуге может быть
увеличен на величину, не превосходящуюCij-fij. Поэтому поток в сетиVможет быть увеличен, если найдется путь
изsвt,
для всех дуг которогоfij<Cij.
По такому пути может быть пропущено
количество единиц потока, равное
минимальному из чиселCij-fijдля всех дуг пути. Это число можно
считать пропускной способностью пути.
Можно попытаться найти максимальный
поток в сети следующим образом: искать
путь с наибольшей пропускной способностью
и пропускать по нему максимально
возможное количество единиц потока,
продолжать это, пока такие пути
существуют. Однако легко убедиться,
что эта процедура не всегда приводит
к цели. Например, для графа на рис. 2.13
при первом поиске будет найден путь(s,2,3,t),
имеющий пропускную способность 5, и
если пропустить по нему 5 единиц потока,
то после этого в сети больше не будет
путей с положительной пропускной
способностью. Между тем максимальный
поток в этой сети равен 7, как это видно
из рис. 2.13 (числа на дугах – пропускная
способность, в скобках – поток).
Поэтому авторами алгоритма (Форд,
Фалкерсон) было введено более широкое
понятие увеличивающая цепь. Введем
в рассмотрение два множества дуг. ПустьI– множество дуг(i,j)сети таких, чтоfij<Cij.
На этих дугах поток может быть увеличен
наuij=Cij-fijединиц, поэтому они называютсяувеличивающими дугами. Далее,
обозначимRмножество
дуг таких, чтоfij>0.
На них поток может быть уменьшен наvij=fijединиц, это –уменьшающие дуги.
Очевидно, некоторые дуги могут
принадлежать обоим множествам. Рис
2.14
Цепь, соединяющую узлы sиt, будем называть
увеличивающей, если все
ее прямые дуги (ориентированные в
направлении от sкt)
принадлежат множествуI,
а все обратные дуги – множествуR.
Вдоль такой цепи может быть проведено
увеличение потока на количество единицv, равное минимальному
из чиселuijдля прямых дуг и чиселvijдля обратных. Для этого следует прибавитьvк потокамfijна прямых дугах, и вычестьvизfijна обратных дугах. Можно убедиться, что
при этом условия (2.7)-(2.8) для потока в
сети остаются выполненными. В самом
деле, для промежуточных вершин цепи
возможны четыре случая (рис 2.14). Если
обе смежные дуги цепи – прямые (узелi), то заходящий поток
увеличивается наv,
выходящий – тоже увеличивается наv.
Если одна из дуг прямая, а другая –
обратная, то либо заходящий (как для
узлаj) либо выходящий
(узелk) поток
увеличивается и уменьшается наv.
Если же обе дуги – обратные (узелl),
то заходящий поток уменьшается наv,
выходящий – тоже уменьшается наv.
Во всех случаях разность заходящего и
выходящего потоков не меняется и
остается равной нулю. Также можно
убедиться, что выходящий изsи заходящий вtпоток
увеличиваются наv,
независимо от того, какого типа дуги
являются смежными с этими узлами.
Если в сети проводить увеличение потока
не только вдоль путей, но и вдоль
увеличивающий цепей, то максимальный
поток рано или поздно будет найден.
Так, если в сети на рис. 2.13 при нулевых
потоках пропустить по пути (s,2,3,t)5 единиц, то после этого больше не будет
увеличивающих путей, но будет увеличивающая
цепь(s,3,2,t).
Опишем сначала алгоритм поиска
максимальной увеличивающей цепи. Он
основан на рассмотренном ранее методе
пометок. Пустьd(i)
- метка узла, в данном случае –
пропускная способность найденной
увеличивающей цепи в узелi,X– множество вершин.
Меткаl(i),
как и в алгоритме Дийкстры, вводится,
чтобы можно было найти последовательность
вершин, образующих увеличивающую цепь.
Шаг 1. Положить d(s)=,
d(i)=0
приis,l(i)=0,
X=
Шаг 2. Если tX,то СТОП: максимальная увеличивающая
цепь найдена.
Шаг 3. Если для всех iX
d(i)=0
,то СТОП: не существует увеличивающей
цепи в вершины, не входящие вX.
Иначе среди вершинiXнайти вершинуnс
максимальной меткой.
Шаг 4. Включить вершину nв множествоX, для
всехk
Xвыполнить:
Если в сети есть дуга(n,k)I(прямая, увеличивающая), то положитьd(k)=max{d(k), min{d(n),
Cnk-fnk}}.
Если при этом значениеd(k)изменяется, тоl(k)
положить равнымn.
Если в сети есть дуга(k,n)R(обратная, уменьшающая), то положитьd(k)=max{d(k),min{d(n),
fkn}}.
Если при этом значениеd(k)изменяется, тоl(k)
положить равнымn.
Перейти к шагу 2.
Если алгоритм заканчивает работу на
шаге 2, то по меткам , как в алгоритме
Дийкстры, может быть найдена увеличивающая
цепь, поток в сети может быть увеличен
по этой цепи на величину, равную метке
d(t).
Если же остановка происходит на шаге
3, то это означает, что в вершины,
включенные вX, есть
увеличивающие цепи, а в вершины, не
включенные вX, - нет.
То есть, для прямых дуг из вершинXв остальные вершиныfij=Cij,
а для обратных дугfij=0.
Значит, множествоXопределяет насыщенный разрез, и
максимальный поток найден.
Теперь можно описать алгоритм поиска
максимального потока. В нем, начиная
с нулевого потока, происходит
последовательнвй поиск увеличивающих
цепей и увеличение потока вдоль них,
пока это возможно.
Шаг 1. Положить fij=0для всехi,j=1,…,N.
Шаг 2. Определить множества дуг IиR. Выполнить алгоритм
поиска максимальной увеличивающей
цепи. Если она не найдена, то СТОП:
множествоXопределяет
насыщенный разрез.
Шаг 3. Провести увеличение потока вдоль
найденной цепи: добавить d(t)к потокамfijна прямых дугах, вычестьd(t)из потоковfijна обратных дугах. Перейти к шагу 2.
Если требуется найти не максимальный
поток, а поток заданной величины V,
то увеличение потока вдоль цепей следует
проводить, пока его величина не достигнетV. Насыщенного разреза
в этом случае может не быть. Если
максимальный поток будет найден раньше,
тоVединиц потока
пропустить через сеть невозможно.
Рис. 2.15
Рис. 2.16
Рис. 2.17
Пример 1. Применим данный алгоритм для
поиска максимального потока из вершины
1 в вершину 6 в сети на рис. 2.15. Числа у
вершин – метки d(i)после первого поиска увеличивающей
цепи. Поток может быть увеличен на 6
единиц, максимальная увеличивающая
цепь проходит через вершины (1,2,4,6).
Второй поиск приводит к результату на
рис. 2.16, поток увеличивается на 5 единиц
вдоль цепи (1,3,5,6). Далее, при последующих
итерациях алгоритма, поток увеличивается
вдоль цепи (1,2,4,3,5,6) на 3 единицы (рис.2.17),
вдоль цепи (1,2,3,4,5,6), содержащей обратную
дугу, на 1 единицу (рис.2.18). Наконец, при
следующем поиске увеличивающей цепи,
в множествоXпоследовательно включаются вершины
1,2,3,4, а у вершин 5 и 6 остаются нулевые
метки. Это означает, что увеличивающей
цепи нет, в сети найден максимальный
поток, множествоXопределяет насыщенный разрез (рис.
2.19). Максимальный поток в сети – 15
единиц.
Рис.
2.18 Рис. 2.19
С помощью данного алгоритма можно найти
не только максимальный поток в сети,
но и минимальный разрез. Это также может
быть полезным при решении ряда задач.
Пример 2. Города AиBсоединены между собой сетью автодорог,
проходящих еще через несколько населенных
пунктов. Для пресечения незаконной
торговли администрацией округа решено
построить на некоторых дорогах
контрольно-пропускные пункты (КПП), так
чтобы было невозможно проехать изAвB, минуя их все. Стоимость
содержания КПП для каждого участка
дорог известна. Где их нужно разместить,
чтобы минимизировать суммарную стоимость
содержания?
Для решения этой задачи нужно построить
сеть, в которой дуги соответствуют
различным участкам дорог, найти в ней
максимальный поток из AвB, считая стоимости
содержания КПП пропускными способностями
дуг. Насыщенный разрез определяет
множество дорог, на которых следует
построить КПП.
Рис. 2.20
В задаче о поиске потока минимальной
стоимости рассмотрим сначала случай,
когда все стоимости aijАлгоритм
решения задачи (3.6) – (3.8) для этого случая
построить сравнительно несложно. Пусть
для некоторой сети заданы пропускные
способности дугCijи стоимости передачи единицы потокаaij,
источникsи стокt
, все данные являются целочисленными.
Требуется найти максимальный поток
минимальной стоимости изsвt. Введем в рассмотрение
стоимостные метки узловp(i),
которые будут при выполнении алгоритма
равны стоимости, за которую поток может
быть передан изsвi. Еслиaijто
минимально возможная стоимость потока
в сети равна нулю, поэтому на первом
шаге всеp(i)=0.
За нулевую стоимость поток может быть
передан изsвt,
если есть увеличивающая цепь, состоящая
из дуг, для которыхaij.
Для всех узлов, для которых таких цепей
нет, следует увеличить стоимостные
метки и затем попытаться найти поток
большей стоимости. Например, для графа
на рис.3.10 (первое число на дуге –
стоимость, второе – пропускная
способность,s=1,
t=4) за нулевую
стоимость поток не может быть передан
из вершины 1 даже в соседние вершины 2
и 3, тем более – в 4. Значит, меткиp(i)вершин 2, 3 и 4 должны быть увеличены на
единицу. После этого будетp(1)=0,p(2)=1, а стоимость
передачи единицы потока по дуге(1,2)равна 1, так что есть возможность передать
3 единицы потока из вершины 1 в 2 за
стоимость, равнуюp(2)=1,
а метки вершин 3 и 4 следует увеличить
еще на 1, и так далее, пока не найдется
увеличивающая цепь изsвt. Таким образом,
увеличивающими и уменьшающими дугами
будут те дуги, для которыхaij=p(j)-p(i),
и множестваIиRувеличивающих и уменьшающих дуг должны
определяться следующим образом:
I = { (i,j) : aij=p(j)-p(i),
fij<Cij
} (2.10)
R = { (i,j) : aij=p(j)-p(i),
fij>0
} (2.11)
Эти множества дуг должны использоваться
в алгоритме поиска увеличивающей цепи,
а алгоритм поиска максимального потока
минимальной стоимости (Форд, Фалкерсон)
может быть описан следующим образом.
Шаг 1. Положить для всех i,j=1…N
fij=0,
p(i)=0.
Шаг 2. Определить множества дуг IиRпо правилам (2.10) –
(2.11).
Шаг 3. Найти при данных множествах I,
Rмаксимальную
увеличивающую цепь. Если она есть, то
провести увеличение потока и перейти
к шагу 2.
Шаг 4. (Увеличивающая цепь не найдена)
Если разрез, определяемый множеством
вершин X, полученным
при поиске увеличивающей цепи, является
насыщенным, то СТОП: найден максимальный
поток минимальной стоимости. Иначе для
вершинiXположитьp(i)равнымp(i)+1и перейти к шагу 2.
Итерация Стоимостная
метка Состояние
дуг Множество
X Увеличивающая
цепь Поток
p(1)
p(2)
p(3)
p(4)
(1,2)
(1,3)
(2,3)
(2,4)
(3,4) 0 0 0 0 0 - - - - - 1 - - 1 0 1 1 1 I - - - - 1,2 - - 2 0 1 2 2 I - I - - 1,2,3 - - 3 0 1 2 3 I - I - I 1,2,3,4 (1,2,3,4) 2 4 0 1 2 3 I,R - R - R 1,2 - - 5 0 1 3 4 I,R I - I R 1,2,3,4 (1,2,4) 1 6 0 1 3 4 R I - I,R R 1,3 - - 7 0 2 3 5 R I - I,R R 1,2,3,4 (1,3,2,4) 1 8 0 2 3 5 - R I,R I,R - 1 - -
Рис. 2.21
В таблице приведены результаты работы
алгоритма для графа на рис. 2.20, в последнем
столбце – пропускная способность
увеличивающей цепи. Конечный результат
приведен на рис 2.21. Максимальный поток
в сети равен 4 единицам.
Если требуется найти поток заданной
величины V, то в
алгоритме следует ввести соответствующее
условие остановки в шаге 3.
Пример. (Модель производственного
планирования Смита и Джонсона). Фирма
должна удовлетворить спрос на продукцию
в течение трех периодов. В каждом периоде
продукция может выпускаться в рабочее
и сверхурочное время. Заданы следующие
исходные данные:
Период
Производительность
(в единицах) Стоимость
производства единицы продукции
Ожидаемый спрос
(в единицах)
Рабочее время
Сверхурочное
время Рабочее
время
Сверхурочное
время 1 100 20 14 18 60 2 100 10 17 22 80 3 60 20 17 22 140
Стоимость хранения единицы продукции
на складе в течение одного периода
равна 1. Уровень запасов в начале первого
периода составляет 15 единиц. Определить
производственный план фирмы так, чтобы
минимизировать затраты.
Рис. 2.22
Данная задача может быть сформулирована
как задача о поиске максимального
потока минимальной стоимости. Сетевая
модель представлена на рис. 2.22. Дуги
(11,12)соответствуют первому периоду:
наличие на них потока вfijединиц означает, что в первый период
должно быть произведеноfijединиц продукции в рабочее время
(верхняя дуга) и в сверхурочное время
(нижняя дуга), дуги(21,22)соответствуют
второму периоду, дуги(31,32)– третьему.
Введен узел – источникs,
дуга(s,12)включена ввиду наличия на складе 15
единиц продукции. Дуги(12,22)и(22,32)означают возможность хранения продукции
на складе до конца второго и третьего
периодов, дуги(12,t),(22,t)и(32,t)соответствуют реализации продукции в
конце первого, второго и третьего
периодов. Для решения задачи в этой
сети следует найти максимальный поток
минимальной стоимости. На рис. 2.22
приведен конечный результат работы
алгоритма. В первый период следует
произвести 75 единиц продукции в рабочее
время. Вместе с имеющимися на складе
это составит 90 единиц. Из них 60 нужно
реализовать в первом периоде, а 30
оставить на складе. Во втором периоде
следует произвести 100 единиц в рабочее
время и 10 в сверхурочное, реализовать
80, 60 оставить на складе. Наконец, в третий
период нужно произвести 60 единиц в
рабочее время и 20 в сверхурочное, и
реализовать их вместе с 60 единицами,
хранившимися на складе. Суммарные
затраты при этом равны
aijfij
= 5990. Насыщенный разрез включает дуги(12,t),(22,t)и(32,t), то есть
спрос на продукцию может быть полностью
удовлетворен.
Задачи о поиске максимального
динамического потока в сети возникают
в тех случаях, когда для каждой дуги
сети (i,j)определено время передачи единицы
потока изiвjtij,
а также пропускная способностьCij– количество единиц потока, которые
могут передаваться по данной дуге
одновременно.
Пример 1. Туристическое агентство
обеспечивает доставку клиентов из
Москвы в Лас-Пальмас, используя как
прямые авиарейсы, так и транзитные.
Известно расписание регулярных рейсов
крупнейших авиакомпаний. Какое
максимальное количество туристов может
быть доставлено в пункт назначения в
течение недели?
Рассмотрим один из наиболее простых
случаев задачи о динамическом потоке.
Все исходные данные по-прежнему
предполагаются целочисленными, время
tтакже является
дискретным, времяtijпередачи единицы потока по дуге(i,j)
не зависит от момента начала передачи
и является постоянным. Таким образом,
если пропускная способность дуги равнаCij,то
в каждый из моментов времениt=0,1,2,…по ней можно отправлятьCijединиц потока изiвj , которые будут
прибывать вjв моментыtij,1+ tij,
2+ tij,….
В этом случае задача вполне аналогична
рассмотренной ранее задаче о поиске
потока минимальной стоимости при
неотрицательных стоимостях передачи
потока по дугам. В самом деле, минимальное
возможное время передачи потока из sвtравно нулю. За
нулевое время поток может быть передан
изsвt,
если есть увеличивающая цепь, состоящая
из дуг, для которых времяtij.
Для всех узлов, для которых таких цепей
нет, следует увеличить на единицу
временные метки, аналогичные стоимостным
меткам в предыдущем алгоритме, затем
попытаться найти поток за новое время
, и так далее. Следовательно, с помощью
алгоритма Форда и Фалкерсона можно
решить и задачу о поиске максимального
динамического потока. Для этого в
алгоритме стоимостиaijдолжны быть заменены временемtij.
Меткиp(i)будут означать максимальное время
передачи единицы потока в узелi.
Иначе будет выглядеть и конечный
результат работы алгоритма.
Рис.
2.23
Пример 2. Для графа на рис. 2.23 (первое
число на дуге – время, второе – пропускная
способность) найти максимальный
динамический поток из узла s=1в узелt=4за времяT=0,1,2, … .
В первой таблице приведены результаты
работы алгоритма. Первая увеличивающая
цепь появляется на четвертой итерации,
когда p(4)=4. Это
означает, что за время, меньшее четырех
единиц, ни одна единица потока не может
быть передана из1в4, за время4может быть передана одна единица
потока по пути1,2,3,4,для этого ее
надо отправить из начальной вершины 1
в момент времениt=0. Итерация Временная
метка Состояние
дуг
Множество X
Увел. цепь
Поток
p(1)
p(2)
p(3)
p(4)
1,2
1,3
2,3
3,2
2,4
3,4 0 0 0 0 0 - - - - - - 1 - - 1 0 1 1 1 I - - - - - 1,2 - - 2 0 1 2 2 I - I - -
1,2,3 - - 3 0 1 2 3 I - I - - - 1,2,3, - - 4 0 1 2 4 I - I - - I 1,2,3,4 1,2,3,4 1 5 0 1 2 4 I,R - R - - I,R 1,2 - - 6 0 1 3 5 I,R I - - - I,R 1,2,3,4 1,3,4 2 7 0 1 3 5 I,R I,R - - - R 1,2,3 - - 8 0 1 3 6 I,R I,R - - I - 1,2,3,4 1,2,4 3 9 0 1 3 6 R I,R - - I,R - 1,3 - - 10 0 2 3 7 - I,R R - I,R - 1,2,3,4 1,3,2,4 1 11 0 2 3 7 - I,R I - I,R - 1,3 - - 12 0 3 3 8 - I,R - - I,R - 1,3 - - 13 0 4 3 9 - I,R - I I,R - 1,2,3,4 1,3,2,4 1 14 0 4 3 9 - I,R - R I,R - 1,3 - -
Далее, при p(4)=5появляется еще одна увеличивающая цепь1,3,4, по ней может быть передано 2
единицы потока, время передачи по этой
цепи 3+2=5. При этом по пути1,2,3,4одна
единица потока может быть отправлена
в моментt=0и в
моментt=1, потому
что время передачи по этому пути равно
1+1+2=4. Таким образом, суммарная величина
потока, который может быть передан по
сети за времяT=5,
равна 1+1+2=4 единицам. Дальнейшие результаты
приведены во второй таблице.
Время T
Пути передачи
потока
Количество единиц
Моменты отправления
Всего передано
0,1,2,3
-
-
-
0
4
1,2,3,4
1
0
1
5
1,2,3,4
1,3,4
1
2
0,1
0
4
6
1,2,3,4
1,3,4
1,2,4
1
2
3
0,1,2
0,1
0
10
7
1,3,4
1,2,4
3
4
0,1,2
0,1
17
8
1,3,4
1,2,4
3
4
0,1,2,3
0,1,2
24
9
1,3,4
1,2,4
1,3,2,4
3
4
1
0,1,2,3,4
0,1,2,3
0
32
10
1,3,4
1,2,4
1,3,2,4
3
4
1
0,1,2,3,4,5
0,1,2,3,4
0,1
40
T>10
1,3,4
1,2,4
1,3,2,4
3
4
1
0,1,…,T-5
0,1,…,T-6
0,1,…,T-9
3*(T-4)+4*(T-5)+1*(T-8)=8T-40
Максимальный поток в сети получается
при p(4)=9, насыщенный
разрез определяется множеством вершинX={1,3}
На десятой итерации алгоритма при
p(1)=7увеличивающая
цепь содержит обратную дугу. По такой
цепи поток передаваться, конечно, не
может, а увеличение потока в сети вдоль
нее означает, что какое-то количество
единиц потока, ранее передававшихся
по возвратной дуге, теперь будут
передаваться по какой-то другой дуге.
Поэтому при записи решения во второй
таблице приT=7и
далеее приводятся пути, по которым
реально происходит передача потока, в
данном случае –1,3,4(3 единицы) и1,2,4(4 единицы).
В рассмотренном ранее алгоритме поиска
потока минимальной стоимости
предполагалось, что стоимости передачи
единицы потока по каждой дуге являются
неотрицательными.
Между тем во многих задачах, особенно
экономического характера, стоимость
может быть как положительной (расход),
так и отрицательной (доход). В некоторых
случаях возможно также ограничение
снизу на величину потока, передаваемого
по данной дуге. Таким образом, в общем
случае задача поиска потока минимальной
стоимости может быть сформулирована
следующим образом.
Величина lij0
называетсянижней пропускной
способностьюдуги(i,j).
Примеры:
1. Организаторы передвижной выставки
должны определить оптимальный маршрут
перемещения по нескольким городам.
Известна стоимость переезда между
городами и прогнозируемый доход (убытки)
для каждого города. Некоторые города
обязательно нужно посетить для выполнения
ранее подписанных контрактов.
В сетевой модели для этой задачи каждому
городу соответствует дуга со стоимостью,
равной доходу (убыткам) в данном городе,
нижней пропускной способностью, равной
1, если город обязательно нужно посетить,
и 0 в противном случае, и пропускной
способностью, равной 1. Возможным
переездам между городами соответствуют
дуги со стоимостью, равной стоимости
переезда, нижней пропускной способностью,
равной 0 и пропускной способностью,
равной 1. Должны быть добавлены вершины:
источник sи стокt.
Для решения следует передать одну
единицу потока изsвtза минимальную
стоимость. Путь передачи этой единицы
потока определяет оптимальный маршрут
передвижения выставки.
2. Три нефтеочистительных завода могут
получать неочищенную нефть из двух
месторождений. Стоимость одного галлона
нефти в этих месторождениях составляет
0.40$ и 0.30$ соответственно. Из обоих
месторождений нефть может поставляться
в неограниченном количестве, но не
менее 300000 галлонов в день. Производственная
мощность и затраты на ректификацию
одного галлона нефти для каждого из
заводов указаны в таблице.
Завод
Затраты на
ректификацию (долл/галл)
Максимальная
производительность (галлоны)
Минимальная
производительность (галлоны)
1
0.03
1250000
200000
2
0.04
1500000
300000
3
0.05
1350000
300000
Эти заводы должны снабжать нефтью
четыре района. Во второй таблице даны
затраты (в долларах) на транспортировку
одного галлона нефти.
Завод
Район 1
Район 2
Район 3
Район 4
1
0.05
0.06
0.06
0.07
2
0.06
0.07
0.07
0.06
3
0.07
0.06
0.06
0.05
Суточная потребность в нефти каждого
из районов и продажная цена одного
галлона приведены в третьей таблице.
Район
Минимальная
потребность
Максимальная
потребность
Продажная цена
(долл/галлон)
1
200000
250000
0.85
2
90000
175000
0.70
3
100000
175000
0.65
4
200000
350000
0.75 Поставки
Переработка
Транспортировка Продажа Рис.
2.24
Для максимизации своей прибыли нефтяная
компания должна поставлять в данные
районы нефть при минимальных затратах
на транспортировку.
Сетевая модель данной задачи приведена
на рис. 2.24, первое число на дугах –
стоимость ( единица – 10$), второе –
нижняя пропускная способность ( в
тысячах галлонов), третье – пропускная
способность. Для решения задачи
необходимо найти максимальный поток
минимальной стоимости из вершины 1 в
14.
Для решения задачи (2.12) – (2.14) прежний
алгоритм не годится по двум причинам.
Во-первых, неизвестна минимальная
возможная стоимость передачи единицы
потока. Во-вторых, начальный нулевой
поток в сети может оказаться недопустимым,
то есть не удовлетворяющим условию
(2.14), если есть lij0.
Поэтому для данной задачи был разработан
другой алгоритм, который носит названиеалгоритма дефекта. Перейдем к его
описанию.
Добавим в сеть дополнительную дугу
(t,s),
соединяющую вершину-стокtи источникs,и
будем предполагать, что по ней протекает
поток величиныV, то
есть весь поток, попадающий в стокt,
возвращается по этой дуге обратно вs.
Такой замкнутый поток в новом графе
называетсяциркуляцией. Теперь для
вершинsиtвеличины заходящего и выходящего потока
равныV, поэтому может
быть сформулированазадача о поиске
циркуляции минимальной стоимости:
Для данного потока в сети { fij
}величина потока изsвtпри этом равнаV=fts.
Обе задачи о поиске потока минимальной
стоимости могут быть сведены к задаче
о поиске циркуляции минимальной
стоимости путем подходящего выбора
параметров возвратной дуги(t,s)следующим образом:
1. Если требуется найти поток заданной
величины V, имеющий
минимальную стоимость, то следует
положитьats=0,
lts=V,
Cts=V.
Любой допустимый поток тогда будет
иметь величинуV.
2. Если нужно найти максимальный поток
минимальной стоимости, то следует
положить ats=-M,
lts=0,
Cts=,
гдеM– очень большое
число. Добавление каждой единицы потока
на дуге(t,s)приведет тогда к уменьшению суммарной
стоимости наM, то
есть оптимальное решение будет при
максимальном потоке.
Для вершин графа введем опять стоимостные
метки p(i),
i=1,…,N.
При поиске решения задачи (2.6) – (2.8) с
помощью алгоритма Форда-Фалкерсона
было видно, что потокиfijна дугах удовлетворяют следующим
условиям:
fij=0
, если aij>p(j)-p(i), 0fijCij
, если aij=p(j)-p(i), fij=Cij
, если aij<p(j)-p(i).
Если обозначить qij=aij-(p(j)-p(i))=
aij-p(j)+p(i),то в общем случае эти условия выглядят
следующим образом: fij=lij
, еслиqij>0,(2.18)
lijfijCij
, еслиqij=0, (2.19) fij=Cij
, еслиqij<0. (2.20)
С помощью теории линейного программирования
можно показать, что циркуляция в графе
имеет минимальную стоимость тогда и
только тогда, когда выполнены условия
(2.18) – (2.20). В задаче (2.15) – (2.17), являющейся
задачей линейного программирования,
они представляют собой условия
дополняющей нежесткости, которые
являются необходимыми и достаточными
условиями минимума.
Таким образом, задача будет решена,
если удастся найти циркуляцию {fij}и стоимостные меткиp(i),
удовлетворяющие условиям (2.16) – (2.20).
Идея алгоритма дефекта состоит в
следующем. Пусть для дуг сети определены
потоки fij,
удовлетворяющие условию (2.16), а для
вершин – стоимостные меткиp(i).
Например, в начале они все могут быть
равны нулю. При этом условия (2.17) –
(2.20) могут быть не выполнены. Для каждой
дуги определяется величинадефекта.
Дефект равен нулю, если условия (2.17) –
(2.20) выполнены, и положителен в противном
случае. Если в сети есть дуги с
положительным дефектом, выбирается
одна из них(i,j),
и для нее делается попытка устранить
дефект. Для этого поток на дуге должен
быть или увеличен, или уменьшен. Если
поток требуется увеличить, то это можно
сделать в том случае, если такое же
количество единиц потока возможно
передать по остальным дугам сети, не
увеличивая их дефекта. Если изjвi имеется
увеличивающая цепь, то увеличение
потока на(i,j)производится, в противном случае
происходит изменение метокp(i).
Если же поток на(i,j)нужно уменьшить, то производится поиск
увеличивающей цепи изiвj, чтобы направить
его другим путем. Оптимальное решение
будет найдено, если дефекты всех дуг
удастся сделать равными нулю. Однако
в сети с положительными нижними
пропускными способностями допустимый
поток может вообще не существовать.
Определим понятие дефекта дуги. Во
втором столбце таблицы приводятся
девять различных случаев состояния
дуги, для каждого из которых в третьем
столбце определяется величина дефекта.
Как и ранее, вводятся множества IиRдуг, на которых
можно увеличивать и уменьшать поток.
В последнем столбце – максимальное
количество единицvij,
на которое может быть увеличен (для дуг
изI) или уменьшен (R)
поток.
Состояние дуги
Дефект Kij
Множество
vij
1
qij<0,
fij<Cij
qij(fij-Cij)
I
Cij-fij
2
qij<0,
fij=Cij
0
-
-
3
qij<0,
fij>Cij
fij-Cij
R
fij-Cij
4
qij=0,
fij<lij
lij-fij
I
Cij-fij
5
qij=0,
lijfijCij
0
I,
если
fij<Cij
,
R,
если
fij>lij
увел. на Cij-fij,
умень. на
fij-lij
6
qij=0,
fij>Сij
fij-Cij
R
fij-Cij
7
qij>0,
fij<lij
lij-fij
R
lij-fij
8
qij>0,
fij=lij
0
-
-
9
qij>0,
fij>lij
qij(fij-lij)
R
fij-lij
Теперь можно привести описание алгоритма
дефекта.
Шаг 1. Положить
fij=0,
i,j=1,…,N, q(i)=0, i=1,…,N.
Шаг 2. Для всег дуг сети вычислить дефект
Kij.
Если все они равны нулю, то СТОП: найден
поток минимальной стоимости.
Шаг 3. Определить множества дуг IиR. Выбрать дугу(i,j),для которойfij<lij, если такой нет – то любую дугу с
положительным дефектом. Если она
принадлежитI, то на
следующем шаге считать вершинуjисточникомs, аi– стокомt, еслиR– считатьiисточникомs, аj– стокомt.
Шаг 4. Найти максимальную увеличивающую
цепь из sвt.
Если ее нет, то перейти к шагу 5. Иначе
провести увеличение потока вдоль цепи,
но не более, чем наvstединиц. Соответственно изменить поток
на дуге(s,t)(увеличить, если она из множестваI,
уменьшить, если изR).
Перейти к шагу 2.
Шаг 5. Пусть X–
множество вершин, определяющее разрез
при поиске увеличивающей цепи на шаге
4,tX.
Определить множества дуг:A1
= { (i,j):
iX,
jX,
qij>0,
fij<Cij
}A2 = {
(i,j):
jX,
iX,
qij<0,
fij>lij}
Вычислить:
Если , то
СТОП: если поток допустимый, то найдено
решение, в противном случае допустимый
поток не существует. Иначе для всехiXположитьp(i)равнымp(i)+и перейти к шагу 2.
На первом шаге устанавливаются начальные
нулевые значения потока и стоимостных
меток, на втором вычисляются дефекты
дуг. На третьем шаге определяется
принадлежность каждой дуги множествам
IиR,
и выбирается дуга, для которой далее
будет сделана попытка уменьшить дефект,
причем в первую очередь следует выбирать
те дуги, для которых не выполнено
ограничение (2.17). Дуга с положительным
дефектом всегда принадлежит либо
множествуI, либоR,
но не обоим сразу. Чтобы устранить
дефект, поток на дуге(i,j)надо увеличить (если она принадлежитI) или уменьшить (если
она принадлежитR). В
первом случае поток должен быть
“возвращен” обратно изjвi, во втором – передан
изiвjкаким-либо другим путем. В обоих случаях
для этого на шаге 4 ищется увеличивающая
цепь. Если она есть, то поток на ней и
на дуге(i,j)изменяется так, чтобы максимально
уменьшить или совсем устранить деефект
на этой дуге. Если же увеличивающей
цепи нет, то на шаге 5 происходит изменение
стоимостных метокp(i).A1– множество
прямых дуг разреза,- минимальное количество единиц, на
которое следует увеличить все меткиp(i)вершин, не принадлежащихX,
чтобы какая-либо из них вошла в множествоX. Аналогично,A2- множество обратных дуг разреза,- минимальное количество единиц, на
которое следует увеличить все меткиp(i)вершин, не принадлежащихX,
чтобы какая-либо из них вошла в множествоX. Поставки
Переработка Транспортировка
Продажа
Рис.
2.25
На рис. 2.25 приведен результат работы
алгоритма дефекта для задачи примера
2 (п.2.5.5.). В сеть добавлена возвратная
дуга (14,1)с стоимостью–100(большое числоM=100),
нижней пропускной способностью0и пропускной способностьютак как требуется найти максимальный
поток минимальной стоимости. Следует
заметить, что конечные стоимостные
метки зависят от порядка выбора дефектных
дуг на шаге 3, и поэтому могут отличаться
на константу от меток на рис. 2.25.
Как
выполняется обход вершин и ребер графа
? Как
проводится поиск в глубину при заданных
смежных вершин ? В
чем заключается задача раскраски графа
? Какая
раскраска графа называется правильной
? В
чем состоит алгоритм минимальной
раскраски ? Какие
существуют оценки хроматического
числа ? Как
формируется задача построения
кратчайшего остовного дерева (остова
минимального веса) ? В
чем заключается алгоритм Краскала ? Как
формируется задача поиска путей между
двумя вершинами графа ? В
чем заключается алгоритм Дийкстры ? Чем
отличаются алгоритмы Форда и Дийкстры
? В
чем заключается алгоритм Флойда ? Как
формулируются потоковые задачи ? Как
определить поток в цепи ? Как
формулируется задача поиска максимального
потока в сети ? Как
формулируются задачи поиска потока
минимальной стоимости и максимального
потока минимальной стоимости? В
чем заключается алгоритм поиска
максимальн В
чем заключается алгоритм поиска
максимального потока ? В
чем заключается алгоритм поиска потока
минимальной стоимости? Какие
алгоритмы используются для решения
задач о динамических потоках ? В
чем заключается сущьность алгоритма
дефекта ?
Является
ли граф Петерсена гамильтоновым ?
2.
Существует ли в графе G2
эйлеровы цепи и циклы ? Нарисовать граф.
3.
Доказать, что в графе без вершин с
нулевой полустепенью исхода (захода)
имеется простой контур.
4.
Доказать, что число различных деревьев,
которые можно построить на М вершинах,
равно ММ-2
.
5.
Пусть G-граф,
множество вершин которого совпадает
с отрезком натурального ряда (1,2,3,…,n),
а множество ребер определяется так:
несовпадающие сершины U
и V
смежны тогда и только тогда, когда числа
U
и V
взаимно простые. Требуется :
а)
записать матрицу S;
б)
показать, является ли граф G
связным ?
6.
Найти компоненты сильной связности
графа G1:
7.
Является ли граф G
планарным ? Доказать.
8.
Построить подграф графа G,
порожденный вершинами
9.
Доказать, что графы (а) изоморфны, а
графы (б) неизоморфны:
а)
б)
10.
Сориентирвать граф G5:
11. Найти
,,Ʋ графаG6:
12.
Определить степень связности графа
G7:
13. В
графе G1найти
минимальный путь из вершиныV1
в вершинуV7.
14.
Определить минимальный путь из V1
вV7во
взвешенном орграфеG3,
имеющим матрицу длин дугL:
15. Найти
хроматическое число графа G2.
16. В изображенном
на рис. 3.1 графе параметры дуг соответствуют
верхним границам потоков по ним. Найти:
а) цепь с максимальной
пропускной способностью из узла 1 в
узел 8;
б) максимальный
поток из узла 1 в узел 9;
в) максимальный
поток между всеми парами узлов.
Рис. 3.1
17.
Мебельная фабрика производит обеденные
столы. Изготовление стола состоит из
трех основных этапов: сборка, окраска,
сушка. Сборка может производиться в
одном из цехов A,B или C, окраска - в одном
из цехов B,C,D или E ( но не в том же, в
котором производится сборка ), сушка -
в цехе F. Поскольку цеха оснащены
различным оборудованием, то время
выполнения операций в них не одинаковое.
Средняя продолжительность ( в минутах
) выполнения каждой операции приводится
в таблице. Цех A B C D E F Сборка 55 62 66 - - - Окраска - 45 35 50 40 - Сушка - - - - - 60
Во
второй таблице дано время перевозки
продукции между цехами:
A B C D E F A - 14 11 12 18 15 B 14 - 7 10 8 12 C 11 7 - 5 6 22 D 12 10 5 - 14 5 E 18 8 6 14 - 10 F 15 12 22 5 10 -
Требуется
определить, в каких цехах должна
выполняться каждая из операций, чтобы
среднее время изготовления стола было
минимальным.
18.
Компания TransAuto должна отправить колонну
грузовиков из города 1 в город 11 по
одному из маршрутов, проходящих через
города 2,3,...,10. Длина автодорог, имеющихся
между городами ( в милях ), дана в таблице.
1
2
3
4
5
6
7
8
9
10
11
1
75
116
2
85
92
3
35
70
4
85
55
68
5
60
32
52
100
6
110
88
7
105
8
90
9
10
100
Все
дороги с двусторонним движением, но не
являются равноценными. Через города
...8,4,5,10,... проходит автомагистраль
первого класса, через города ...2,4,9,6,...
– магистраль второго класса. Грузовик
расходует 6 галлонов бензина на 100 миль
пути на дороге 1 класса, 8 галлонов - на
дороге 2 класса, 12 галлонов - на остальных
дорогах. Стоимость 1 галлона бензина -
6 долларов. Плата за проезд по дороге 1
класса - 10 $ с каждой машины, по дороге
2 класса - 5 $ ( возможен бесплатный переезд
с дороги 1 класса на дорогу 2 класса ).
Кроме того, на дороге, соединяющей
города 4 и 9, имеется мост, проезд по
которому стоит 6 $ с машины.
Какой
маршрут должна выбрать компания, чтобы
свести к минимуму свои расходы?
19. В
одном из сельских районов имеется 7
ферм и 2 элеватора, соединенных между
собой сетью автодорог. В таблице указаны
длины дорог, соединяющих эти объекты.
На некоторых из дорог имеются мосты,
пропускная способность которых указана
в скобках. Во второй таблице указана
производительность каждой фермы.
Ф2 Ф3 Ф4 Ф5 Ф6 Ф7 Э1 Э2 Ф1 30 21
Ф2
12
17(5)
Ф3
18
36(9)
Ф4
16(20) 10(30)
Ф5
21(8) 26(20) Ф6
27(4)
11(12)
Ферма Ф1 Ф2 Ф3 Ф4 Ф5 Ф6 Ф7 Производительность 6 10 12 12 8 9 6
Свою
продукцию фермеры должны отвозить на
элеваторы, однако они не имеют возможности
вывезти весь произведенный продукт в
виду ограниченноц пропускной способности
мостов. Местный бюджет позволяет
произвести капитальный ремонт одного
моста. Какой из мостов следует
отремонтировать ( и на сколько увеличить
его пропускную способность ), так чтобы
фермеры могли подъезжать к элеватору
по возможности более короткими путями?
20.
Федеральное управление автомобильных
дорог планирует строительство дорог,
которые должны связать между собой
девять городов. Все города должны быть
связаны между собой, причем для каждой
пары городов дорога, связывающая их,
должна проходить не более чем через
два других города. Затраты на строительство
дорог приводятся в таблице. Какие дороги
следует построить?
1 2 3 4 5 6 7 8 9 1 - 22 24 16 41 38 62 63 23 2
- 19 23 26 42 43 52 37 3
- 14 20 28 30 33 33 4
- 36 22 40 39 17 5
- 43 18 31 58 6
- 34 27 25 7
- 13 64 8
- 53
21.
Проект исследований и научно-технических
разработок состоит из четырех задач:
A,B,C,D, темпы решения которых зависят от
выделенной для этой цели суммы. В таблице
указано время выполнения задачи в
месяцах ( первое число ) и стоимость в
тысячах долларов ( второе число ).
Темп A B C D Низкий 6,6 5,8 6,2 7,10 Средний 4,8 3,9 3,3 5,12 Высокий 3,9 2,10 1,5 3,18
Требуется
определить:
1. За какое наименьшее
время может быть выполнен проект, если
на его осуществление может быть выделено
35000 $ ?
2.
В какую минимальную сумму обойдется
проект, если его необходимо выполнить
не позднее, чем за 18 месяцев ?
С
семи платформ, находящихся в море, к
конечной станции нефтепровода,
находящейся на берегу, перекачивается
неочищенная нефть по системе
трубопроводов, соединяющих между собой
платформы. Пропускная способность
каждого трубопровода указана в матрице.
В последнем столбце - производительность
каждой скважины.
1 2 3 4 5 6 7 Станция Произв. 1
8 10
15 2
8
16
17 3
30
14 4
15
21
6 5
15 14
12 6
40 11 7
50 5 Управляющий
станцией должен дать указание, по каким
трубопроводам должна перекачиваться
нефть, чтобы вся она могла быть доставлена
на станцию, однако ему никак не удается
это сделать. Возможно ли это вообще?
Если нет, то пропускную способность
какого трубопровода (но только одного!)
следует увеличить и на какую величину,
чтобы задача стала выполнимой?
23.
Семь городов используют единую систему
связи. Каждый элемент таблицы равен
максимальному числу вызовов, которые
одновременно могут обслуживаться
линией, соединяющей соответствующую
пару городов.
1 2 3 4 5 6 7 1
9
11
4 2
7
3 10
3 9 7
4
8 2 6 5 11 3
8
6 6
10
2
Для
каждой пары городов найти максимальное
число вызовов, которые могут обслуживаться
одновременно. На какой из линий следует
увеличить количество каналов (т.е.
одновременно обслуживаемых вызовов),
чтобы чтобы наибольшее количество пар
городов улучшили возможность связи
между собой?
24.
Четыре шахты поставляют каменный уголь
пяти газоперерабатывающим заводам.
Расходы на транспортировку угля,
задаваемые матрицей стоимостей (в тыс.
долл.), включают плату за его перевозку
по железным и автомобильным дорогам,
а также плату за погрузочно-разгрузочные
работы.
Завод
1 2 3 4 5 Предложение Шахта 1 9 10 8 9 7 500 2 4 8 12 7 9 900 3 6 3 4 2 8 700 4 7 6 5 4 3 600 Спрос 400 700 400 500 700
Построить
схему транспортировки угля, имеющую
минимальную стоимость.
25.
Компания осуществляет перевозку товаров
с двух складов А и B в магазины C, D и E.
Поскольку товары являются скоропортящимися,
их нужно доставлять точно в срок,
указанный заказчиком. В рассматриваемый
день компания имеет заказы на выполнение
следующих рейсов:
Откуда
Куда
Срок выполнения
Ожидаемая прибыль
1
A
C
7-45
370
2
B
E
8-15
510
3
B
E
9-30
720
4
A
D
10-15
800
5
A
D
11-15
860
6
A
E
11-45
620
7
B
C
12-15
700
8
A
E
13-15
410
9
B
D
14-00
460
Компания
располагает двумя грузовиками. Во
второй таблице задано время передвижения
между складами и магазинами в минутах,
а также расходы при проезде между
объектами без груза (в скобках).
Гараж A B C D E Гараж
15(30) 30(40)
A
30 90 60 B
60 45 30 C (70) 90(90) 30(40)
D (60) 60(80) 45(60)
E (70) 45(50) 30(40)
Составить
расписание перевозок, которое давало
бы компании наибольшую прибыль.
26.
Фирма должна удовлетворить спрос на
продукцию в течение пяти периодов.
Заданы следующие исходные данные:
Период Производительность
(в единицах) Стоимость
производства единицы продукции Спрос
в единицах 1 100 14 60 2 90 15 80 3 60 17 120 4 80 18 50 5 50 20 50 Стоимость
хранения единицы продукци на складе в
течение одного периода равна 1 долл.,
однако если она хранится более одного
периода, то стоимость хранения возрастает
на 1 $ в каждый последующий период.
Уровень запасов в начале первого периода
составляет 50 единиц.
Составить
производственный план на пять периодов,
минимизирующий расходы фирмы.
27.
Компания, изготавливающая лыжи, имеет
три фабрики A,B, и C. Стоимость изготовления
одной пары лыж, не считая стоимости
древесины, а также максимальная месячная
выработка известны: для фабрики A: 15 $
и 2500 пар, для B - 20 $ и 4000, для C - 10 $ и
4800.Kомпания получает древесину у двух
поставщиков по цене 50 центов за фунт у
первого и 40 у второго. На изготовление
одной пары лыж идет 8 фунтов
древесины.Затраты на транспортировку
одного фунта древесины от поставщиков
на фабрики равны: для первого: 1,2 и 3 $ на
A,B,C соответственно, для второго - 4,3 и
2.
Компания
продает свою продукцию главным образом
в трех городах: X,Y и Z. Для каждого из
них известна продажная цена единицы
товара - 90 $, 75 $ и 100 $, и предполагаемый
спрос - 7000,4000 и 4500 в месяц для городов
X,Y и Z соответственно. Затраты на
транспортировку единицы продукции с
фабрик в города приводятся в таблице:
X Y Z A 2 2 3 B 3 5 6 C 2 1 4 Составить
для компании производственный план:
установить, где следует закупать
древесину каждой фабрике, сколько пар
лыж на ней изготавливать и куда отправлять
продукцию, чтобы компания имела
максимальную прибыль.
28.Фирма имеет заказы
на выполнение десяти заданий, каждое
из которых может выполнить один рабочий.
Моменты начала и завершения выполнения
каждого задания, а также отрезки времени,
необходимые для перехода с одних рабочих
мест на другие ( в минутах ) приведены
в таблице.
Начало
Конец
1
2
3
4
5
6
7
8
9
10
1
13-00
13-30
-
60
10
230
180
20
15
40
120
30
2
18-00
20-00
10
-
40
75
40
5
30
60
5
15
3
22-30
23-00
70
30
-
0
70
30
20
5
120
70
4
16-00
17-00
0
50
75
-
20
15
10
20
60
10
5
16-00
19-00
200
240
150
70
-
15
5
240
90
65
6
12-00
13-00
20
15
20
75
120
-
30
30
15
45
7
14-00
17-00
15
30
60
45
30
15
-
10
15
0
8
23-00
24-00
20
35
15
120
75
30
45
-
20
10
9
20-10
21-00
25
60
15
10
100
70
80
60
-
120
10
13-45
15-00
60
60
30
30
120
40
50
60
70
-
Директору
фирмы, чтобы принять заказ, необходимо
знать минимальное количество рабочих,
которые могут выполнить все задания.
29.
Владелец магазина приобрел 90 телевизоров,
заплатив 40 $ за каждый. Ему известна их
прогнозируемая продажная цена для
каждого из последующих пяти периодов
времени. Кроме того, изменяются затраты
на хранение товара. Данные приведены
в таблице.
Количество
телевизоров 0-20 21-50 51-80 более
80 Затраты
на хранение одного телевизора период
1 2.80 2.50 2.30 2.00 период
2 4.00 3.60 3.30 3.00 период
3 3.50 3.20 2.90 2.60 период
4 3.60 3.30 3.00 2.50 Продажная
цена одного телевизора период
1 100 96 92 85 период
2 98 94 90 87 период
3 108 102 96 90 период
4 104 100 92 88 период
5 112 106 100 90
Сколько
телевизоров нужно продать в каждый из
периодов, чтобы максимизировать прибыль?
30.
Нефтяная компания Black Gold Petroleum должна
построить нефтепровод, соединяющий
месторождение M с одним из
нефтеперерабатывающих заводов F1 или
F2. Перекачка нефти осуществляется при
помощи насосных станций, которые должны
отстоять друг от друга не более чем на
100 миль и могут располагаться в населенных
пунктах 1,...,8. В таблице даны расстояния
между всеми объектами в милях, а также
стоимость строительства насосной
станции в каждом из пунктов в тысячах
$ (в последнем столбце). Стоимость одной
мили нефтепровода равна в среднем
72000$.
M
1
2
3
4
5
6
7
8
F1
F2
M
-
73
140
188
60
81
130
196
207
260
257
1
-
71
119
49
104
102
138
165
202
216 2120
2
-
78
80
103
48
74
98
134
142 1970
3
-
135
173
110
58
111
83
113 2400
4
-
56
69
131
145
205
202 1850
5
-
70
146
140
223
206 1470
6
-
80
74
150
139 1790
7
-
50
70
67 2230
8
-
109
71 1650
|F1
-
53
F2
-
Как следует
проложить нефтепровод?
31.
Предприятия, производящие водные лыжи,
имеют четыре общегосударственные
оптовые базы, с которых лыжи распределяются
по пяти различным магазинам. Найти
схему транспортировки лыж, имеющую
минимальную стоимость, при условии,
что базы располагают 120,200,330,400 парами
лыж, а магазинам требуется 200,250,300, 100 и
150 пар сответственно. Затраты на
транспортировку задаются матрицей
стоимостей.
Магазины 1 2 3 4 5 1 5 7 3 15 9 2 6 2 8 5 6 3 3 9 8 2 2 4 7 6 8 7 4
32.
Цех получил срочный заказ на изготовление
некоторого изделия. Процесс его
изготовления включает 8 последовательных
операций, каждая из которых может быть
выполнена на одном из трех станков А,B
или C.В первой табдице дано время
выполнения каждой операции (в минутах),
Операция
1 2 3 4 5 6 7 8 A 65 140 35 65 95 15 30 20 B 75 120 60 50 80 40 40 15 C 90 110 45 45 45 20 25 25 во
второй - время переналадки станка для
выполнения последующих операций для
станка А (первое число), B (второе) и C
(третье).
2
3
4
5
6
7
8
1
10,5,10
130,9,20
20,35,15
12,13,15
55,60,40
20,10,5
10,10,15
2
8,10,12
12,15,10
35,15,10
25,25,20
30,35,60
18,15,60
3
5,10,6
10,12,4
15,20,30
5,8,10
15,10,5
4
30,25,30
55,60,70
5,10,5
20,30,25
5
12, 3,7
10,12,8
35,45,40
6
10,10,0
5,5,8
7
10,15,5
Каково минимальное
время изготовления изделия?
33.
Десять городов связаны между собой
линиями связи, состоящими из различного
числа телефонных каналов. Каждая линия
имеет ограниченную надежность и может
иногда выходить из строя на непродолжительное
время. В таблице задано количество
телефонных каналов на каждой линии
(первое число), а также вероятность ее
отказа (в процентах, второе число).
1 2 3 4 5 6 77 8 9 10 1
15,1
12,3 20,1
2
25,2 10,2
3
18,5
16,1 10,1
4
30,2
20,2
5
25,8 8,2
6
20,1
20,1
7
18,2 15,4 5,2 8
24,3 9
18,4
Фирма,
расположенная в городе 1, для постоянной
связи с филиалом, расположенным в городе
10, должна иметь в распоряжении пучок
из 15 телефонных каналов прямой связи.
На каких линиях ей следует арендовать
каналы, тобы: 1) пучок имел бы не более
4 промежуточных центров коммутации (в
данном случае городов, кроме конечных
1 и 10) и 2) Вероятность блокировки связи
была минимальной?
34.
Добываемый уран перевозится с рудника
на три завода A,B,C, где он обогащается,
в результате чего образуется
высокорадиоактивное вещество
шестифтористый уран. Затем его доставляют
десяти предприятиям, на которых оно
должно быть преобразовано в топливо
для ядерных реакторов. Правительство,
исходя из соображений безопасности,
разработало десятибалльную шкалу,
характеризующую степень риска при
транспортировке шестифтористого урана
по различным маршрутам (число 10
соответсовует наибольшему риску).
Соответствующие значения, а также
требуемый объем поставок (кг в день) на
каждое из 10 предприятий, приводятся в
таблице.
1
2
3
4
5
6
7
8
9
10
A
9
8
7
4
6
3
8
6
5
2
B
1
7
9
10
8
3
6
7
5
4
C
3
3
5
7
7
8
9
1
2
3
Спрос
100
100
300
150
200
90
110
50
50
100 Заводы
могут производить шестифтористый уран
в количествах 600 кг (А), 400 кг (B), 500 кг (C)
в день. Найти схему транспортировки,
при которой общий риск минимален.
35.
На линии последовательной сборки
имеется 6 рабочих мест, на которые
необходимо назначить рабочих. Имеется
9 кандидатов на эти вакантные места.
Администрации предприятия известна
квалификация каждого рабочего и,
следовательно, она может оценить
эффективность его работы на каждом
рабочем месте. Данные приведены в
таблице.
Рабочее
место
1 2 3 4 5 6 1 3 4 2 7 8 0 2 6 10 0 0 4 0 3 6 9 4 4 10 0 4 0 0 6 7 8 9 5 10 8 3 0 6 5 6 0 6 2 0 4 0 7 9 6 9 0 0 4 8 6 0 0 3 5 0 9 4 5 0 0 2 0 Эффективность
работы всего конвейера определяется
минимальной из эффективностей работы
на каждом из мест. Какое назначение
должна сделать администрация, чтобы
эффективность работы конвейера была
максимальной?
36.
Программа обучения в бизнес-школе
включает 11 дисциплин: A, B, C, D, E, F, G, H, I,
J, K. Однако для получения диплома не
обязательно изучать их все, достаточно
изучить последовательно несколько
дисциплин в одном из следующих порядков:
A, D, H; A, E, G, I; A, F, I; B, C, G, I; B, J или B, C, K, H. В
таблице приведены максимальное
количество слушателей, которые
одновременно могут изучать данную
дисциплину, а также стоимость обучения.
Продолжительность обучения для каждой
дисциплины - 1 месяц.
Дисциплина
Количество
Стоимость
A
30
50
B
20
80
C
10
10
D
10
60
E
20
20
F
30
60
G
40
20
H
15
40
I
50
10
J
20
90
K
20
10
1) Какое максимальное
количество слушателей могут быть
обучены за 6 месяцев? 2) Тот
же вопрос при условии, что никто из них
не желает платить за обучение более
120 $.
37.
Фирма Dog's Tail владеет четырьмя заводами,
производящими летающие сковородки.
Себестоимость продукции и цены на сырье
для различных заводов не одинаковые.
В данном районе имеется пять пунктов
сбыта продукции, в каждом из них
установлены свои цены на продукцию.
Завод
1
2
3
4
Производственная
мощность (тыс. единиц продукции)
200
250
325
150
Затраты на
производство единицы продукции
20
25
19
20
Стоимость сырья
10
9
12
8
Транспортные
затраты на единицу продукции
Товарооборот(тыс.)
Цена
Пункты сбыта
1
4
10
12
19
130
40
2
3
7
5
6
160
42
3
5
9
4
7
200
41
4
7
5
9
3
150
42
5
6
8
7
6
210
41
Требуется определить
оптимальный план производства и
распределения продукции.
38.
East Texas Freight Company (EFTC) производит перевозки
автотранспортом крупногабаритного
оборудования. EFTC предлагают заключить
контракт о перевозке неупакованного
груза между семью предприятиями НАСА
в г. Хьюстоне, штат Техас. По этому
контракту требуется перевозить несколько
видов оборудования с большим вертикальным
габаритом. EFTC определила минимальную
высоту проезда под мостами и надземными
коммуникациями для каждой из дорог,
соединяющих предприятия. Эти данные
приведены в таблице (0 - нет прямой
дороги).
1 2 3 4 5 6 7 1 - 11 30 0 0 0 14 2 11 - 0 12 15 0 0 3 30 0 - 20 9 13 0 4 0 15 0 - 10 14 0 5 12 0 9 10 - 0 0 6 0 0 20 14 0 - 0 7 14 0 0 18 0 9 -
Требуется
определить максимальную возможную
высоту груза для каждой пары предприятий
и маршруты для перевозок.
39.
Восемь вычислительных центров (ВЦ)
связаны между собой цифровыми каналами
связи в единую информационно-вычислительную
сеть. Пропускные способности каналов
(кб/сек) даны в таблице.
1 2 3 4 5 6 7 8 1 - 96 - 128 256 - 64 - 2 96 - 2048 64 512 96 - - 3 - 2048 - - 192 192 - 512 4 128 64 - - - - 128 - 5 256 512 192 - - - 256 256 6 - 96 192 - - - - 128 7 64 - - 128 256 - - - 8 - - 512 - 256 128 - -
Для
обеспечения требуемого уровня надежности
связи между двумя ВЦ необходимо, чтобы
маршрут передачи информации проходил
не более чем через два промежуточных
узла. ВЦ обмениваются пакетами данных
сравнительно редко, но объем передаваемой
за один сеанс информации может быть
велик, поэтому желательно, чтобы путь
передачи информации имел бы как можно
большую пропускную способность.
Какие маршруты
следует выбрать для обмена данными
между каждой из пар ВЦ?
40.
Таможенная полиция подозревает, что
между городами A и B, расположенными по
разные стороны государственной границы,
осуществляется контрабандная торговля.
Города соединены между собой сетью
автомобильных дорог, проходящих также
через города C...L. Для пресечения
незаконной торговли полиция предполагает
разместить на некоторых дорогах
контрольно-пропускные пункты таким
образом, чтобы проехать из A в B, минуя
все эти КПП, было бы невозможно. Стоимость
содержания КПП (тыс. долл/год) для каждой
из дорог приведена в таблице.
A
B
C
D
E
F
G
H
I
J
K
L
A
145
90
75
B
135
120
95
C
35
80
150
D
145
35
120
E
135
95
95
F
120
130
80
G
80
130
H
90
45
40
75
I
120
45
115
J
75
40
50
K
95
150
95
80
115
30
L
95
75
50
30
На
каких дорогах следует разместить
контрольно-пропускные пункты, чтобы
минимизировать недовольство
налогоплательщиков штата?
41.
Фирме Red Ass для организации постоянной
связи между городами A и L необходимо
арендовать каналы на телефонных линиях,
соединяющих эти города, а также города
B...K. Стоимость аренды для каждой линии
приведена в таблице.
A
B
C
D
E
F
G
H
I
J
K
L
A
-
30
35
25
B
-
52
72
37
C
30
52
-
24
D
-
52
80
42
30
E
52
-
60
48
75
F
72
60
-
56
G
80
-
26
68
57
H
35
37
24
42
48
-
I
25
30
-
39
J
75
26
-
39
K
68
39
-
L
56
57
39
В
целях обеспечения надежной связи фирма
желает иметь два маршрута для связи,
не имеющих общих линий. На каких линиях
следует арендовать каналы?
42.
Промышленная компания планирует
производство кондиционеров, состоящих
из трех основных частей: корпуса,
вентилятора и мотора. Затраты на
оборудование предприятия станками,
производящими корпуса, вентиляторы и
моторы, равны 20000, 50000 и 80000 $ соответственно.
Однако, если вначале наладить выпуск
вентиляторов, то затраты на остальное
оборудование будут уменьшены на 5 %.
Если вначале пустить в производство
моторы, то затраты на оснащение
предприятия станками двух других типов
уменьшатся на 10 %. Если же в первую
очередь выпускать корпуса, то остальные
затраты уменьшатся на 5 %. После того, как
будет налажен выпуск двух компонентов,
затраты на производство третьего
компонента дополнительно уменьшатся
на 5 %. Определить оптимальную стратегию
изготовления изделий.
43.
Фирма Alamo получила заказ на кирпич,
производимый на ее заводе. Заказ должен
быть выполнен в ближайшие 24 часа, а
время на выполнение одного рейса до
заказчика и обратно составляет 8 часов.
Фирма располагает четырьмя грузовиками,
но имеет возможность арендовать у фирмы
Gilder Rent-A-Truck еще три грузовика.
Грузоподъемность (в т.) и эксплуатационные
расходы (за один рейс) для каждого
грузовика указаны в таблице.
Alamo Gilder 1 2 3 4 1 2 3 Грузоподъемность 15 12 13 16 7 8 6 Экспл.
расходы 25 31 22 30 44 48 41
Всего было заказано
200 т. кирпича. Определить схему перевозки,
имеющую минимальную стоимость.
Лекции
по теории графов./Емеличев В.А., Мельников
О.И., Сарванов В.И., Тышкевич Р.И. – М:
Наука, Гл. ред. физ.-мат. лит., 1990, - 384 с. Майника
Э. Алгоритмы оптимизации на сетях и
графах. – М:Мир, 1981. Филлипс
Д., Гарсиа-Диас А. Методы анализа сетей.
– М: Мир, 1981.
Введние……………………………………………….……..………3 Элементы
теории графов……………………………….…….4 Основные
понятия теории графов……………...…………….4 Способы
задания графов………………………………………10 Связность
графов…………………………………………13 Изоморфизм
графов………………………………………19 Планарные
графы…………………………………………20 Эйлеровы
графы…………………………………….…….21 Гамильтоновы
графы………………………………….….23 Деревья……………………………………………….……24
Контрольные
вопросы к разделу……………………………..28 Задачи
и алгоритмы………………………………………28 Алгоритмы
поиска………………………………………..28 Раскраска
в графах………………………………………..31 Алгоритмы
построения деревьев………………………..35 Алгоритмы
поиска путей…………………………….…..40 Алгоритм
Дийкстры……………………………..…..41 Алгоритм
Форда………………………….……….….42 Алгоритм
Флойда……………………………….……47 Потоковые
алгоритмы……………………………………49 Определения
и постановки задач……………………49 Алгоритм
поиска максимального потока……………55 Алгоритм
поиска потока минимальной стоимости...60 Динамический
поток……………………………….…65 Алгоритм
дефекта…………………………………....68 Контрольные
вопросы к разделу……………………………77 Задачи
для самостоятельного решения……………………..78 Литература…………………………………………………….99
Министерство образования Российской Федерации
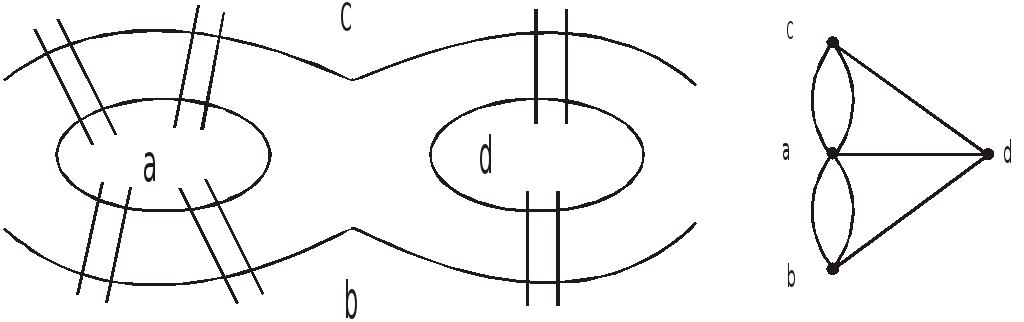
1. Элементы теории графов.
1.1. Основные понятия теории графов
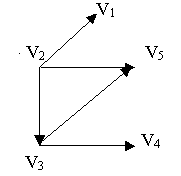
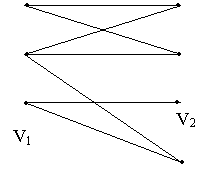
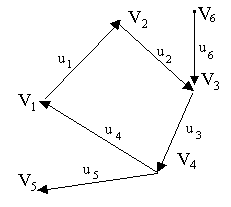
![]() Диаметром
графа называется максимальное из всех
расстояний между вершинами на графе.
Диаметром
графа называется максимальное из всех
расстояний между вершинами на графе.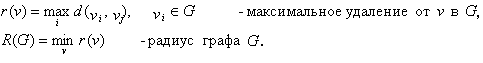
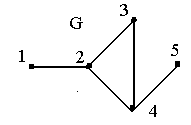 Рис
1.4
Рис
1.4
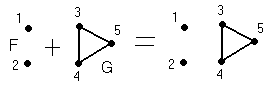
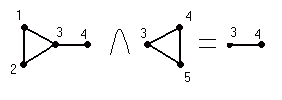
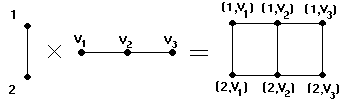
1.2. Способы задания графов
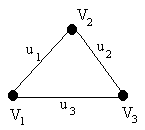
 Матрица
инцидентностиI(G)размерностьюNRсостоит из нулей и единиц и определяет
инцидентность вершин и рёбер графа.
Элементы матрицыI(G)для неографа определяются так:
Матрица
инцидентностиI(G)размерностьюNRсостоит из нулей и единиц и определяет
инцидентность вершин и рёбер графа.
Элементы матрицыI(G)для неографа определяются так: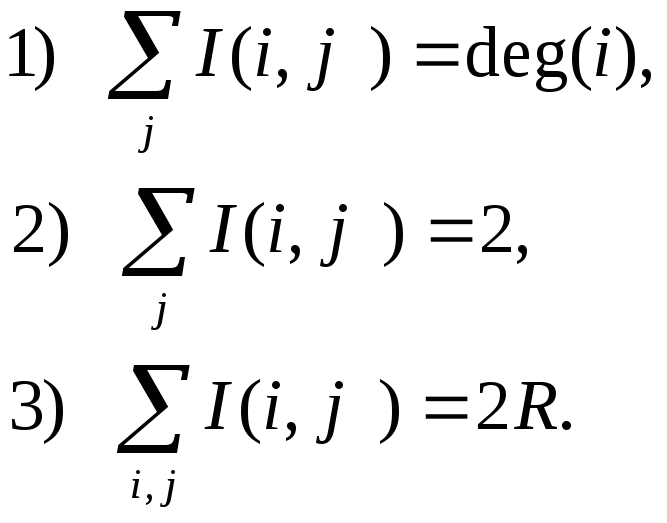
 Матрица
смежностиS(G)имеет размерностьNNи определяет отношение между вершинами
графа. Элементы матрицыSопределяются так:
Матрица
смежностиS(G)имеет размерностьNNи определяет отношение между вершинами
графа. Элементы матрицыSопределяются так: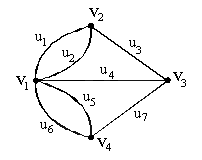
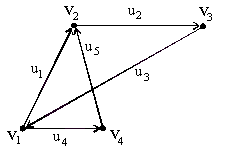
1.3. Связность графов
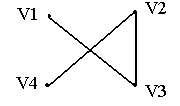
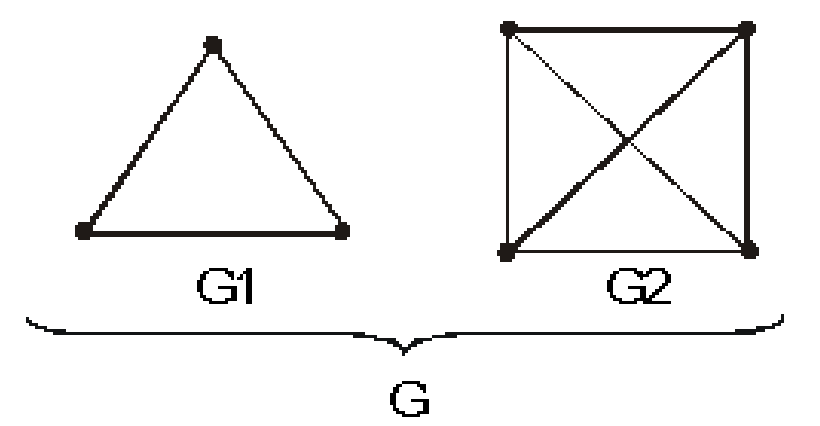
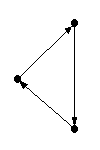
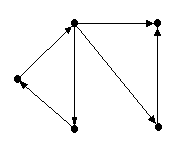
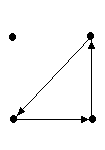

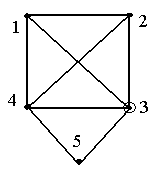
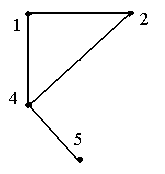
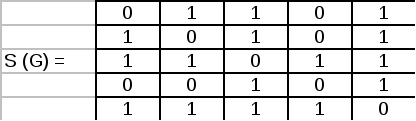

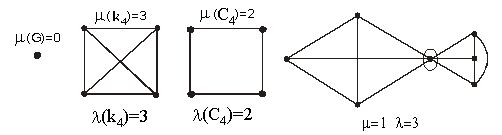
 k4
k4
 C4
C4
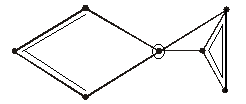
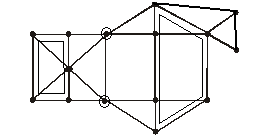 Рис
1.24
Рис
1.24
1.4. Изоморфизм графов
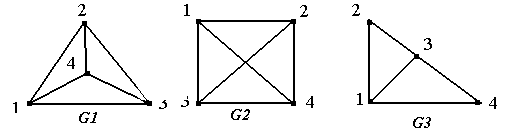
1.5. Планарные графы
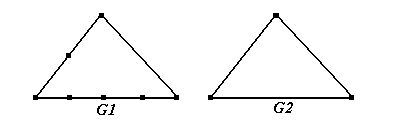
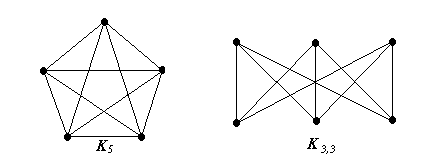
1.6. Эйлеровы графы
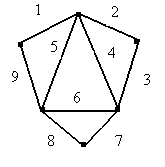
1.7. Гамильтоновы графы
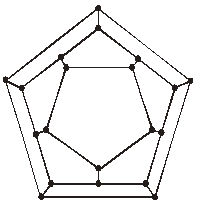
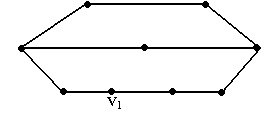
1.8. Деревья
![]()
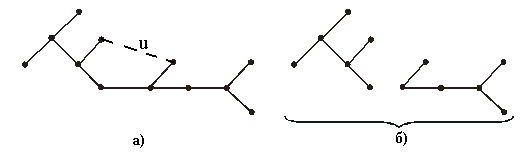
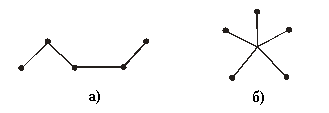
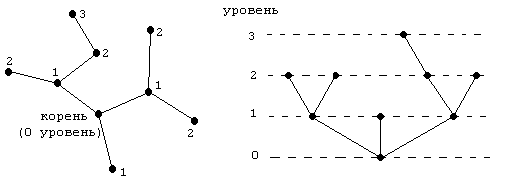
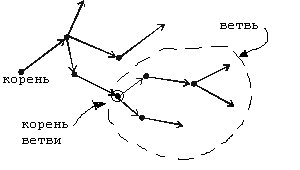
Контрольные вопросы
2. Задачи и алгоритмы
2.1. Алгоритмы поиска
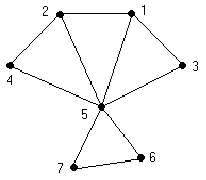
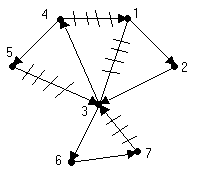
2.2. Раскраска в графах
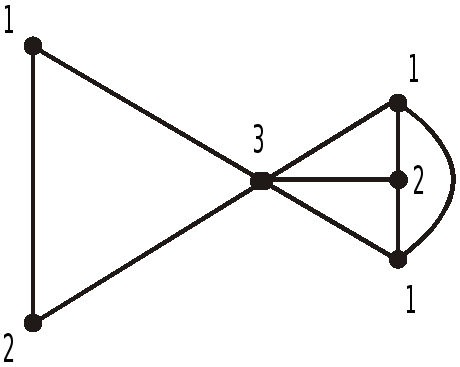
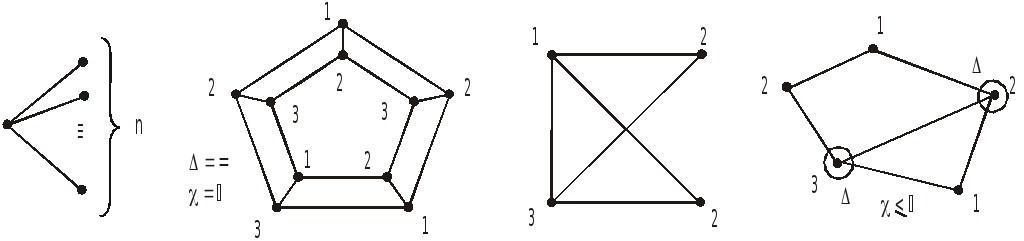
2.3. Алгоритмы построения деревьев
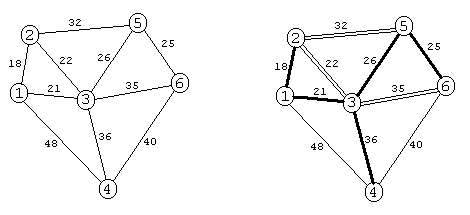
2.4. Алгоритмы поиска путей
2.4.1. Алгоритм Дийкстры
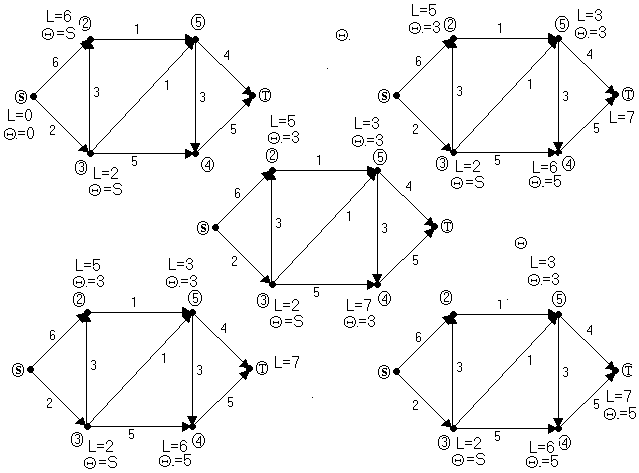
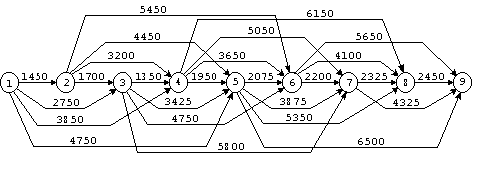
![]() Длина
дугиaij(в данном случае – стоимость) вычисляется
по формуле гдеPi– стоимость автомобиля в началеi-го
года,mk– эксплуатационные расходы в течениеk-го года,Sj– ликвидационная стоимость автомобиля
в началеj-го года.
Оптимальному решению соответствует
кратчайший путь из вершины 1 в вершину
9. В таблице приведены результаты
вычислений по алгоритму Дийкстры метокd(i).
Просмотренные узлы выделены.
Длина
дугиaij(в данном случае – стоимость) вычисляется
по формуле гдеPi– стоимость автомобиля в началеi-го
года,mk– эксплуатационные расходы в течениеk-го года,Sj– ликвидационная стоимость автомобиля
в началеj-го года.
Оптимальному решению соответствует
кратчайший путь из вершины 1 в вершину
9. В таблице приведены результаты
вычислений по алгоритму Дийкстры метокd(i).
Просмотренные узлы выделены.
2.4.2. Алгоритм Форда
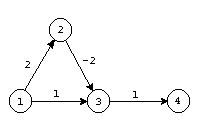
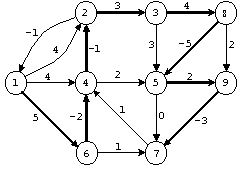
2.4.3. Алгоритм Флойда

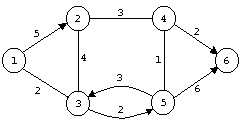
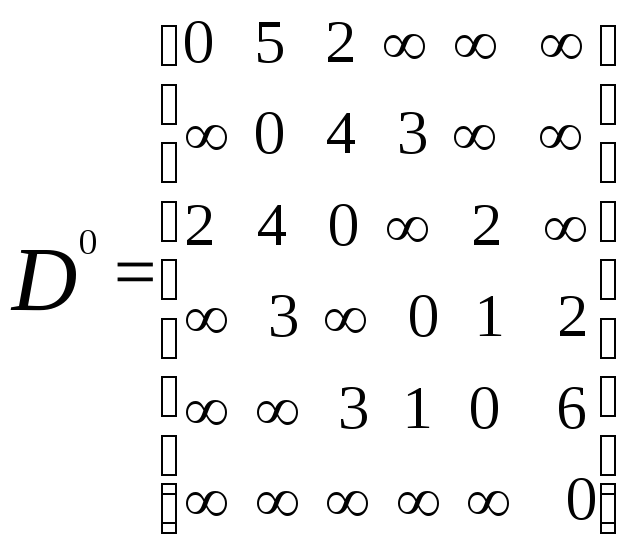
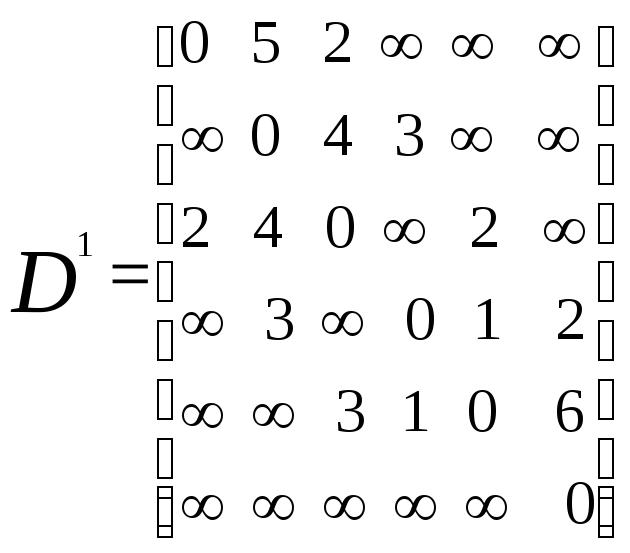
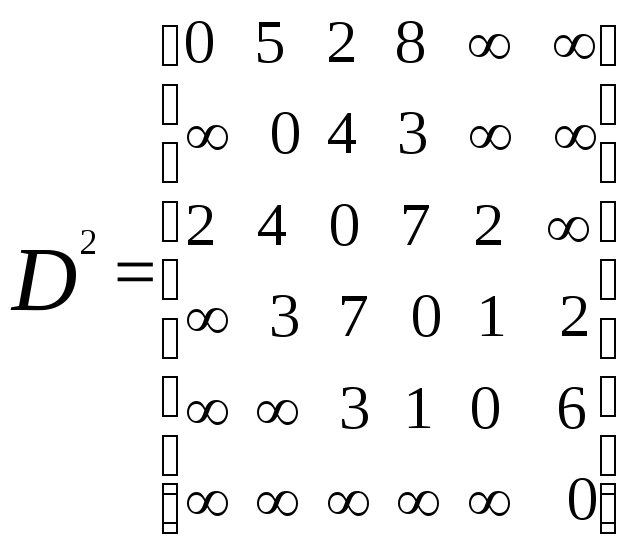
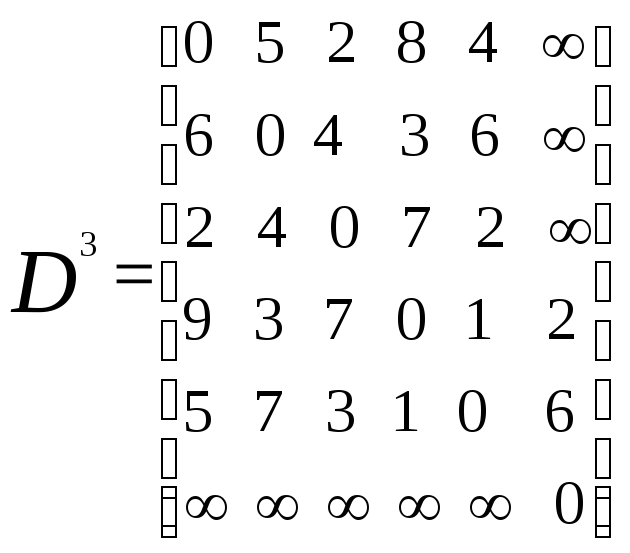
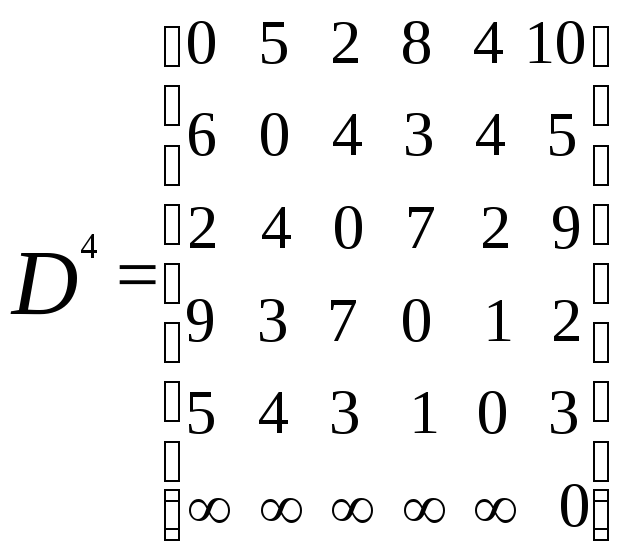
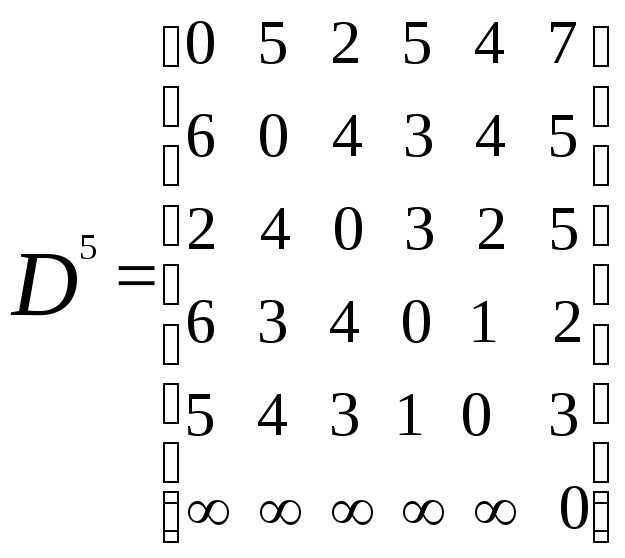
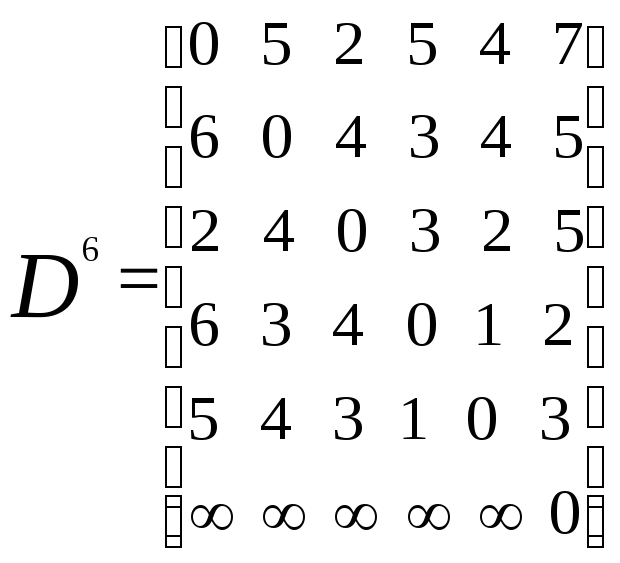
2.5. Потоковые алгоритмы
2.5.1. Определения и постановки задач
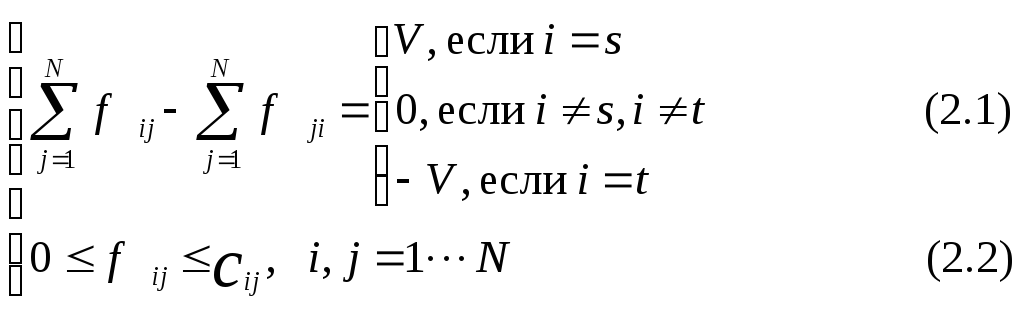
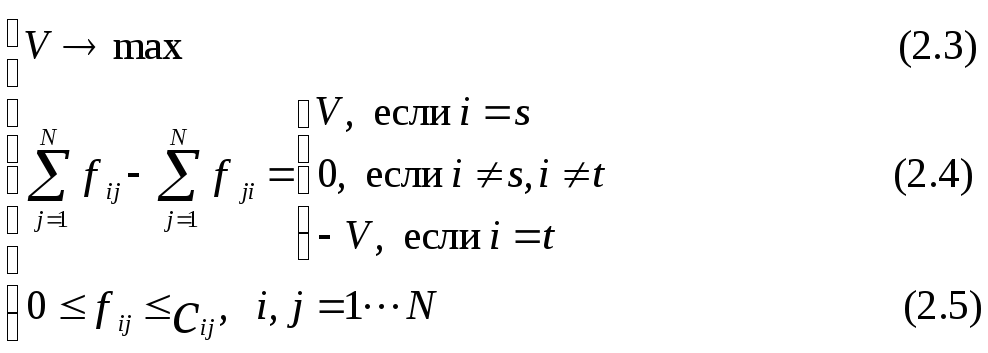
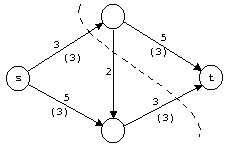

![]()
![]()
![]()
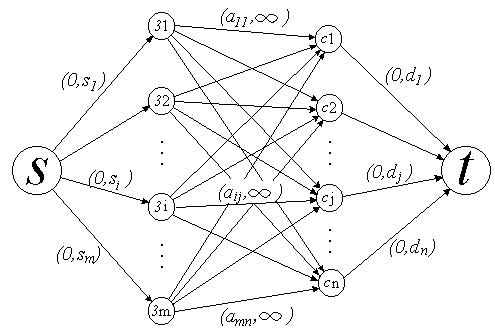
2.5.2. Алгоритм поиска максимального потока
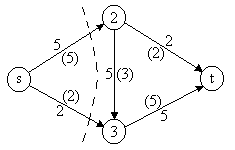
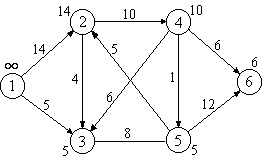
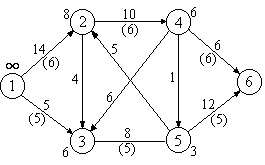
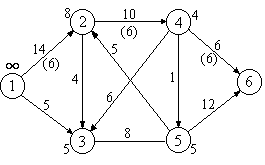
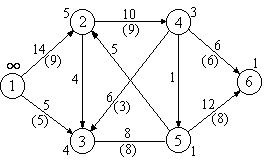
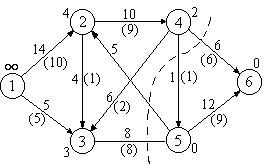
2.5.3. Алгоритм поиска потока минимальной стоимости
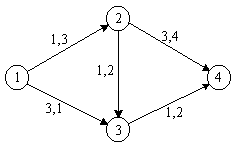
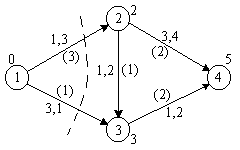
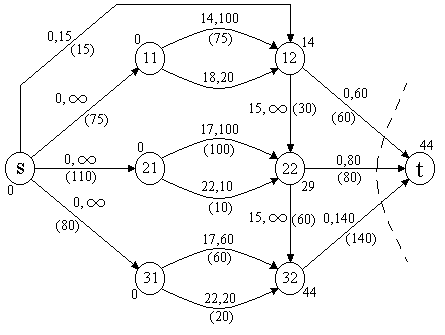
2.5.4. Динамический поток
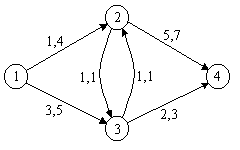
2.5.5. Алгоритм дефекта

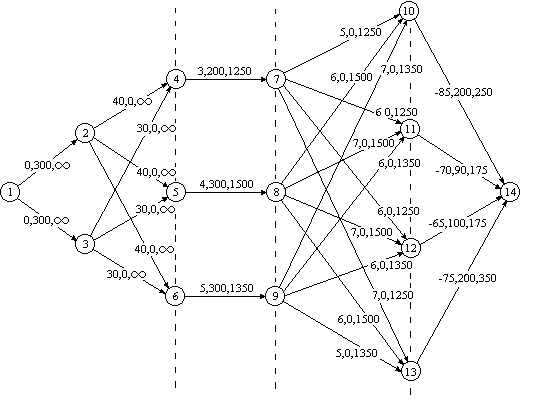
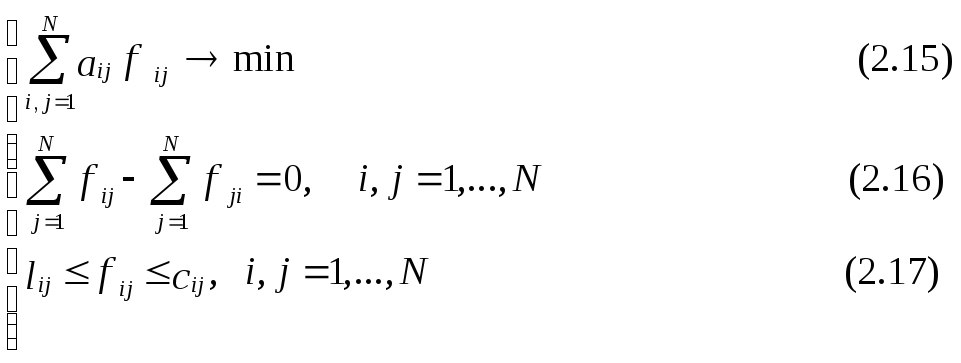
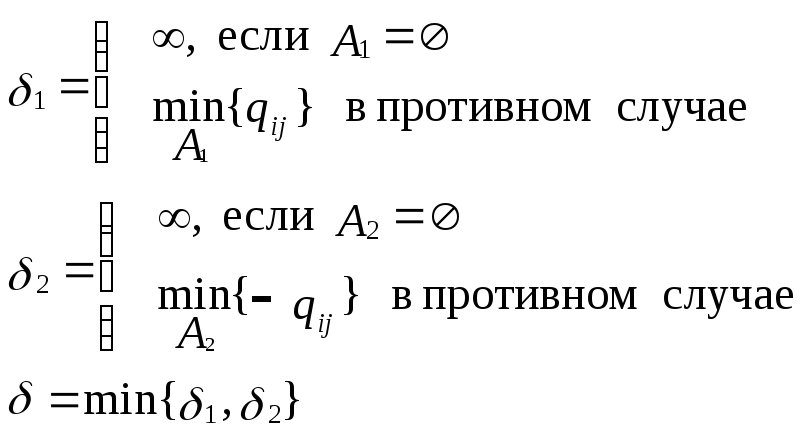
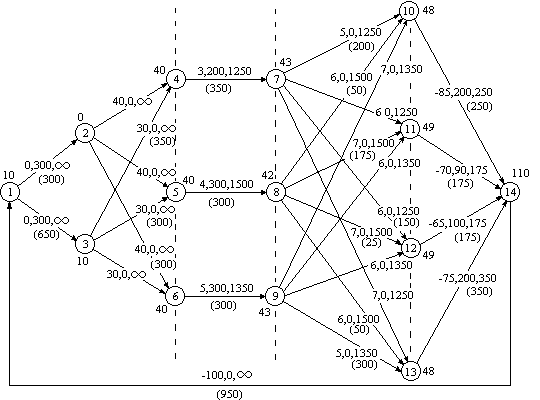
Контрольные вопросы
3. Задачи для самостоятельного решения
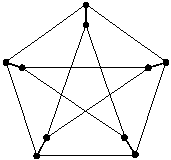

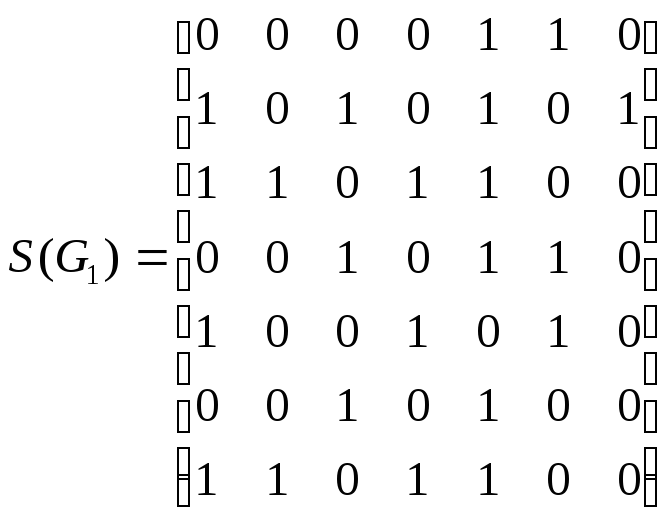
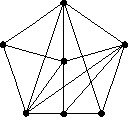
![]() .
.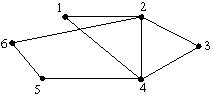
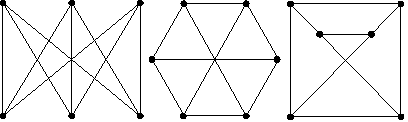
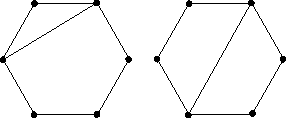
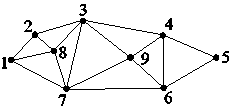
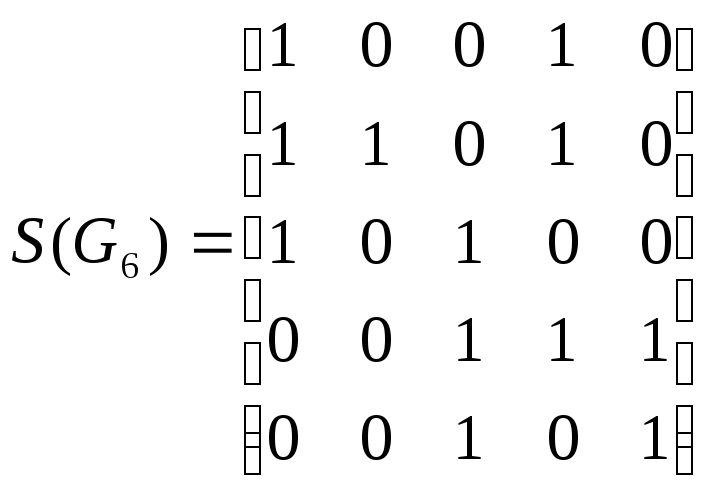
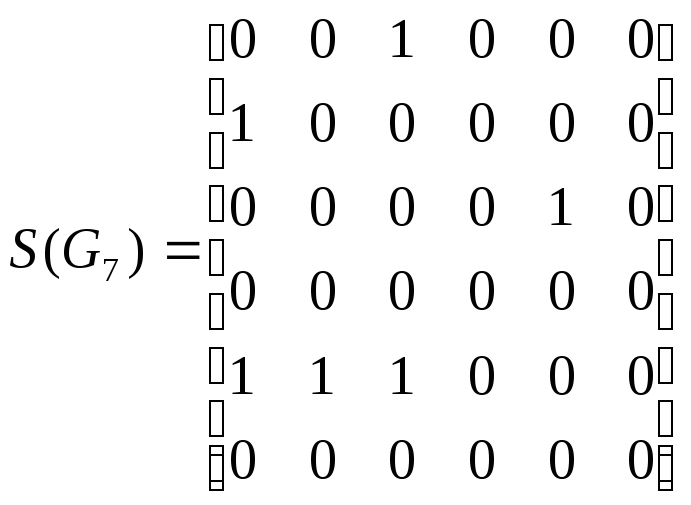
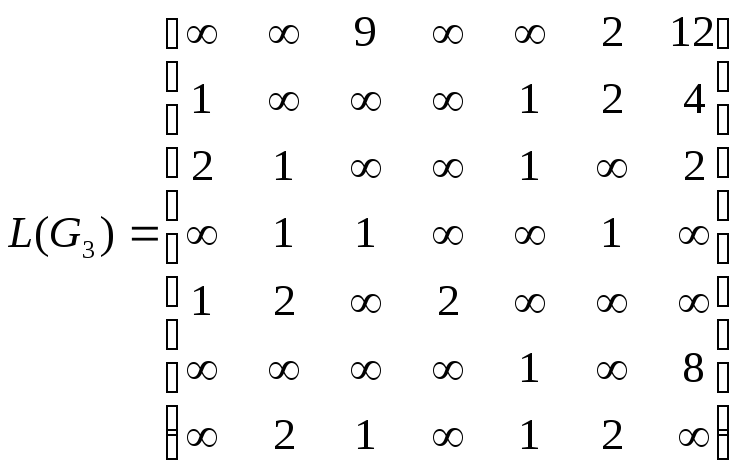
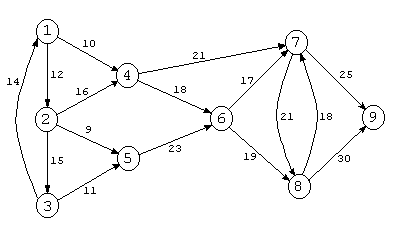
4. Литература
Содержание
3
4
5
6
7
8
9 100
10 99
11 98
12 97
13 96
14 95
15 94
16 93
17 92
18 91
19 90
20 89
21 88
22 87
23 86
24 85
25 84
26 83
27 82
28 81
29 80
30 79
31 78
32 77
33 76
34 75
35 74
36 73
37 72
38 71
39 70
40 69
41 68
42 67
43 66
44 65
45 64
46 63
47 62
48 61
49 60
50 59
51 58
52 57
53 56
54 55
