3. Діаграма критичних напружень
З
формули для критичних напружень (8)
видно, що в залежності від гнучкості
,
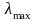критичне напруження
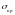може бути різним. Якщо гнучкість
порівняно невелика, то
може набувати значень, що перевищують
границю пропорційності матеріалу
стрижня
.
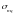Оскільки формула Ейлера і формула для
визначення
одержані за допущення, що стрижень під
час втраті стійкості деформується
пружно і матеріал знаходиться в межах
закону Гука (тобто
),
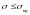то величина критичних напружень повинна
бути обмежена
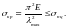
Звідки
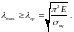(9)
Тобто,
нижня
границя гнучкості
стрижня, за якої можна застосовувати
формулу Ейлера, становить
.
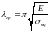Так, для сталі Ст. 3 з пружними
характеристиками
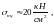
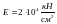дістаємо
.
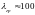Отже, для таких сталей формула Ейлера
застосовна, якщо
.
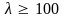Це – область
стрижнів великої гнучкості.
Область гнучкостей
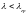можна розділити на:
а) область
малих гнучкостей (для
сталі Ст. 3
),
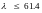за яких немає небезпеки
втрати стійкості і
стрижні слід перевіряти тільки на
міцність. Якщо
напруження
,
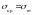де
- границя текучості матеріалу стрижня;
б) область
середніх гнучкостей
(для сталі Ст. 3
).
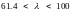Визначення критичних напружень в цій
області викликає певні труднощі, оскільки
матеріал в цьому випадку перебуває в
пружнопластичному стані (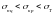
).
У інженерних розрахунках для визначення
цих напружень застосовують формулу
Ясинського, що одержана за результатами
обробки експериментальних даних:
(10)
де
коефіцієнти
,
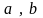беруться з таблиць. Зокрема, для сталі
Ст. 3
.
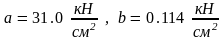Для дерева (сосна)
.
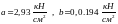Для
кожного матеріалу за різних значеннях
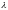можна на основі наведених вище
співвідношень побудувати графік
залежності напруження
від гнучкості
.
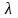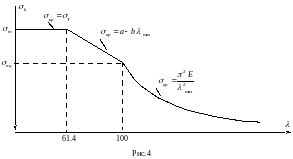
Цей графік називається діаграмою
критичних напружень.
Для сталі Ст. 3 ця діаграма показана на
рис. 4.
Умова стійкості центрально стиснутого стрижня має вигляд
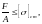(11)
де
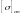- допустиме
напруження стійкості.
Це напруження виражають через основне
допустиме напруження на стиск
:
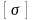(12)
4. Проектний розрахунок стиснутих стрижнів на стійкість
де
- коефіцієнт
поздовжнього згину
(зменшення основного допустимого
напруження стиску) (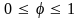
),
що залежить від матеріалу та гнучкості
стрижня. Значення цього коефіцієнта
беруться з таблиці.
З урахуванням виразу (12) умова стійкості (11) набуває вигляду
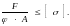(13)
Виходячи з умови стійкості, можна розв’язувати наступні типи задач:
а) перевіряти стійкість заданого стрижня, формула (13);
б) Визначати допустиму стискальну силу за формулою
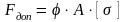; (14)
в) добирати необхідні розміри поперечних перерізів стиснутих стрижнів за формулою
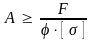. (15)
Під
час розв’язуванні задач останнього
типу використовують метод послідовних
наближень, оскільки у формулі (15) є дві
невідомі – шукана площа поперечного
перерізу
,
та коефіцієнт
.
(Коефіцієнт
знаходиться із таблиць в залежності
від
.
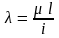Якщо розміри поперечного перерізу
невідомі, то невідомі і радіуси інерції
перерізу “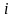
“,
а отже відповідно і гнучкість
та коефіцієнт
).
З
питанням добору розмірів поперечного
перерізу центрально стиснутого стрижня
тісно пов’язане питання раціональної
форми поперечних перерізів. Небезпека
втрати стійкості стиснутого стрижня
тим менша, чим менша його найбільша
гнучкість
,
тобто чим більші, за фіксованого значення
площі поперечного перерізу
,
головні радіуси інерції “
“
поперечного перерізу. Матеріал у таких
перерізах повинен бути розміщений
якомога далі від центра перерізу. Цим
вимогам найкраще відповідають порожнисті
всередині перерізи з можливо тонкою
стінкою. При цьому також слід прагнути
задовольнити умову рівностійкості (7).
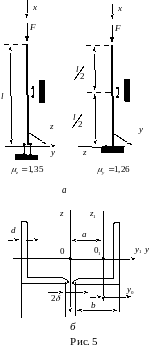
Приклад
1.
Підібрати за сортаментом прокатної
сталі і раціонально розмістити поперечний
переріз стояка завдовжки
,
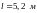який складається з двох нерівнобоких
кутників і стискається осьовою силою
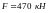(рис. 5,
а).
Матеріал, з якого виготовлені кутники
– сталь з допустимим напруженням на
стиск
.
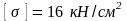Схема закріплення стояка показана на
рис. 6, а.
Розмір
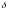прийняти рівним товщині полички
.
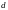Встановлюємо
коефіцієнти зведеної довжини для обох
головних площин: при згині відносно осі
(у площині
)
;
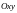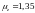при згині відносно осі
(у площина
)
.
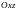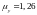Оскільки
,
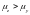переріз необхідно розмістити так, щоб
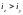(рис.
5,
б).
У цьому разі значення критичної сили
буде найбільшим.
Гнучкості стрижня виражаємо через невідомі поки що головні радіуси інерції :
у
площині
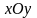( відносно осі
)
;
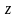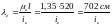у
площині
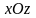( відносно осі
)
.
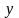Потрібні розміри поперечного перерізу одного кутника підбираємо з умови стійкості (15) методом послідовних наближень.
I
наближення:
Прийнявши
,
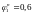маємо:
.
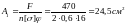Рис.
6 Тут
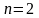- кількість кутників.
З
таблиці сортаменту (ГОСТ 8510 - 72) (дод. 1)
добираємо кутник
,
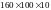для якого
,
,
,
,
,
.
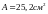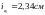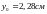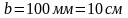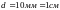Визначимо головні радіуси інерції перерізу стояка:
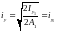=5,13см;
;
,
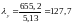де
а – відстань
між осями
і
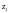(рис. 6, б).
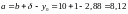см,
,
.
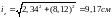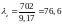Оскільки
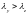підбір перерізу будемо здійснювати за
гнучкістю у площині
,
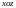тобто
.
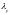З
таблиці коефіцієнтів
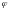(табл. 1 дод. 2) для сталі Ст.3 маємо:
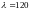
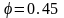для
,
для
.
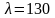
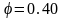Методом
лінійної інтерполяції для
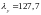знаходимо:
.
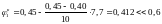II
наближення:
візьмемо значення коефіцієнту
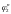як середнє арифметичне початкового і
кінцевого значень першого наближення
.
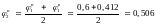Обчислюємо потрібну площу одного кутника
.
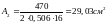За
таблицями сортаменту вибираємо кутник
,
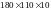для якого
,
,
,
.
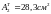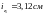
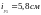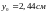Максимальна гнучкість стрижня
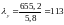і
,
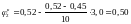що є близьке до значення
з точністю до двох знаків після коми.
Різниця
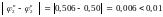Обчислення припиняємо.
Розміри поперечного перерізу, прийняті в другому наближенні є близькі до оптимальних. Виконуємо перевірку за напруженнями:
.
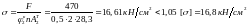.Допускається перевантаження 5%.
Перевіряємо
стійкість стояка в площині
,
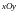за
.
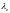Маємо:
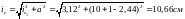і
.
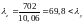Стійкість в площині також забезпечена.
Перевіряємо
коефіцієнт запасу стійкості стояка з
вибраними розмірами поперечного
перерізу. Оскільки
,
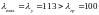то до стояка можна застосувати формулу
Ейлера.
За формулою (8) знаходимо:
.
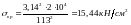Критична сила
;
.
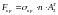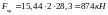Згідно з формулою (1) коефіцієнт запасу стійкості:
.
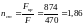СПИСОК ЛІТЕРАТУРИ
1. Беляев Н. М. Сопротивление материалов. – М.: Физматгиз, 1962.
2. Сборник задач по сопротивлению материалов / Под ред. В. К. Качурина. – М.: Наука, 1970.
3. Ковтун В. В., Павлов В. С., Дорофеєв О. А. Опір матеріалів Розрахункові роботи. – Львів: Афіша, 2002.
4. Корнілов О. А. Опір матеріалів. – К.: ЛОГОС, 2000.
5. Сопротивление материалов / Под. ред. Н. А. Костенко. – М.: Высшая школа, 2000.
6. Писаренко Г. С., Квітка О. Л., Уманський Е. С. Опір матеріалів. – К.: Вища школа, 1993.
7. Посацький С. Л. Опір матеріалів. – Львів, 1973.
НАВЧАЛЬНЕ ВИДАННЯ
КУРСОВА РОБОТА
ЗАВДАННЯ ТА МЕТОДИЧНІ ВКАЗІВКИ
з курсу “Опір матеріалів” для студентів базового напряму