1. Вычисление определенных интегралов Справочная информация

При решении инженерных задач возникают ситуации, когда аналитическое вычисление определённого интеграла затруднено или невозможно. В подобных ситуациях решение может быть получено одним из методов приближенного вычисления значения определённого интеграла.

В се методы приближенного вычисления определённых интегралов основаны на геометрическом смысле интеграла Ньютона-Лейбница. Он заключается в том, что определенный интеграл

численно равен площади S криволинейной трапеции, ограничен­ной графиком подынтегральной функции f(x) и осью абсцисс на отрезке [a, b] (см. рис.1).

П

Рис.1.

оэтому для приближённого вычисления определённого интеграла доста­точно подсчитать площадь трапеции S. Можно указать множество способов вычисления площади S. Простейшие из них – формулы прямоугольников, трапеций и Симпсона.

Формула средних прямоугольников

В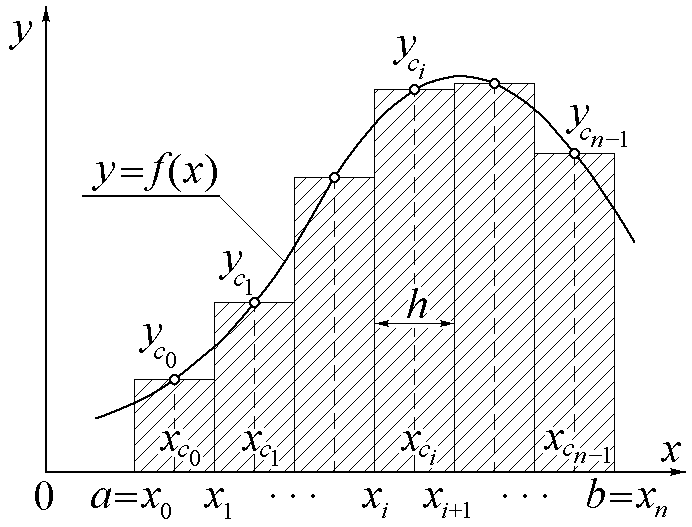 формуле средних прямоугольников криволинейная трапеция представляется набором прямоугольников (см. рис.2). В этом случае площадь криволинейной трапеции представляется в виде суммы площадей этих прямоугольников, а интеграл I приближенно вычисляется по формуле

Рис.2.

или в развёрнутом виде

,

где – абсцисса центральной точки i-го участка разбиения отрезка [a, b], h = (b – a)/n – шаг равномерного разбиения отрезка, n – количество участков разбиения.

Формула трапеций

А налогично вычисляется определённый интеграл по формуле трапеций, где площадь криволинейной трапеции S заменяется суммой площадей элементарных трапеций (см. рис.3). Такой подход приводит к вычислению определённого интеграла I по формуле

Рис.3.

или, раскрывая сумму,

.

Формула Симпсона (J.Gregory(Грегори) 1668, Th.Simpson 1743)

В

Рис.4.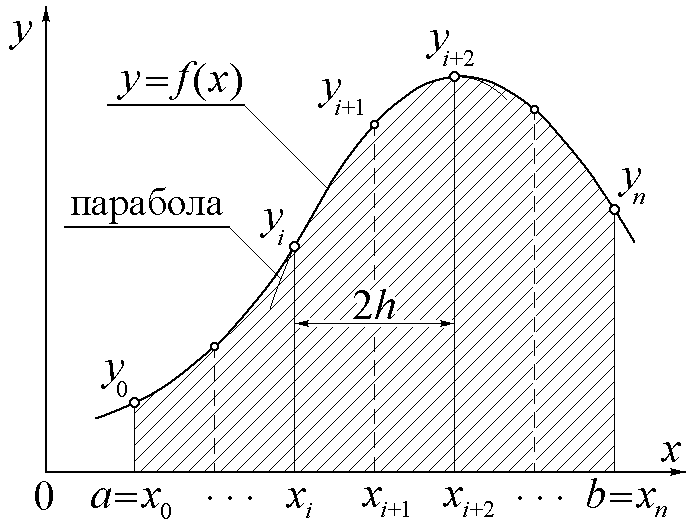

формуле Симпсона площадь криволинейной трапеции рассчитывается как сумма площадей ряда криволинейных трапеций, у которых криволинейная сторона представляет собой участок параболы, проходящей через три соседние точки на графике подынтегральной функции. Это можно видеть на рис.4. Поэтому число участков разбиения отрезка [a,b] в отличие от предыдущих способов обязательно должно быть чётным. Исходя из этого, значение определённого интеграла приближённо вычисляется по формуле

.

Реализация формул

Основой реализации любого вычислительного метода в программе Excel является представление его алгоритма в виде таблицы. При этом часто используется следующий подход: столбцами таблицы являются последовательно получаемые промежуточные результаты расчёта при одном значении аргумента или на одной итерации, а строками – последовательность значений аргумента или итерации. Иногда из этой закономерности выпадает первая строка таблицы, так как её используют для ввода начальных значений.

Описанный выше подход к формированию расчётной таблицы не является догмой. Каждый пользователь вправе использовать свой подход, но обычно он в той или иной мере основывается на описанных выше принципах.

Пример. Вычислить в программе Excel интеграл

с шагом интегрирования h = 0.1.

Для вычисления значения интеграла можно воспользоваться формулой средних прямоугольников. Одна из возможных её реализаций представлена таблицей 1 следующего вида (см. формулу)

Таблица 1.

i	xi
0	x0
1	x1
…	….	………	………
n–1	xn–1

Столбец «i» не несет никакой информационной нагрузки, кроме пояснения к используемым формулам, а потому при реализации в программе Excel может быть опущен. Таблица интегрирования будет выглядеть следующим образом (см. рис.5)

Рис.5.

Результат интегрирования располагается в ячейке С12, где он вычисляется с помощью встроенной функции СУММ:

= 0,1*СУММ(С2:С11).

Аналогичным образом может быть построена таблица вычисления заданного интеграла по формуле трапеций (см. ниже рис.6)

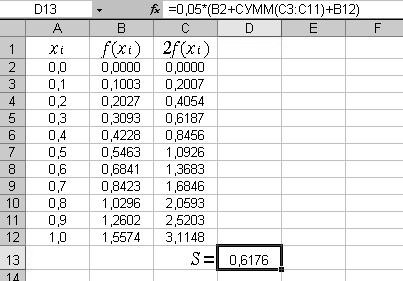
Рис.6.

Так как в формуле трапеций все значения функции (кроме двух крайних) удваиваются, то в таблицу удобно ввести столбец С. При таком подходе интеграл в ячейке D13 тоже удобно вычислять с помощью функции СУММ.

Выбор ячейки D13 для записи результата может быть произвольным и делается только из соображений эстетики.

Доработав приведённую выше таблицу легко вычислить интеграл по формуле Симпсона (см. рис.7). Здесь так же используются дополнительные столбцы для записи отдельных групп слагаемых.

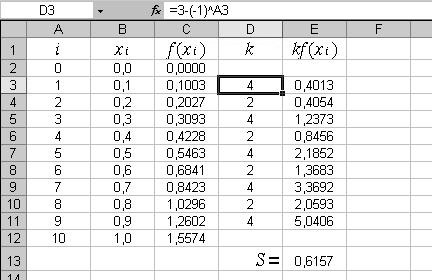
Рис.7.

Результат интегрирования располагается в ячейке E13.

Оценка погрешностей численных способов интегрирования

Точность вычисления любой величины определяется погрешностью, которая может быть представлена в абсолютной или относительной форме. Абсолютная погрешность величины есть модуль разницы между её точным и приближённым значениями. Например, между точным значением определённого интеграла и его значением, полученным выбранным численным способом при конкретном количестве участков разбиения отрезка [a, b]

.

Относительная погрешность является более информативным параметром точности вычисления искомой величины. Она оценивает ошибку решения в долях точного (или лучшего из имеющихся) значения этой величины и вычисляется как модуль отношения разницы между точным и вычисленным значениями величины к её точному значению

.

Анализ формул численного интегрирования непрерывно диф­­ференциру­емых на отрезке [a, b] подынтегральных функций f(x) позволяет получить следующие оценки абсолютных погрешностей вычисления интегралов:

• для формулы средних прямоугольников ;

• для формулы трапеций ;

• для формулы Симпсона .

На практике, такое вычисление погрешностей при интегрировании затруднено, так как требует решения дополнительной, зачастую даже более сложной, задачи поиска максимума высших производных подынтегральной функции. Поэтому чаще для вычисления погрешности методов используют апостериорные оценки, базирующиеся на правиле Рунге (правило двойного счёта). В основу этого подхода к оценке погрешности методов интегрирования положено утверждение, заключающееся в том, что все формулы для погрешностей имеют одну и ту же структуру

,

где коэффициент C_m включает в себя длину участка интегрирования, максимум модуля производной и соответствующий коэффициент, а степень m определяется видом используемой формулы численного интегрирования (m = 2 для формул средних прямоугольников и трапеций и m = 4 для формулы Симпсона). Использование этой зависимости при уменьшении шага интегрирования вдвое позволяет записать погрешность вычисления интеграла в виде

.

Сравнение последних двух формул даёт основное соотношение правила Рунге, справедливое для всех способов приближённого вычисления интеграла

,

где S(h/2) и S(h) – приближённые значения интеграла, вычисленные при шагах разбиения отрезка [a, b], отличающихся друг от друга в два

раза. Исходя из этого, для оценки погрешности вычисленного значения интеграла с выбранным шагом надо повторить вычисления, удвоив величину шага, и воспользоваться приведённым выше соотношением.

Например, если требуется вычислить рассмотренный выше интеграл с относительной погрешностью, не превышающей 0.5%, то для выполнения задания можно воспользоваться формулой средних прямоугольников, выбрав в качестве первоначального значения шага интегрирования h = 0.5, т.е. разбив отрезок [0, 1] на два участка с граничными точками 0, 0.5 и 1.0. Тогда приближённое значение интеграла будет S(0.5) = 0.5935. При уменьшении шага интегрирования вдвое (h = 0.25), т.е. при разбиении отрезка интегрирования на 4 участка, значение интеграла будет равно S(0.25) = 0.6095. Таким образом, абсолютная и относительная погрешности вычисления последнего значения интеграла могут быть вычислены по правилу Рунге

,

.

В связи с тем, что требуемая точность вычисления интеграла не достигнута, решение продолжается: шаг интегрирования уменьшается ещё в два раза (h = 0.125). В этом случае значение интеграла будет равно 0.6141, а его абсолютная и относительная погрешности составят 0.0046 и 0.75%, соответственно. Видно, что требуемая точность опять не достигнута, поэтому шаг интегрирования уменьшается ещё в два раза (h = 0.0625) и вычисления повторяются. С таким шагом значение интеграла получается равным 0.6152, его абсолютная погрешность – 0.0011, а относительная – 0.18%. Таким образом, при шаге интегрирования h = 0.0625 решение задачи, равное 0.6152, получено с заданной погрешностью.

Если постановка задачи требует получение результатов с меньшей погрешностью, чем была получена, то необходимо дальнейшее уменьшение величины шага разбиения отрезка интегрирования [a, b]. Однако этот процесс нельзя продолжать бесконечно. Он ограничивается точностью представления данных в ЭВМ: существует некоторое минимальное значение шага разбиения отрезка [a, b], дальнейшее уменьшение которого вызовет рост погрешности вычисления интеграла.