
- •Кафедра «Прикладная и вычислительная математика»
- •Введение
- •1. Вычисление определенных интегралов Справочная информация
- •Формула средних прямоугольников
- •Формула трапеций
- •Контрольные задания
- •2. Решение нелинейных уравнений Справочная информация
- •Контрольные задания
- •3. Решение систем линейных алгебраических уравнений Справочная информация
- •Метод Гаусса с выбором главного элемента
- •Метод простых итераций
- •Программное обеспечение Excel’а
- •Контрольные задания
- •4. Интерполяция таблично заданных функций Справочная информация
- •Кусочно-линейная интерполяция
- •Контрольные задания
- •5. Аппроксимация таблично заданных функций Справочная информация
- •В заключении рассчитывается аппроксимирующая сглаживающая функция и строится её гладкий график, на котором точками отображаются значения исходной табличной функции.
- •Контрольные задания
- •6. Решение задачи коши для обыкновенных дифференциальных уравнений 1-го порядка Справочная информация
- •Усовершенствованный метод Эйлера
- •Оценка погрешностей методов
- •Контрольные задания
- •Список литературы
- •Содержание
Контрольные задания
Найти все лежащие на указанном отрезке корни уравнения с относительной разницей между соседними значениями приближения каждого корня не более чем 0.00001. Для этого реализовать указанный преподавателем метод. Оценить относительную погрешность полученных значений корней.
1.
![]() ,
(0
x
4). 2.
,
(0
x
4). 2.
![]() ,
(2
x
10).
,
(2
x
10).
3.
![]() ,
(0
x
4). 4.
,
(0
x
4). 4.
![]() ,
(0
x
8).
,
(0
x
8).
5.
![]() ,
(3
x
12). 6.
,
(3
x
12). 6.
![]() ,
(0
x
4).
,
(0
x
4).
7.
![]() ,
(0
x
4). 8.
,
(0
x
4). 8.
![]() ,
(0
x
10).
,
(0
x
10).
9.
![]() ,
(0
x
4).
,
(0
x
4).
10.
![]() ,
(0
x
3.5).
,
(0
x
3.5).
11.
![]() ,
(0
x
4).
,
(0
x
4).
12.
![]() ,
(0
x
4). 13.
,
(0
x
4). 13.
![]() ,
(0
x
8).
,
(0
x
8).
14.
![]() ,
(0
x
2).
,
(0
x
2).
15.
![]() ,
(0
x
4).
,
(0
x
4).
16.
![]() ,
(0
x
8).
,
(0
x
8).
17.
![]() ,
(1
x
6).
,
(1
x
6).
18.
![]() ,
(0
x
8).
,
(0
x
8).
19.
![]() ,
(0
x
2).
,
(0
x
2).
20.
![]() ,
(2
x
4).
,
(2
x
4).
21.
![]() ,
(2
x
15).
,
(2
x
15).
22.
![]() ,
(0
x
2). 23.
,
(0
x
2). 23.
![]() ,
(0
x
8).
,
(0
x
8).
24.
![]() ,
(2
x
8).
,
(2
x
8).
25.
![]() ,
(0
x
8).
,
(0
x
8).
26.
![]() ,
(2
x
12).
,
(2
x
12).
27.
![]() ,
(0
x
8).
,
(0
x
8).
28.
![]() ,
(0
x
2,5).
,
(0
x
2,5).
29.
![]() ,
(0
x
3).
,
(0
x
3).
30.
![]() ,
(0
x
6).
,
(0
x
6).
3. Решение систем линейных алгебраических уравнений Справочная информация
Численные методы решения систем линейных алгебраических уравнений
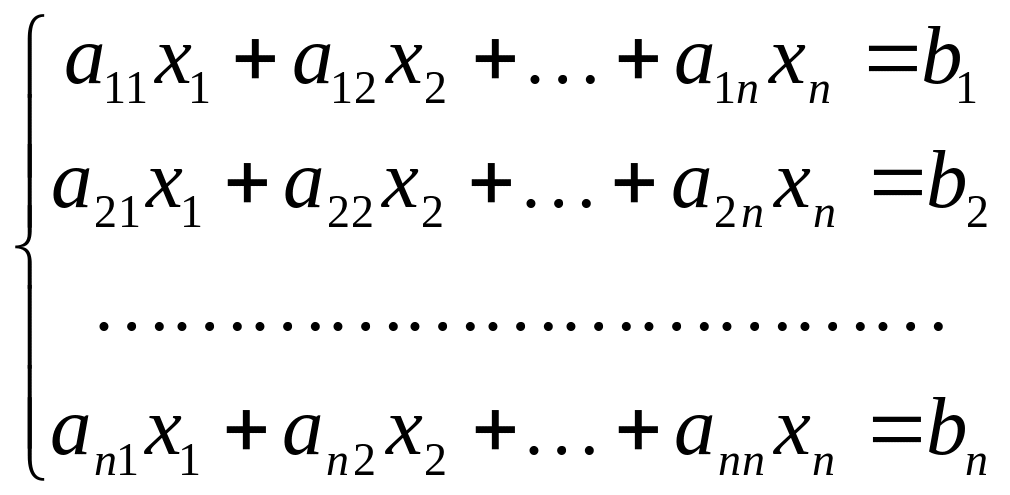 ,
,
записываемых в матричной форме в виде
![]() ,
,
где
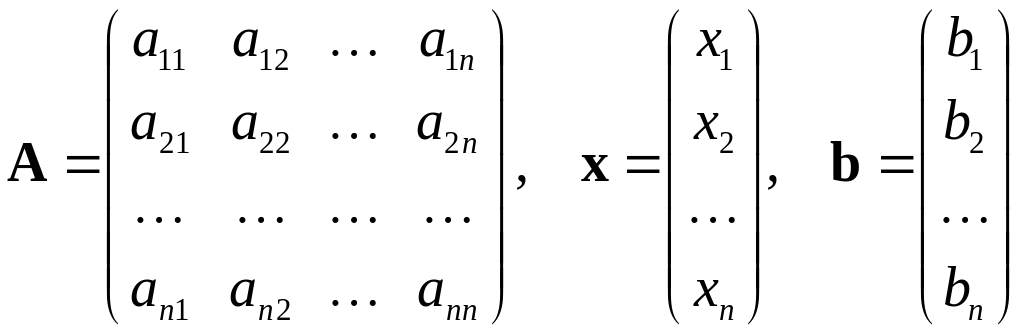 ,
,
делятся на точные и итерационные. Они используются для систем, у которых количество неизвестных равно количеству уравнений и матрица A - не вырождена (её определитель не равен нулю). Точными методами условно называют методы, которые дают решение задачи посредством конечного числа арифметических операций. Итерационные методы позволяют получить решение системы как предел бесконечной последовательности его приближений. При применении итерационных методов существенным вопросом является вопрос об их сходимости.
Точные методы, к которым относятся метод Гаусса и его разновидности, не имеют дополнительных ограничений на свойства матрицы системы.
Метод Гаусса (K.F.Gauβ, 1849)
В основе метода Гаусса лежит идея последовательного исключения неизвестных, приводящая исходную систему с квадратной матрицей к легко разрешимой системе с верхней треугольной матрицей
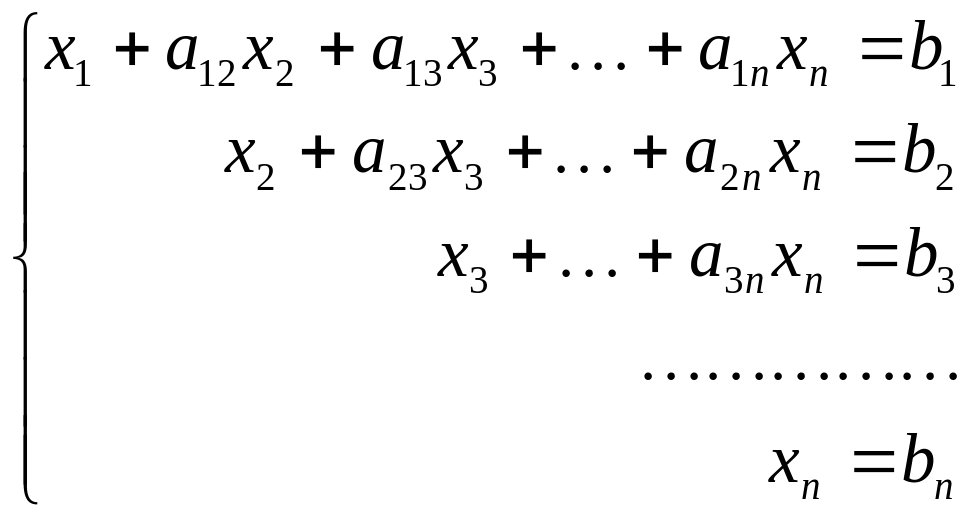 .
.
Данное преобразование может быть осуществлено многими способами. Однако все они основаны на свойстве систем, которое заключается в неизменности их решений при умножении любого уравнения на отличную от нуля постоянную или его замене на сумму с любым другим уравнением.
Один из простейших способов исключения состоит в следующем. Первое уравнение системы
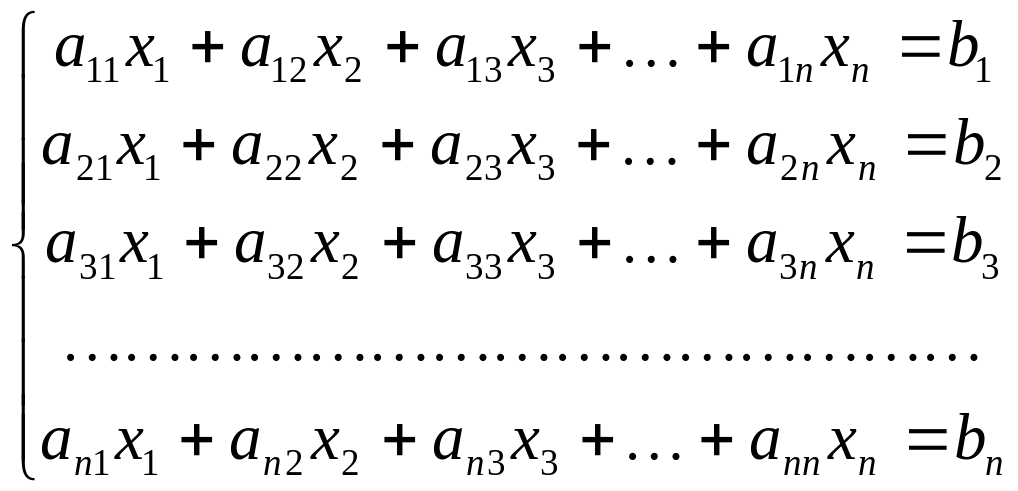 ,
,
которое на этом шаге считается ведущим, нормируется – делится на значение диагонального элемента a11
![]()
или
![]() ,
,
где
![]() .
.
Если в исходной системе a11= 0, то в качестве первого уравнения следует взять любое другое с ненулевым первым коэффициентом, поменяв их местами. Полученное уравнение умножается на первый коэффициент второго уравнения a21 и вычитается из него. В результате во втором уравнении пропадает слагаемое a21x1, содержащее первое неизвестное x1. Такие же операции проводятся со всеми последующими уравнениями. В результате система уравнений принимает вид
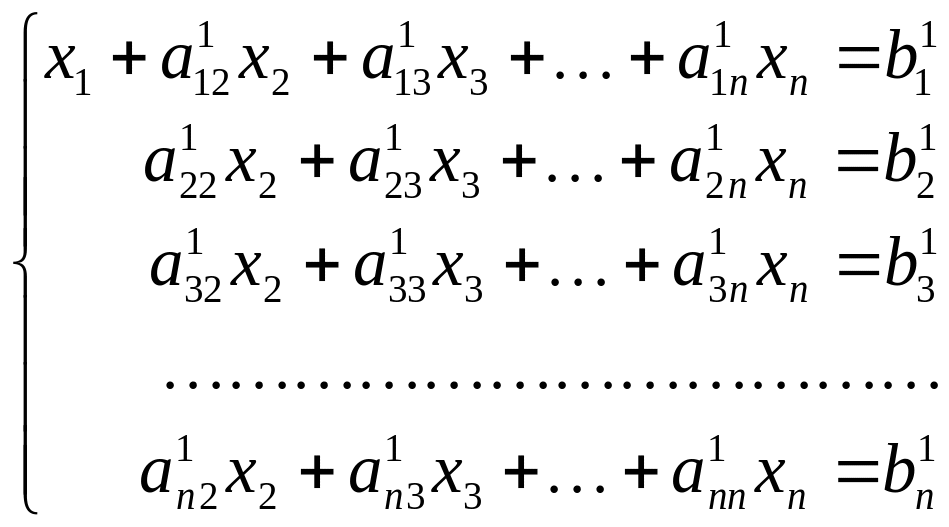 .
.
Далее процесс повторяется. За ведущее берется второе уравнение и исключается неизвестное x2 из всех уравнений, начиная с третьего
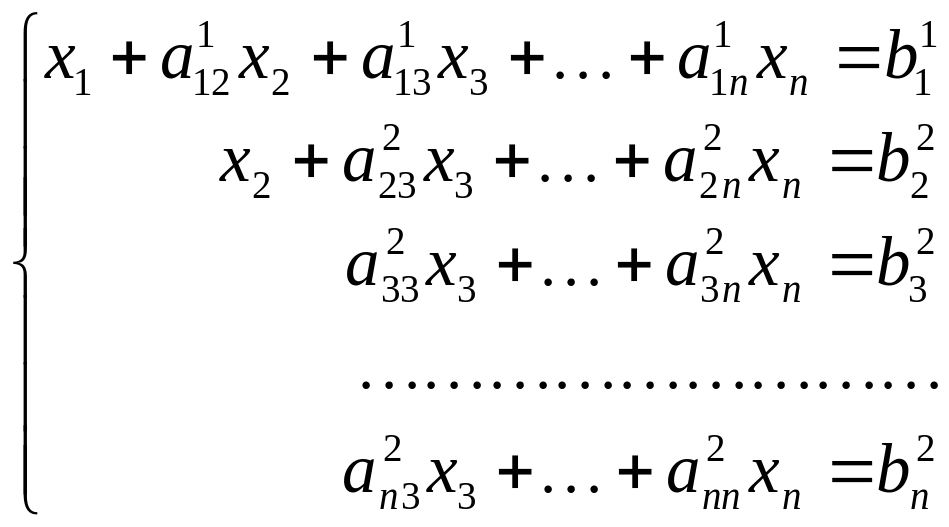 .
.
Таким образом, за n шагов система уравнений последовательно сводится к треугольному виду, при этом для последнего уравнения выполняется только операция нормирования:
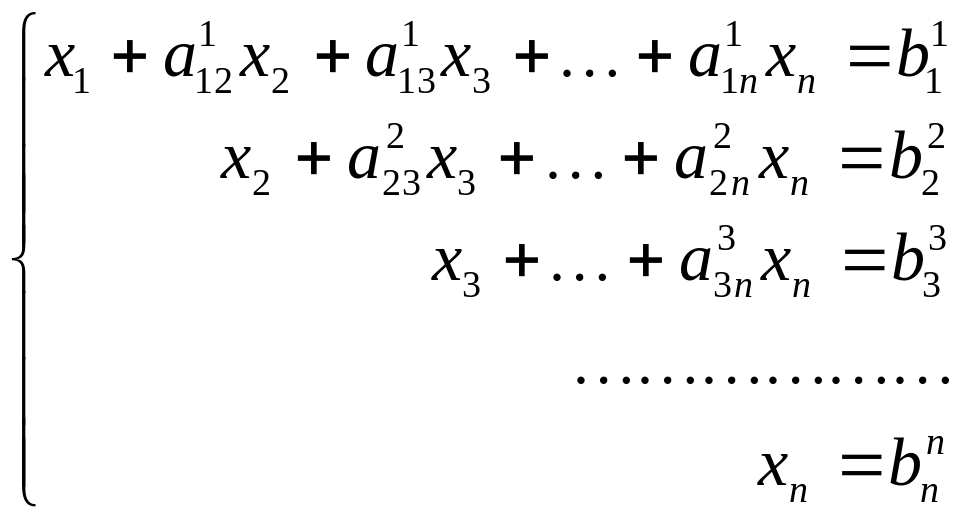 .
.
Полученная система с верхней треугольной матрицей может быть легко разрешена относительно неизвестных. Последнее уравнение системы определяет значение xn, что позволяет определить xn–1 из предпоследнего уравнения как
![]() .
.
Выполняя аналогичные подстановки найденных неизвестных в вышестоящие уравнения, удается определить все компоненты решения xn–2,..., x2, x1.
Метод
Гаусса даёт точное решение, если все
исходные данные точны и все вычисления
производятся точно. На практике, при
выполнении вычислений, неизбежно
проводятся округления. Ошибка округлений
вносит погрешность в решение метода
Гаусса. Таким образом, при операциях с
округленными десятичными числами метод
Гаусса даёт не точное решение xт
системы линейных алгебраических
уравнений, а некоторое приближённое
решение
![]() ,
где
,
где
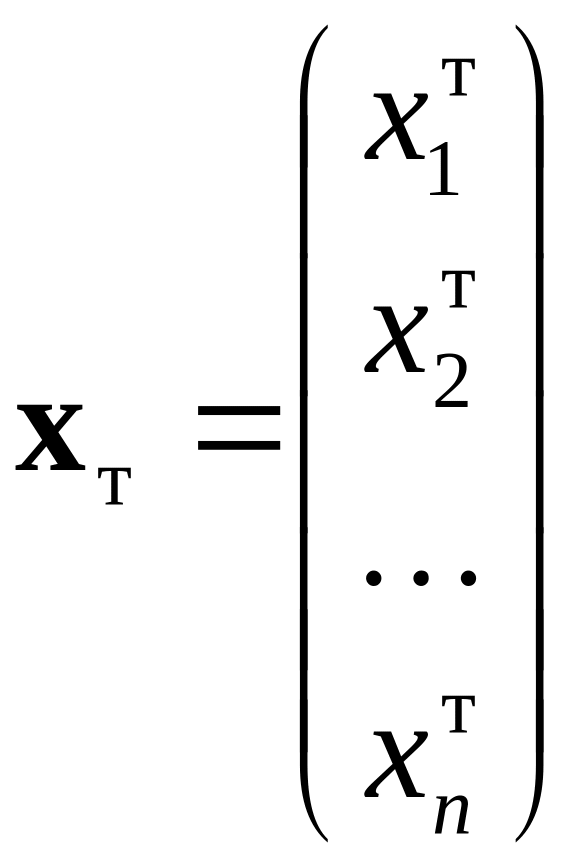 ,
,
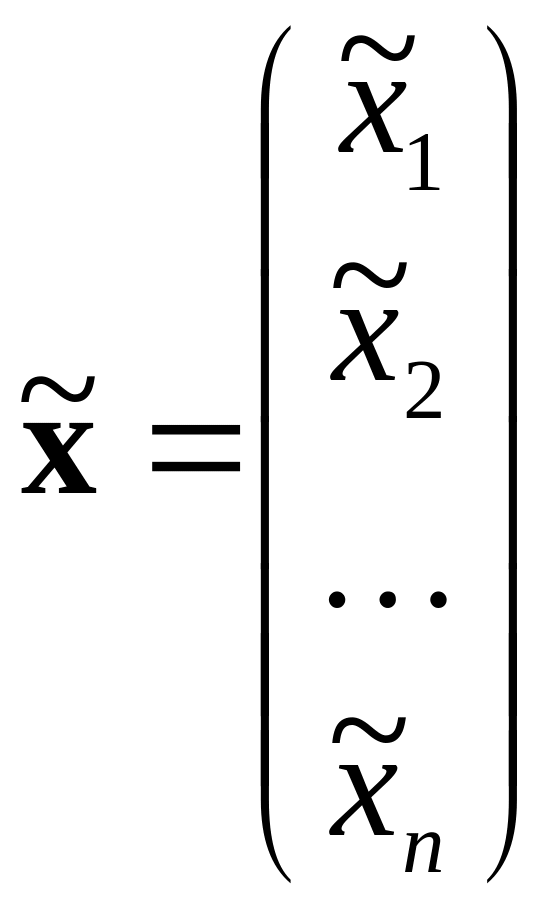 .
.
Степень отличия приближённого решения от точного определяется длиной разрядной сетки ЭВМ: чем больше разрядов в ней учитывается, тем это отличие меньше.
При определении погрешности вектора решения необходимо учитывать, что его компоненты в общем случае могут иметь разную погрешность. В силу этого погрешность решения принято оценивать по его норме
![]() или
или
![]() или
или
![]() ,
,
где
двойные модульные скобки
![]() обозначают норму вектора.
обозначают норму вектора.
Для
определения величины погрешности
полученного решения
![]() на практике используют следующий
алгоритм вычисления её главной части.
Сначала по имеющемуся решению
пересчитывается вектор правых частей
системы
на практике используют следующий
алгоритм вычисления её главной части.
Сначала по имеющемуся решению
пересчитывается вектор правых частей
системы
![]() ,
,
а затем посредством повторного решения системы уравнений
![]()
находится
вектор погрешностей
![]() .
С его помощью определяется как реальная
абсолютная погрешность полученного
решения
.
С его помощью определяется как реальная
абсолютная погрешность полученного
решения
![]() или
или
![]() или
или
![]() ,
,
так и его относительная погрешность
![]() .
.
Величина погрешности решения системы уравнений, получаемого методом Гаусса, зависит от двух основных факторов. Первый из них, как это было сказано выше – длина разрядной сетки, используемой в процессе вычислений, а второй – обусловленность матрицы системы. Обусловленность матрицы можно рассматривать как степень её чувствительности к накоплению ошибок округления в процессе преобразований. Снижение величины погрешности решения может быть достигнуто увеличением длины разрядной сетки. Повлиять на величину погрешности посредством изменения степени обусловленности матрицы системы невозможно, так как она является одной из её характеристик и изменение степени обусловленности матрицы требует изменения самой матрицы.
