Метод простых итераций

Метод основывается на приведении исходной системы к форме , где D – квадратная матрица, полученная из матрицы A, а p – вектор-столбец, полученный из b. Это преобразование может быть выполнено многими способами. Например, путем разрешения i-го уравнения относительно i-го неизвестного:

при этом элементы матрицы D и вектора p

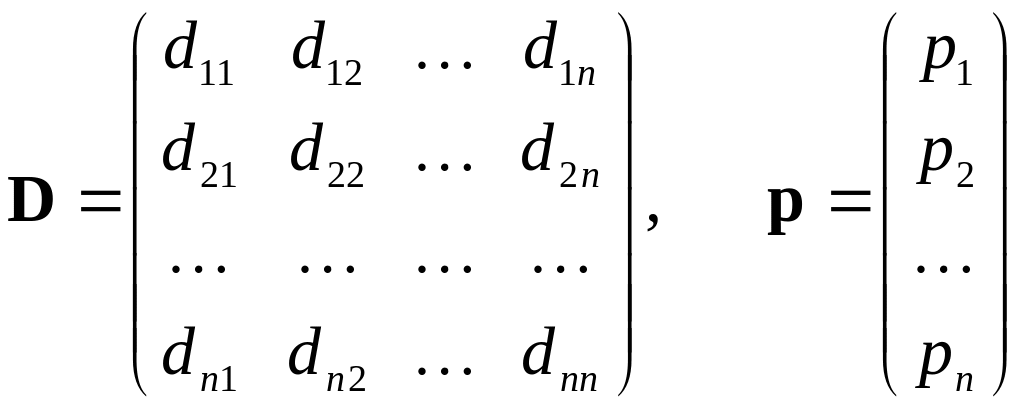
будут вычисляться следующим образом

.

Далее процесс уточнения корня строится по итерационной схеме

,

,

………………

,

……………….

где x₀ – начальное приближение вектора решения системы. То есть

,

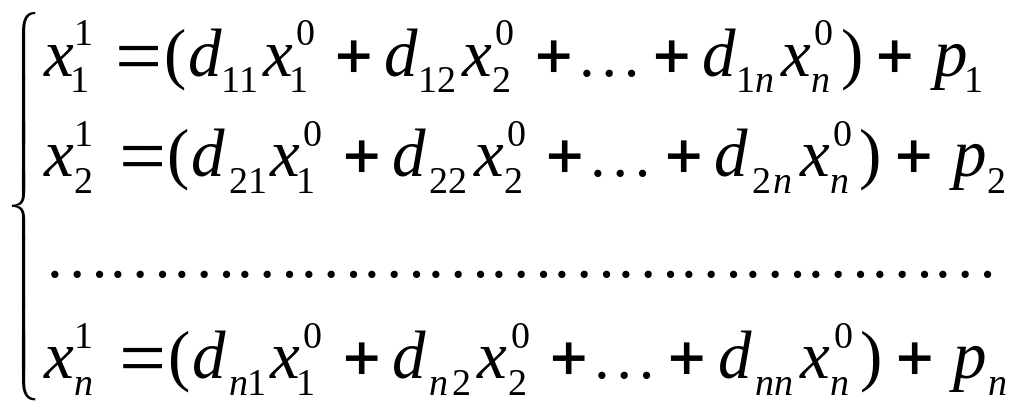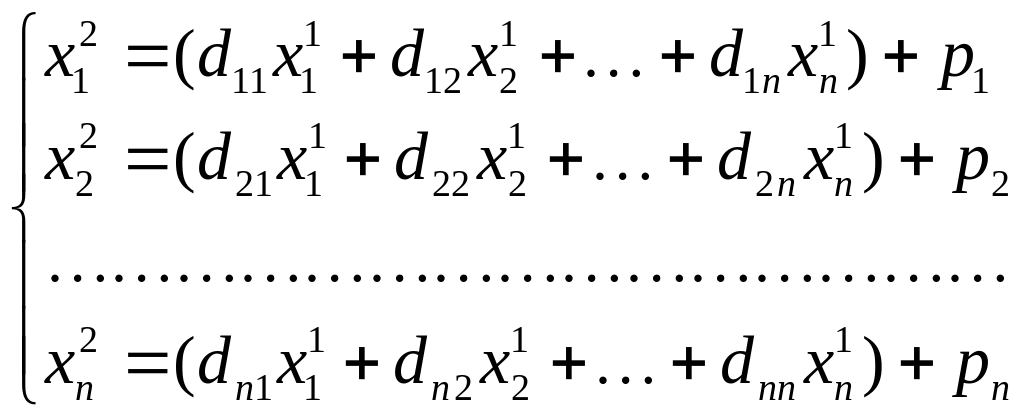
и так далее.

Если последовательность векторов x_k (k = 0,1,...) имеет конечный предел (тоже вектор), то итерационный процесс сходится к точному решению системы x_т за бесконечно большое число шагов. Абсолютная и относительная погрешности найденного вектора решения системы уравнений на k-ом шаге (x_k) могут быть получены из выражений

, ,

где в качестве нормы матрицы D можно использовать любое из трёх соотношений

, , .

Кроме приведённого выражения для абсолютной погрешности существуют другие формы её записи

, .

Формулы для вычисления погрешности вектора решения системы линейных алгебраических уравнений требуют нахождения нормы матрицы системы, поэтому на практике часто итерации завершают при выполнении одного из условий

или ,

где δ_абс и δ_отн – задаваемые абсолютная и относительная разницы между соседними приближениями вектора решения, соответственно. В этом случае надо помнить, что истинная погрешность определения решения может заметно отличаться от δ_абс или δ_отн. Поэтому после завершения поиска решения необходимо вычислить истинное значение его погрешности по приведённым выше формулам для ε_абс или ε_отн.

Встречаются ситуации, когда последовательность вычисляемых векторов x_k (k = 0,1,2,...) не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения системы уравнений. Для того, чтобы последовательность векторов x_k (k = 0,1,2,...) при любом начальном векторе x₀ сходилась к точному решению системы, надо выбрать матрицу D так, чтобы её норма была меньше единицы.

Если описанный выше приём формирования итерационной схемы не позволяет получить матрицу D, которая подчиняется условию сходимости, а матрица А – симметрична и положительно определена, то можно поступить следующим образом. Исходная система линейных алгебраических уравнений

приводится к эквивалентному виду

путем переноса произведения Ax в правую часть уравнения, умножения обеих частей уравнения на константу  и добавления к ним вектора x. В результате этого преобразования получается итерационная схема

,

где

.

Здесь под матрицей E понимается единичная матрица, а параметр _k может вычисляться с использованием выражения

,

где

, , .

Подбирая таким способом коэффициент λ_k на каждом шаге процесса итераций, удается получить матрицы D_k, подчиняющиеся условию сходимости. Описанный приём называется методом простых итераций с релаксацией.

Если система уравнений

имеет матрицу A, которая не является симметричной и положительно определённой, то надо произвести её симметризацию. Она заключается в умножении левой и правой частей системы на транспонированную матрицу A^T

,

что приводит исходную систему к системе

,

где

,

в которой матрица H симметрична и положительна определена.

Метод Зейделя (L.Seidel, 1874)

Этот метод является разновидностью метода простых итераций. Исходная система приводится к такому же виду, как и в методе простых итераций, но процесс итераций организуется иным образом. Как только на k-ой итерации вычислена i-я компонента вектора x_k, её значение используют для вычисления последующих компонент , ,..., этого вектора, не дожидаясь начала следующей итерации. Например

.

Вопрос о сходимости метода Зейделя, в общем виде, является открытым. Однако известно, что выполнение условия сходимости метода простых итераций гарантирует сходимость метода Зейделя. При этом благодаря особенностям итерационной схемы, метод Зейделя позволяет за то же количество шагов, что и метод простых итераций, получать более точный результат.

Если при решении системы уравнений методом Зейделя итерационный процесс расходится, то могут использоваться описанные выше приемы с релаксацией и симметризацией системы уравнений.

В качестве примера применения метода Зейделя можно рассмотреть задачу поиска решения следующей системы уравнений

с относительной разницей между соседними приближениями вектора решения не более 0.01 и с оценкой его погрешности.

Следуя алгоритму метода Зейделя, требуется преобразовать исходную систему уравнений к виду

,

где

,

и выполнить её проверку на сходимость

Так как условие сходимости выполняется, то итерационный процесс может быть начат с любого удобного значения вектора x. В качестве начального приближения обычно принимается нулевой вектор

.

Первая итерация

Вторая итерация

Третья итерация

Четвёртая и пятая итерации дают соответственно

, ,

, .

Определение погрешности решения по последней итерации

,

.

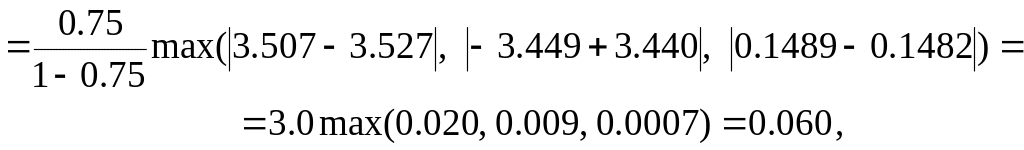
При реализации алгоритма метода Зейделя для решения рассмотренного выше примера в программе Excel может быть применена расчётная таблица 1.

Таблица 1.

i	xi
1				0	–	–
2
3	……	……	……	……	…….	…………..

Ниже на рис.2 представлены результаты расчётов в программе Excel по предлагаемой таблице. Для вычисления максимума из нескольких чисел здесь использована функция МАХ из числа встроенных в программу Excel статистических функций.

Рис.2.

О выборе метода решения систем уравнений

Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, метод Гаусса позволяет получить решение за конечное число шагов. Для этого требуется выполнить n(n² + 3n – 1)/3 операций умножения и деления и n(n – 1)(2n + 5)/6 операций сложения и вычитания, количество которых при больших порядках системы (n > 100) можно принять равным n³/3 в обоих случаях. Однако его методические ошибки, связанные с размером разрядной сетки вычислений, резко нарастают с увеличением порядка системы и не позволяют применять его для систем высоких порядков без использования специальных приёмов.

Итерационные методы позволяют получать решение систем бóльшего порядка. Для выполнения каждой итерации с их помощью необходимо выполнить n(n + 1) операций умножения и деления и столько же операций сложения и вычитания. При больших порядках системы уравнений (n > 100) их количество можно принять равным n². Из сравнения трудоёмкости итерационных методов и метода Гаусса следует оценка, которой можно руководствоваться при окончательном выборе метода решения системы при необходимости его многократного нахождения. Если количество итераций, требуемое для получения решения системы итерационными методами, не превышает n/3, то выгоднее применять их, а не методы типа Гаусса. Однако здесь следует помнить, что итерационные методы требуют, чтобы матрица системы обладала определёнными свойствами, обеспечивающими их сходимость. Необходимо также отметить, что выполнение этих требований часто не гарантирует высокой скорости их сходимости.