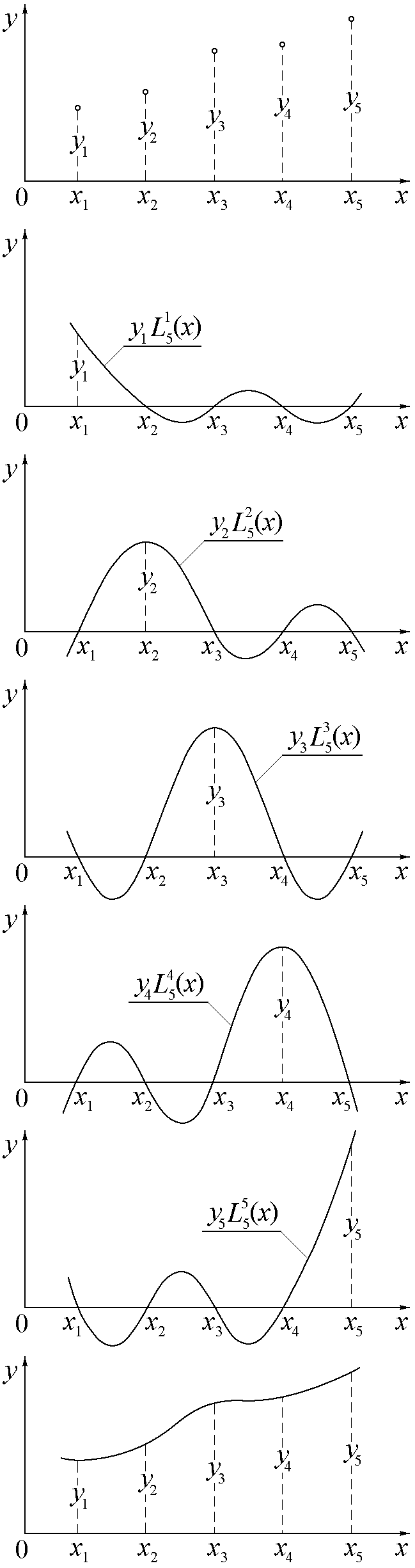Кусочно-линейная интерполяция

К

Рис.2.

усочно-линейная интерполяция состоит в представлении таблично заданной функции на каждом отрезке между абсциссами узловых точек линейной зависимостью y = a₁+ a₂x так, как это показано на рис.2. Коэффициенты a₁ и a₂ определяются для каждого отрезка [x_i–1, x_i] в отдельности из условий

.

В результате кусочно-линейная приближающая функция на отрезке [x_i–1, x_i] имеет вид

,

и является непрерывной, однако её первая производная оказывается кусочно-непрерывной функцией, которая в каждом узле интерполяции имеет точку разрыва первого рода. Это часто накладывает существенные ограничения на её дальнейшее использование.

x	0	1	2	3
y	2	0.5	1	4

Рассмотрим работу метода на примере кусочно-линейной интерполяции таблично заданной функ­ции и поиска её значения при аргументе х = 1.6.

Для решения этой задачи строятся линейные функции для каждого отрезка между узловыми точками таблицы:

для отрезка [0, 1] между первой и второй точками

,

для отрезка [1, 2] между второй и третьей точками

,

для отрезка [2, 3] между третьей и четвёртой точками

,

Таким образом, табличная функция в случае кусочно-линейной интерполяции представляется в виде функции

Значение интерполирующей функции в заданной точке x = 1.6, принадле­жа­щей отрезку [1, 2] будет

y(1.6) = 0.5 + 0.5(1.6 – 1) = 0.8.

Ниже на рис.3 представлен фрагмент рабочей книги Excel с реализацией метода кусочно-линейной интерполяции. При построении графика приближающей функции аргумент х изменяется с шагом 0.2, а значения функции вычисляются по общей формуле, адаптированной под конкретные значения диапазонов аргумента.

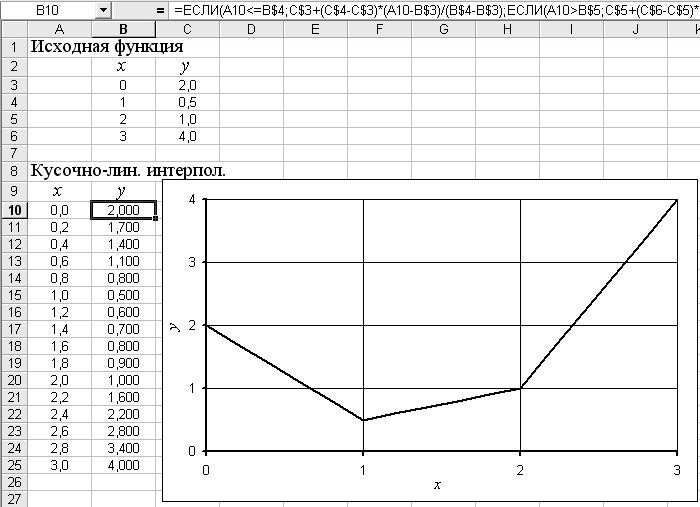
Рис.3.

Как видно из рисунка для аргумента x = 1.6 расчёты, проведенные программой Excel, дали значение 0.8.

Многочлен Лагранжа (J.L.Lagrange, 1795)

Представляет собой случай полиномиального представления приближающей функции, когда она ищется в виде линейной комбинации базисных функций _k(x), которые должны быть определены для всего отрезка интерполяции [x₁, x_n], линейно независимы, и их количество должно быть равно числу узлов таблично заданной функции

.

Коэффициенты a₁, a₂, ..., a_n определяются исходя из условий равенства значений приближающей и исходной функций при табличных значениях аргумента, что сводит задачу к системе n линейных алгебраических уравнений относительно них, а в качестве функций _k(x) используются полиномы (n–1) степени

,

которые для пяти узловых точек записываются в виде

,

,

,

,

.

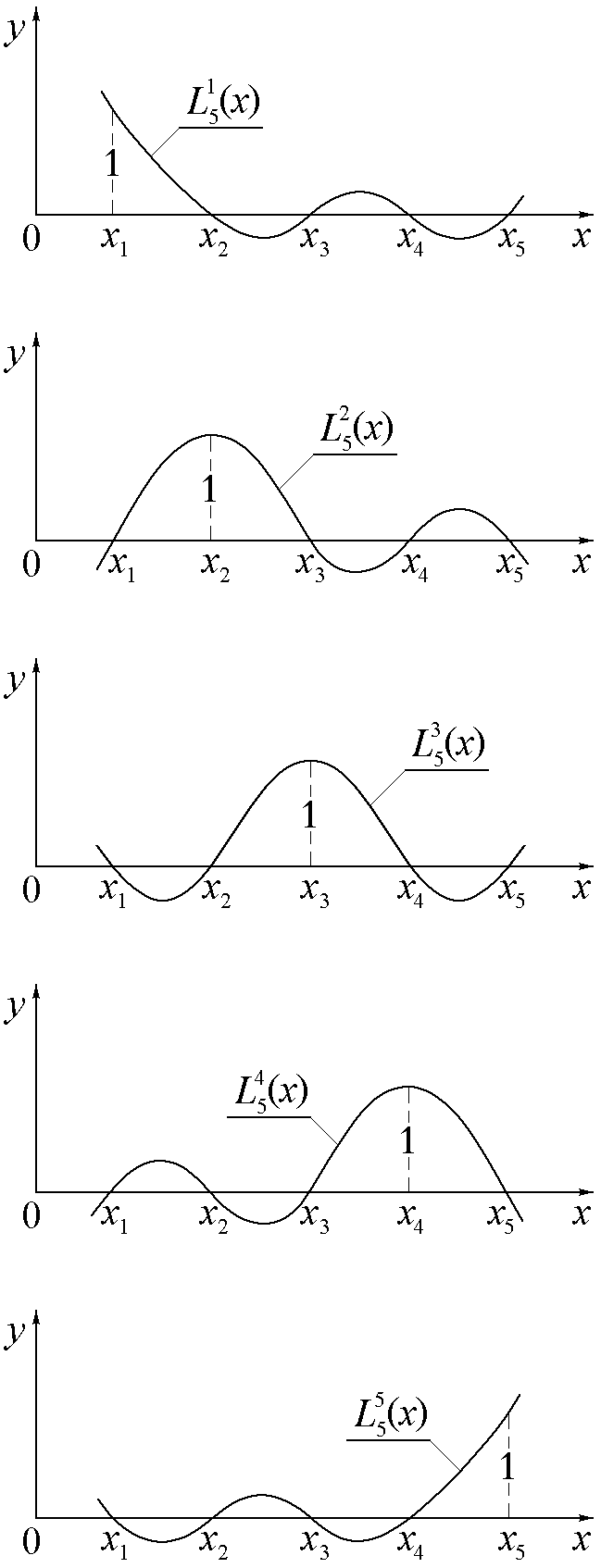
Для каждого полинома характерно то, что для всех значений x_i в узловых точках он принимает нулевые значения, кроме k-ой, где его значение равно единице.

Графики этих полиномов пред­ставлены на рис.4. П Рис.4. ри таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции, а сама она приобретает харак-

Рис.5.

терный для многочлена Лагранжа вид:

.

Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.5.

Рассмотрим работу метода на приведенном выше примере. Сначала строятся четыре базовых полинома:

,

,

,

.

Они позволяют записать интерполирующий многочлен Лагранжа в виде

Для аргумента x = 1.6 многочлен Лагранжа даёт

Ниже на рис.6 представлен фрагмент рабочей книги Excel с реализацией интерполяции с помощью многочлена Лагранжа.

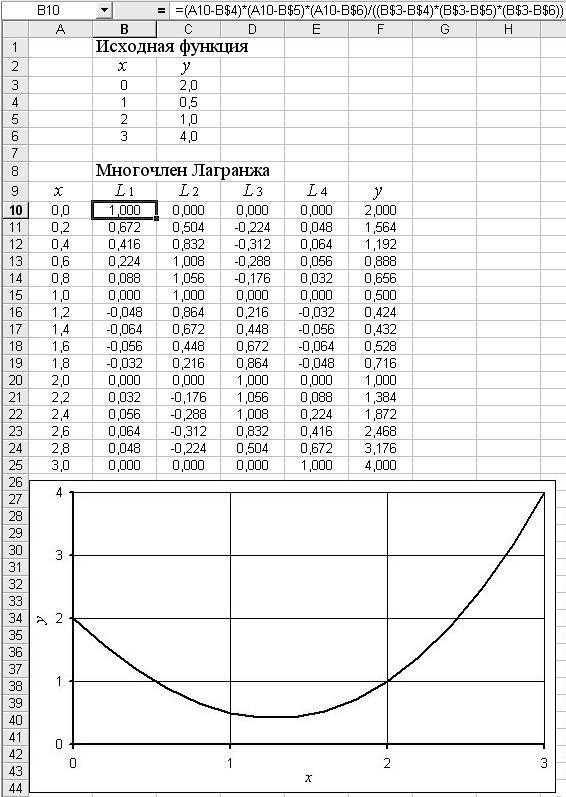
Рис.6.

Как видно из рисунка для аргумента x = 1.6 многочлен Лагранжа дал значение 0.528.

Для контроля правильности вычислений многочлена Лагранжа полезно строить графики базовых полиномов. Для рассматриваемого примера они приведены на рис.7.

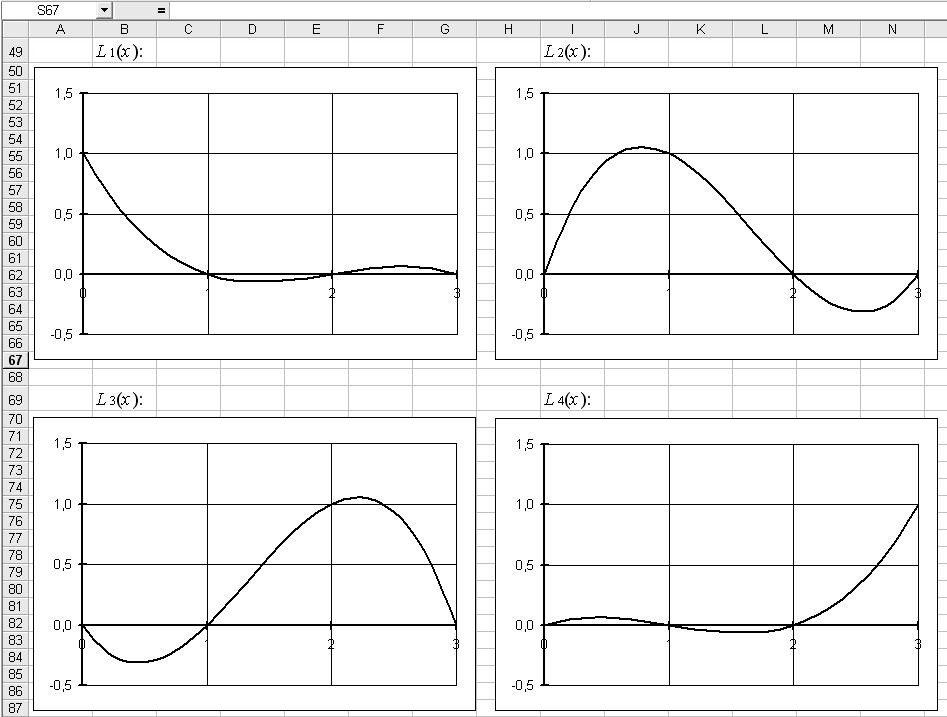
Рис.7.