П

Открытие релятивистского волнового уравнения для электрона

осле своего возникновения квантовая механика и теория относительности некоторое время развивались независимо друг от друга. Однако необходимость их объединения была очевидной, и не только потому, что требовалось развить методы квантового описания частиц, движущихся с субсветовыми скоростями. Даже такой традиционный объект применения методов квантовой механики, как атом, нельзя полностью описать без учета испускания и поглощения атомом фотонов, являющихся сугубо релятивистскими частицами. Поэтому вопросу об обобщении квантовой механики, изначально сформулированной в нерелятивистской форме, на релятивистский случай уделялось большое внимание.

26 апреля 1926 года была опубликована статья О. Клейна «Квантовая теория и пятимерная релятивистская теория», в которой было предложено релятивистское волновое уравнение, переходящее в пределе в уравнение Шредингера. Вскоре после статьи Клейна были опубликованы работы В. А. Фока «К шредингеровской волновой механике» (от 11 июля) и «Об инвариантной форме волнового уравнения и уравнений движения для заряженной частицы» (от 30 июля). Полученное Фоком волновое уравнение совпадало с уравнением, предложенным Клейном, поэтому его стали называть уравнением Клейна-Фока (позже оно утвердилось в физике под названием уравнения Клейна-Гордона-Фока).

Нерелятивистское временное уравнение Шредингера для свободной частицы

(19.29)

может быть получено из классического соотношения с помощью формальной замены величин E и на соответствующие квантовомеханические операторы и . Для получения релятивистского волнового уравнения была использована та же схема. Применение указанной формальной замены к известному релятивистскому соотношению

(19.30)

и привело к уравнению Клейна-Гордона-Фока:

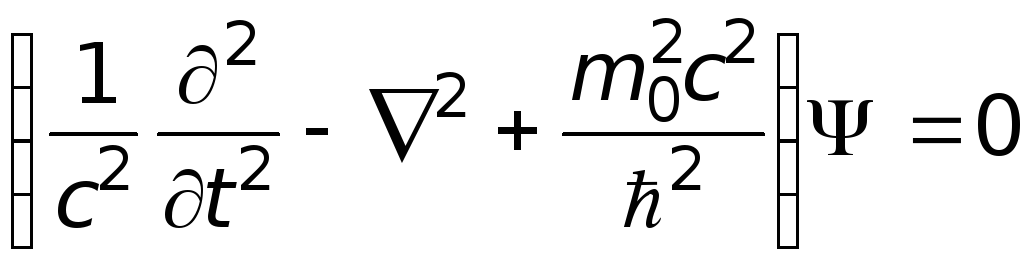. (19.31)

Волновая функция в уравнении (19.31) зависела от трех пространственных координат и времени, но не содержала спиновых переменных. Поэтому при преобразованиях Лоренца однокомпонентная функция x,y,z,t преобразовывалась как скаляр. Указанное трансформационное свойство позволяло сделать вывод о том, что частица, описываемая уравнением (19.31), должна обладать нулевым спином.

Из уравнения (19.31) вытекало, что роль плотности вероятности должна играть величина

, (19.32)

не являющаяся положительно определенной (каковой обязана быть плотность вероятности). Поэтому решение уравнения Клейна-Гордона-Фока нельзя было истолковать как амплитуду вероятности. Выход из этого затруднения был найден в квантовой теории поля, где уравнение (19.31) рассматривается как уравнение для оператора скалярного поля .

Чтобы выражение для плотности вероятности было положительно определенным, требовалось исключить из него производные по времени . Для этого было необходимо, чтобы искомое волновое уравнение содержало производные только первого порядка. Поскольку во все релятивистски-инвариантные выражения пространственные координаты и время должны входить симметричным образом, то искомое релятивистски-инвариантное волновое уравнение должно было содержать только первые производные по координатам и времени.

На основе этих соображений Дирак в двух работах под общим названием «Квантовая теория электрона» (от 2 января и 2 февраля 1928 года) предложил релятивистское волновое уравнение для электрона, которое, в отличие от уравнения второго порядка Клейна-Гордона-Фока, являлось дифференциальным уравнением первого порядка:

, (19.33)

где операторы проекций импульса связаны с производными по координатам посредством обычных соотношений . Уравнение (19.33) формально совпадало с уравнением Шредингера (19.29) в предположении, что выражение в круглых скобках есть оператор Гамильтона . Но тогда связь между оператором и проекциями импульса , , должна была выражаться соотношением

, (19.34)

аналогичным соотношению (19.30) в теории относительности. Для выполнения этого требования оказалось необходимым, чтобы величины , , и , входящие в уравнение Дирака (19.33), удовлетворяли условиям антикоммутации:

; ;

; ; (19.35)

;

и условию

. (19.36)

Дирак показал, что всем этим условиям невозможно удовлетворить в рамках одного дифференциального уравнения для однокомпонентной функции . Величины , , и , удовлетворяющие условиям (19.35) и (19.36), оказались квадратными четырехрядными матрицами, которые могли быть выражены через двухрядные матрицы Паули

; ; ; (19.37)

и единичную матрицу в виде:

; ; ; .

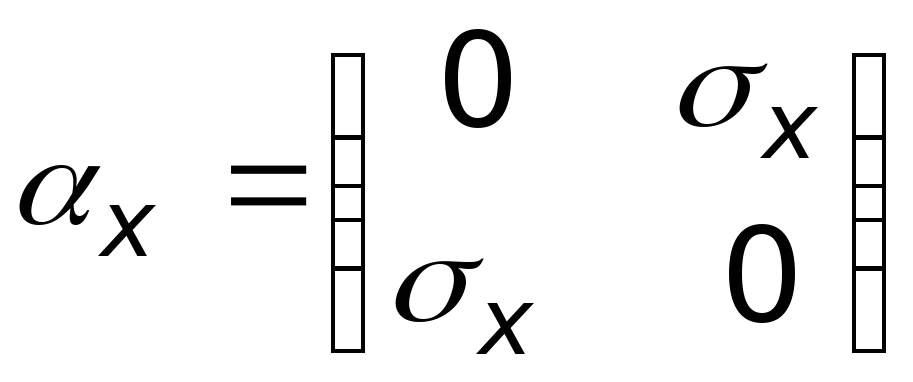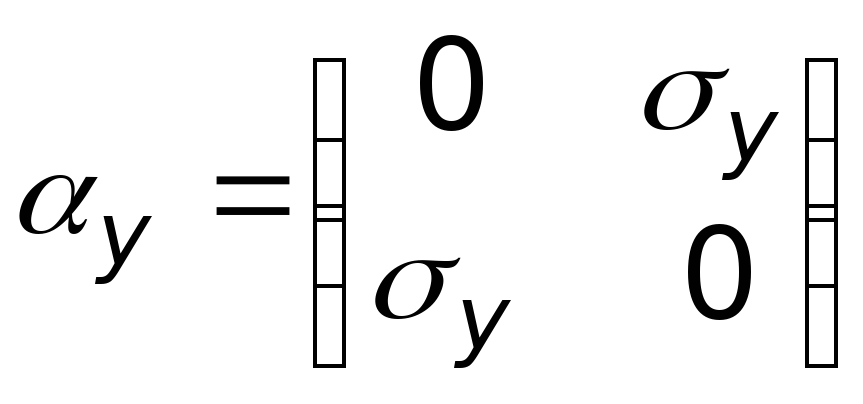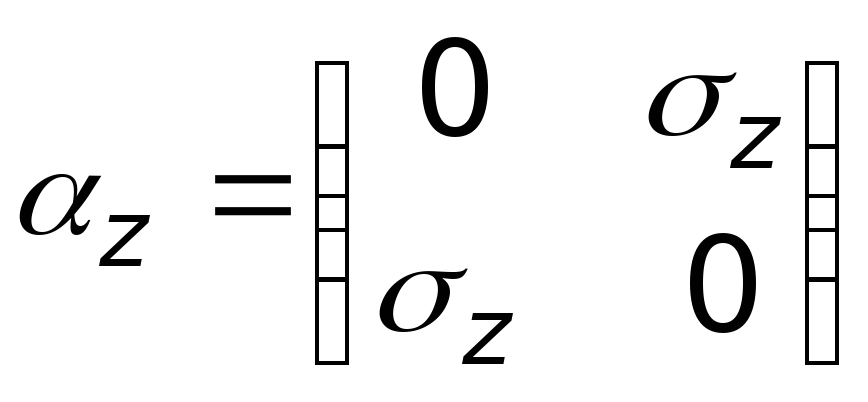(19.38)

При этом релятивистская волновая функция оказалась четырехкомпонентной

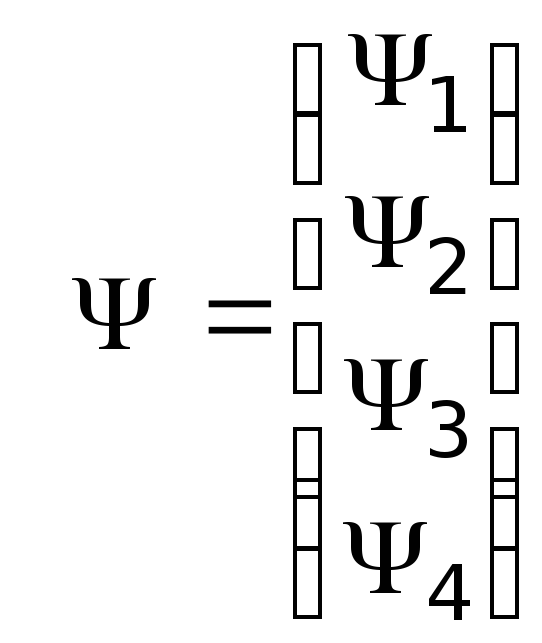, (19.39)

а предложенное Дираком уравнение (19.33) являлось фактически системой четырех уравнений для четырех функций ₁, ₂, ₃, ₄ от координат x, y, z и времени t:

;

;

; (19.40)

;

Плотность вероятности в теории Дирака являлась существенно положительной величиной:

.

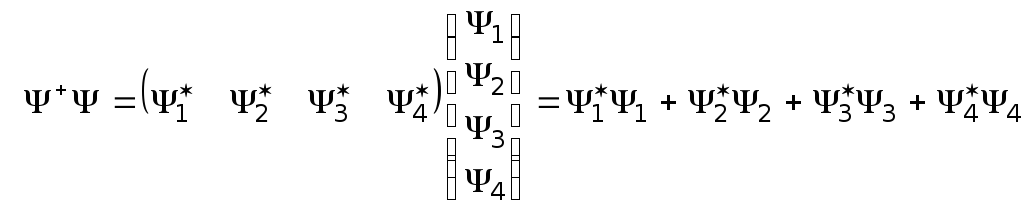(19.41)

Линейность уравнения Дирака означала выполнение одного из основных принципов квантовой механики – принципа суперпозиции. Из этого, а также из вероятностной интерпретации волновой функции  следовало, что остается в силе обычная схема построения формализма квантовой механики. Это означало, что в теории Дирака, как и в нерелятивистской квантовой механике, интегралом движения является физическая величина, оператор которой не зависит от времени явно и коммутирует с оператором Гамильтона. Было очевидным, что в релятивистской квантовой теории, как обычно, должен сохраняться полный момент импульса свободного электрона. Однако операторы орбитального момента и его z-проекции и не коммутировали с оператором Гамильтона, выбранным в виде

. (19.42)

Было установлено, что в теории Дирака сохраняются величина и z-проекция полного момента , являющегося векторной суммой орбитального и некоторого дополнительного момента . Этот дополнительный момент играл роль собственного момента импульса свободного электрона, а собственные значения его z-проекции составляли . Таким образом, уравнение Дирака в неявном виде уже содержало спин электрона.

В случае свободного движения частицы система уравнений (19.40) приводила к известному релятивистскому соотношению (19.30). Это соотношение допускало как положительные, так и отрицательные значения энергии:

. (19.43)

В частности, для покоящейся частицы получалось: . В рамках доквантовой физики это обстоятельство не приводило к осложнениям, поскольку все физические величины считались непрерывными. Интервал значений энергии оказывался запрещенным, поэтому переход из области отрицательных энергий в область положительных был невозможен. При этом принималось, что имеющим физический смысл решениям соответствуют положительные значения энергии, а отрицательные значения просто отбрасывались.

Однако для квантовой теории была характерна именно дискретность переходов с одного уровня энергии на другой и, в частности, не были запрещены переходы между состояниями с положительной и отрицательной энергией. Таким образом, решения уравнения Дирака, соответствующие отрицательным энергиям, не могли быть отброшены без нарушения основных принципов квантовой механики.

Чтобы обойти эту трудность, Дирак в 1930 году выдвинул гипотезу о том, что физический вакуум является состоянием пространства, в котором все состояния с отрицательными энергиями заняты электронами, а все состояния с положительными энергиями – свободны. Число состояний с отрицательной энергией бесконечно велико; в каждом таком состоянии, согласно принципу Паули, находится один электрон. Дирак предложил считать, что состояния с отрицательной энергией образуют физически ненаблюдаемый фон. Если же одному из электронов с отрицательной энергией сообщить энергию, превышающую ширину области запрещенных значений 2m₀c², то он перейдет в область положительных энергий и будет вести себя, как обычный электрон. При этом в бесконечном резервуаре электронов с отрицательными энергиями возникает незанятое состояние – «дырка», которая проявляется на опыте как частица с положительным зарядом.