Однородные уравнения первого порядка

Прежде чем перейти к рассмотрению вопроса о решении однородных уравнений первого порядка познакомимся с понятием однородных функции.

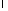Определение 1. Функция называется однородной функцией-го измерения относительно переменныхи, если при любомсправедливо тождество

.

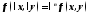Так, например, функция однородная функция первого измерения, т.к.;

функция однородная функция нулевого измерения, т.к.;

функция неоднородная функция, т.к.однородная функция первого измерения, аоднородная функция четвёртого измерения.

Определение 2. Уравнение первого порядка называется однородным относительнои, если функцияесть однородная функциянулевого измерения относительно и.

Однородные уравнения первого порядка приводятся к уравнениям с разделяющимися переменными с помощью подстановки

Уравнение вида 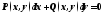будет однородным тогда и только тогда, когда функцииибудут однородными функциями одного и того же измерения.

Например, однородное уравнение;

неоднородное уравнение.

Замечание: Уравнения вида приприводятся к однородным подстановкойгдеточка пересечения прямыхи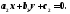Таким образом, для определенияинеобходимо решить систему уравнений:

Если же , то подстановкапозволяет разделить переменные.

Линейные уравнения первого порядка

Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной.

Линейное уравнение первого порядка имеет вид:

(1)

где заданные непрерывные функции отили постоянные числа.

Решение линейного уравнения будем искать в виде произведения двух функции от :

(2)

где . Дифференцируя обе части последнего выражения, получим:

(3)

Значения подставим в данное уравнение (1)

или

Выберем функцию такой, чтобы

, (4)

тогда . (5)

Решив сначала уравнение (4) и затем уравнение (5), найдём значения и. Подставив значенияив (2) найдём решение уравнения (1).

Замечание: Уравнение вида , (6)

где и , называется уравнением Бернулли.

Уравнение Бернулли приводится к линейному следующим преобразованием: разделим все члены уравнения на

(7)

и произведём замену . (8)

Тогда . (9)

Подставив значения (8) и (9) в (7), получим или

(10)

Решив линейное уравнение (10) и учитывая, что ,найдём решение уравнения (6).

_{Заметим, что уравнение (6) часто можно решить как и линейное уравнение с пом}ощью подстановки

Уравнение в полных дифференциалах

Определение. Уравнение

называется уравнением в полных дифференциалах, есл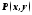и и- непрерывные, дифференцируемые функции, для которых выполняется соотношение

Левая часть такого уравнения есть полный дифференциал некоторой функции . Если это уравнение переписать в виде, то его общее решение определяется равенствомФункцияможет быть найдена по формуле

.

Интегрирующий множитель

Пусть левая часть уравнения не есть полный дифференциал. Иногда удаётся подобрать такую функцию, после умножения на которую всех членов уравнения левая часть уравнения становится полным дифференциалом.

Общее решение полученного таким образом уравнения совпадает с общим решением первоначального уравнения; функция называетсяинтегрирующим множителем данного уравнения.

Для того чтобы найти умножим обе части уравнении на неизыестный пока интегрирующий множитель:

Для того чтобы последнее уравнение было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:

т.е. или. После деления обеих частей последнего уравнения на, получим:

.

Задача нахождения из последнего уравнения ещё труднее, чем первоначальная задача интегрирования данного уравнения. Только в некоторых частных случаях .

удаётся найти функцию

Пусть, например, данное уравнение допускает интегрирующий множитель, зависящий только от . Тогда

и для отыскания мы получаем обыкновенное дифференциальное уравнение

Откуда

Аналогично, если у данного уравнения существует интегрирующий множитель, зависящий только от , то он находится по формуле