80.Вычисление площади поверхности

Пусть какая-то часть пов-тиобладающая

тем свойством что и с достаточно малым диаметром проектирования на касательную плоскость в любой(.)этой части взаимно однозначны. Перенеся начальную координату в это(.)перейдем к новым

координатам .За плоскость

возьмем касательную плоскость к поверхности в(.)М ,за ось -нормаль в этой(.).Формулы преобразования примут вид:;

;

;

Определитель равен: ;

;

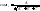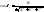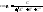.Имеются непрерывные функции 4-х независимых переменных U,V, В ОБЛАСТИПРИ.

Эта функция принимает вид: .Таким образом.То есть это и есть площадь поверхности.

№81( Поверх. Инт.1 рода. Вычисление.)

Поверх. Инт. 1 рода предст. Собой обобщение ∫∫(двойн.инт.) как криволин-й Инт. 1рода явл. Обобщением определён. Инт-ла.Пусть в т-ках некот. Двусторонней гладкой поверхности S, ограниченной кусочно-гладким контуром определена ф-ция f(M)=f(x,y,z).Разобъём поверх-ть S с помощью сети произволь-х проведённых кусоч.-глад. Кривых на части S1S2…Sn.

Возьмём в каждой части 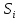произв. Точку().

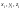Вычислим знач-е ф-ции в этой точке:

f()=f().

Умножим это значение на площадь соответствующей части поверх-ти.

Составим сумму всех таких произведений:

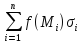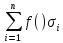==Эту сумму называют инт. суммой.

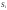(ОПР)Конечный предел интегральной суммы при стремлении диаметров всех частей-х к 0 наз-ся поверх-м инт-м 1 рода ф-ции f(x,y,z) по поверх-ти S, т.е. I ==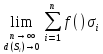

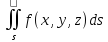
Свойства поверхностного интеграла 1-го рода.

Основными свойствами поверхностного интеграла 1 го рода являются:

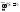– , где – площадь поверхности;

– (линейность) если и— произвольные постоянные числа, функци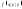ииинтегрируемы на поверхности, то функция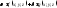также интегрируема на поверхностии справедливо равенство

;

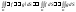– (аддитивность) если поверхность состоит из двух частейи,,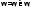 а пересечениеисостоит лишь из границы, их разделяющей, и функция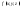интегрируема наи, то функция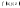также интегрируема на поверхностии справедлива формула:

;

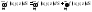– (монотонность) если на поверхности выполнено неравенств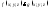о, то

;

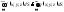– (оценка интеграла) ;

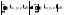– (теорема о среднем) если 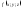непрерывна на поверхности, то на этой поверхности существует такая точка, что

,

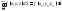где – площадь поверхности.

Вычисление:

Для сведения пов. инт-ла 1 рода к ∫∫ нужно заменить корд-ты x,y,z их выражениями через параметры U и, а элемент площади ds его выражением в криволин-х коорд-х.

пусть

1)(параметрич задание)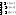, тогда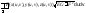, где

, ,.

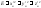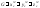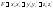2)Если поверх-ть S задана явным ур-ем Z=f(x,y),то

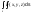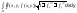=,D-проекция плоск-ти S на плоск-ть xy

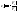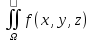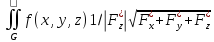3)(неявное задание)F(x,y,z)=0 ,;ds=dxdy

Приложения:

С помощью поверх инт 1 рода можно определять массы, моменты, коорд-ты центров тяжести для материаль-х поверхностей, вдоль которых распределены массы с единств. в каждой точке поверх-ти плоскостью.

Пусть вдоль поверх-ти S распределена масса с плотностью ,

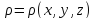Тогда масса всей поверх-ти:

m=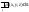статические моменты: Коорд-ты центра тяж-ти масс:

=

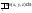
xc =Myz/m yc=Mzx/m zc=Mxy/m

=

=

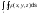
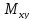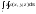
№82( Поверх. Инт.2 рода. Вычисление.)

(ОПР)

Конечный предел интегральной суммы

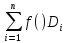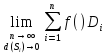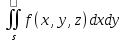
= при стремлении диаметров всех частей-х к 0 наз-ся поверх-м инт-м 2 рода от ф-ции f(x,y,z) распространённым на выбранную сторону поверх-ти S ,т.е. . I ==, где dxdy указывает на площадь проекции элем-та поверх-ти на плоск-ть xy.На плоск yz и zx соответственно,.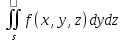

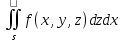Общий инт. 2рода – сумма 3-х част-х поверх-х инт-лов 2рода, т.е.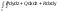, P,Q,R ф-ции определён-е в точках поверх-ти S Свойства поверхностного интеграла 2-го рода. Поверхностный интеграл 2-го рода обладает следующими свойствами:– для общего поверхностного интеграла 2-го рода справедливо равенство:

;

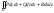
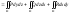– (линейность) если и— произвольные постоянные числа, функци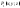ии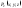интегрируемы по выбранной стороне поверхности, то функция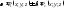также интегрируема по выбранной стороне поверхностии справедливо равенство:

;

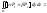
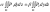– (аддитивность) если поверхность , из двух частейи,, а пересечениеисостоит лишь из границы, их разделяющей, и функцияинтегрируема по выбранным сторонами, то функциятакже интегрируема по выбранной стороне поверхностии справедлива формула

;

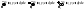– (оценка интеграла) если функции ,,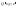интегрируемы по выбранной стороне двусторонней поверхностии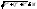во всех точках поверхности, то

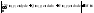
где – площадь поверхности;

– (ориентированность) если противоположная сторона к сторонеповерхности, то

.

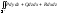
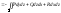Вычисление: Если инт-л берётся по верх. стороне поверх-ти, то 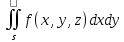сводится к инт-лу

1)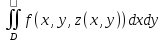, т.е

=

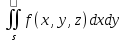Если инт-л берётся по ниж. . стороне поверх-ти, то 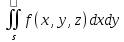сводится к инт-лу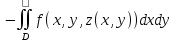, т.е.

=

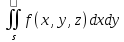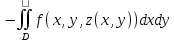
2) явно

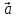=(P,Q,R), 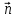=(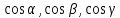),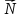=( -),при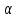<(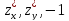), при>

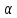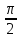
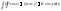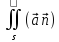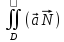==ds=dxdy

№83 Формула Стокса

Формула Стокса устанавливает связь между поверхностными интегралами и криволинейными интегралами.

Теорема. Пусть

1) –элементар-я относит-но осиповерх-ть, заданная ур-ем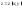, где ф-ции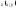,,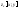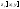– непрерывны в замкнутой обл., проекциина;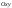

2) –контур, огранич-щий область,–его проекция на плоскость, являющаяся контуром, ограничивающим область;

3) ф-ции 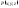,,непрерывны вместе со своими част. производными первого порядка на выбранной стороне поверхности.

Тогда имеет место формула Стокса

.

Следствие. Если

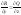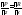, ,, то

1) ;

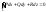2) подынтегральное выражение представляет собой полный дифференциал некоторой функции 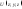, для которой:.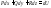

Формула Стокса справедлива для любой области, которую можно разбить на конечное число элементарных областей указанного вида.

Учитывая, что ,,,

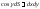формулу Стокса можно записать в виде:

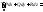
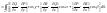№84 Формула Гаусса –Остроградского

Формула Остроградского-Гаусса устанавливает связь между поверхностными интегралами 2-го рода по замкнутой поверхности и тройными интегралами по пространственной области, ограниченной этой поверхностью.

Теорема 1 Пусть

1) – элементарная относительно осизамкнутая область, ограниченная поверхностью; 2) функции,,непрерывны вместе со своими частными производными первого порядка в области.

Тогда справедлива формула Остроградского-Гаусса

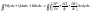Формула Остроградского-Гаусса справедлива для любой области , которую можно разбить на конечное число элементарных областей. Также формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов 2-го рода по замкнутым поверхностям.Для вычисления объема тела, ограниченного замкнутой поверхностью, используется формула: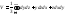