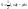- •1.Пространство rⁿ
- •2.Метрическое пространство, евклидово пространство.
- •3.Основные или важнейшие множества точек пространства
- •4.Функции n-переменных.
- •5.Сходимость в пространтсве Rn.
- •6.Предел функции нескольких переменных.
- •8.Повторные пределы.
- •9.Непрерывность функции нескольких переменных.
- •10.Непрерывность функции нескольких
- •11. Основрые свойства непрерывных функций нескольких переменных
- •12. Частные производные ф-ии нескольких переменных
- •13. Дифференцируемость ф-ии нескольких переменных
- •14. Дифференциал функции нескольких переменных
- •15. Достаточное условие дифференцируемости ф-ии нескольких переменных
- •16. Дифференцирование сложной ф-ии
- •17. Однородная функция. Теорема эйлера об однородных функциях
- •18. Инвариантность формы первого дифференциала функции нескольких переменных
- •19. Геометрический смысл дифференциуемости функции двух переменных
- •20. Производная по направлению
- •21.Частные производные высшего порядка.
- •22.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
- •23.Производные высших порядков.
- •26. Экстремум функции многих переменных.
- •27.Достаточные услов локальн экстрем ф-ций нескол перемен.
- •28. Критерий Сильвестра
- •29.Определение наибольшего и наименьшего значения
- •30.Не явные ф-ции.
- •31.Теорема о существ и диф-ти неявной ф-ции.
- •32.Вычисление частных производн неявно заданных ф-ций.
- •33.Неявные ф-ции определ систем функцион уравнений.
- •34. Зависимость ф-и нескольких переменных
- •35.Функциональные матрици
- •36. Усл.Экстремум
- •37.Метод неопредёлённых множетелей Логранжа.
- •38.Числовой ряд. Сходимость, расходимость рядов.
- •39.Необход признак сходим ряда.
- •40. Признак сравнения рядов
- •41.Признак Даламбера.
- •42.Признак Коши.
- •43. Интегральный признак Коши
- •44. Признак Лейбница
- •45. Абсолютная сходимость рядов
- •46. Признаки Дирихле и Абеля
- •47.Функциональные последовательности и ряды.
- •48.Равномерная сходимость функциональных рядов.
- •49.Свойства равном сходящ функции рядов.
- •50.Степенные ряды.
- •53.Ряд Фурье для четн. И нечетн. Ф-ий:
- •54.Ряд Фурье для ф-ций заданных на отрезке .
- •55.Криволинейный интеграл I рода:
- •56.Сведение криволинейного интеграла первого рода к определенному.
- •57.Криволинейный интеграл II рода:
- •59.Случай замкнутого контура:
- •61Cвязьмежду криволинейными интегралами 1-го и 2-го рода
- •62 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •63.Признак полоного диф-ла.
- •64.Вычисление криволинейного интеграла через первообразную
- •65Криволинейный интеграл 2-го рода
- •66 Двойной интеграл
- •67Сведение
- •68 Условие существования
- •69 Основные св-ва 2ного интеграла
- •70Замена переменных в двойном интеграле. Общий случай криволинейных координат
- •71. Формула Грина
- •72. Приложения двойных интегралов.
- •74 Определение и свойства тройного интеграла
- •75 Вычисление тройного интеграла.
- •76 Замена переменных в тройном интеграле.
- •77. Многократные интегралы.
- •80.Вычисление площади поверхности
- •85.Скалярное и векторное поля.
- •88.Циркуляция
- •90.Ротор.
- •92.Интеграл Дирихле.
- •93.Признак Дини сходимости тригонометрического ряда Фурье.
- •94.Признаки Дини, Липшица равномерной сходимости рядов Фурье.
- •96. Комплексная форма тригонометрического ряда Фурье.
- •97.Преобразования Фурье
- •98.Cвойства преобразования Фурье.
55.Криволинейный интеграл I рода:
Криволин.
интегралом 1рода наз-ся предел (если он
существует) интегр. суммы
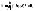 ,при
,при и обознач.
и обознач. =
=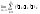 .
Подынтегральная ф-ия
.
Подынтегральная ф-ия наз-ся интегрируемой вдоль кривой
наз-ся интегрируемой вдоль кривой ,
кривая
,
кривая – контуром интегрирования,
– контуром интегрирования, и
и – начальной и конечной точками
интегрирования,
– начальной и конечной точками
интегрирования, – дифференциал дуги.
– дифференциал дуги.
56.Сведение криволинейного интеграла первого рода к определенному.
Предположим, что на кривой К произвольно установлено направление одно из двух возможных так, что положение т.М на кривой может быть определено длиной дуги S=AM отсчитываемой от начальной точки А. Тогда кривую К можно задать параметрически уравнениями вида {x=x(S') y=y(S’)
Где 0≤s≤S. S – Длина кривой К.
Функция
f(x,y) заданная в точке М кривой сводится
к сложной функции f(x(S’),y(S’) переменной
S тогда 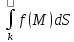 =
=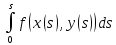 .
.
Предположим,
что кривая К задана произвольными
параметрическими уравнениями

α≤t≤β функции x(t), y(t) непрерывны со своими производными x’, y’ .
В этом случае кривая К спрямляема и если возрастание дуги S=AM соответствует возрастанию параметра t, то
dS=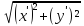 dt
и
dt
и
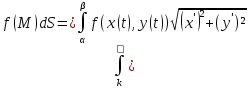
Если
кривая К задана уравнениями в непрямых
координатах, а именно r=r(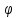 )
)
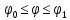
То

57.Криволинейный интеграл II рода:
Криволин.интегралом
2-го рода по кривой
 от ф-ий
от ф-ий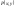 и
и наз-ся предел (если он существует) при
наз-ся предел (если он существует) при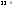 интегральной суммы
интегральной суммы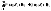 ,и
обозначается
,и
обозначается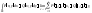 .
Криволинейный интеграл 2-го рода можно
записать в виде
.
Криволинейный интеграл 2-го рода можно
записать в виде
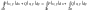 .
.
58Вычисление криволинейного интеграла 2-го рода. Вычисление криволинейного интеграла 2-го рода сводится к вычислению определенного интеграла.
Параметрическое представление кривой интегрирования. Пусть кривая
 задана
параметрическими уравнениями
задана
параметрическими уравнениями ,
, ,
, ,где
,где и
и – непрерывно дифференцированные
функции параметра
– непрерывно дифференцированные
функции параметра ,
причём точке
,
причём точке соответствует
соответствует ,
точке
,
точке – значение
– значение ,
, .
И пусть функции
.
И пусть функции
 и
и
 непрерывны на
непрерывны на
кривой
 .
Тогда криволинейный интеграл 2-го рода
вычисляется по формуле:
.
Тогда криволинейный интеграл 2-го рода
вычисляется по формуле: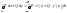 .
.
Явное представление
кривой интегрирования.
Пусть
кривая
 задана уравнением
задана уравнением
 ,
где функции
,
где функции и
и непрерывны на отрезке
непрерывны на отрезке .
Тогда
.
Тогда
криволинейный интеграл 2-го рода вычисляется по формуле:
 .
.
59.Случай замкнутого контура:
Пусть
 – замкнутая криваяНаправл-ие обхода
наз-ся положит, если обл-ть, лежащая
внутри контура остается слева по
отношению к точке, совершающей обход.
Противопол. напр-ие наз-ся отрицат.
Интеграл по замкнутому контуру
– замкнутая криваяНаправл-ие обхода
наз-ся положит, если обл-ть, лежащая
внутри контура остается слева по
отношению к точке, совершающей обход.
Противопол. напр-ие наз-ся отрицат.
Интеграл по замкнутому контуру в положит. напр-ии обозначается:
в положит. напр-ии обозначается: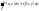
60.Вычисление площади с помощью криволин. Интеграла
Рассм. фигуру Д,ограниченную отрезками PS,QR
прямых параллельные оси Y и двумя кривыми PQ и SR,
 .
.
Рассм. площадь S фигурой,как разность 2-х криволин.
трапеций
 и
и ,получим:
,получим:
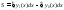 ,
,
с другой стороны:
 .
.
Следов-но площадь:
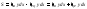
.Если
прибавить сюда
 и
и
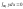 т.к.они
взяты по отрезкам
т.к.они
взяты по отрезкам
параллельно в оси Y,то рав-во не нарушится.
Следов-но:
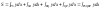 .
.
Если
обозначить контур PSRQP через L,то
.При
правой ориентации осей получим:
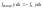 .
.
Для фигуры ограниченной прямолинейными
отрезками PQ,RS параллельным оси X,и
двумя
прямыми

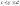 ,с
помощью анологичных
,с
помощью анологичных
рассуждений
получается формула:
 .
.
Таким
образом
 .
.
На практике применяется симметричная формула: