1.Пространство rⁿ

n-мерным координатным пространством наз.множество всевозможных упорядоченных совокупностей (х₁х₂..хn) n действительных чисел х₁х₂..хn это пространство обозначается Rⁿ. Каждая упорядоченная совокупность (х₁х₂..хn) наз. Точкой n-мерного координатного пространства и обознач. М при этом числа х₁х₂..хn наз. координатами точки М запись М(х₁х₂..хn) означает, что точка М имеет координаты х₁х₂..хn . Пусть Rⁿ действительное n-мерное пространство произвольным его точкам 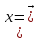=(х₁х₂. 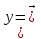х_n) =(у₁у₂.. у_n) поставим в соответствие число(х,у)= х₁ у₁+… х_n у_n,которое наз. скалярным произведением элементов х и у . свойства: 1. (х,у)= (у,х) 2.(х+у)z = (х,z)+ (y,z) 3.(λху)=λ(ху) 4.(х,х)≥0 причем (х,х)=0 только для х=0. Арифметическое значение корня квадратного из скалярного произведения (х,х) наз. нормой элемента х и обознач //х//=√(х,х)

2.Метрическое пространство, евклидово пространство.

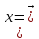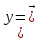пусть Rⁿ действительное n-мерное пространство произвольным его точкам =(х₁х₂. хn)=(у₁у₂.. уn) поставим в соответствие число(х,у)= х₁ у₁+… х_n у_n которое наз. скалярным произведением элементов х и у . n-мерное пространство Rⁿ ,где введено скалярное произведение наз. евклидовым n-мерным пространством. Норма элемента х в евклидовом пространстве Rⁿ опред. по формуле //х//=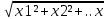n² при n=3 норма элемента х //х//- длина вектора х=(х₁х₂х₃). Нормированное пространство всегда является так называемым метрическим пространством т.е. таким пространством в котором указано правило ставящее в соответствие любым двум элементам х и у действительное число которое наз. расстоянием между этими элементами и обознач. ρ(х,у) указанное правило удовлет. условиям1. ρ(х,у)= ρ(у,х)2. ρ(х,у)<= ρ(х,z)+ ρ(z,у)3. ρ(х,у)>=0 ρ(х,у)=0 == >x=y

3.Основные или важнейшие множества точек пространства

1. множества всевозможных точек пространства Rⁿ координаты которых х₁х₂..хn удовлетворяют неравенству(х₁- х₁⁰)²+…+( хn- хn⁰)²< R² наз. открытым n-мерным шаром радиуса Rс центром в точке М(х₁⁰х₂⁰х₃⁰) 2. Множ. {М} всевозможных точек пространства Rⁿ удовлетворяющих неравенству ρ(М₁М₀)≤ R наз. замкнутым n-мерным шаром радиуса R n-мерным шаром 3. Множ. {М} всевозможных точек пространства Rⁿ координаты которых удовлетвор. равенству ρ(М₁М₀)= R наз. n-мерной сферой радиуса R с центром в точке М₀ 4.открытый n-мерный шар радиуса ε>0 с центром в точке М₀ наз. ε-окрестностью точки М₀ 5. Множ. {М} всевозможных точек пространства Rⁿ координаты которых удовлетворяют неравенствам /х₁- х₁⁰/<d₁…. /хn- хn⁰/<dn, где d₁.. dn-некоторые положительные числа, наз. открытым n-мерным координатным паралелипипедом с центром в точке М₀(х₁⁰х₂⁰…хn⁰) или прямоугольник окрестн. точки М₀ 6.точка М множ. {М} точек пространства Rⁿ наз. внутренней точкой этого множ. если сущ. некоторая ε-окрестность точки М все точки которой принадлежат множ. {М} 7. Точка М пространства Rⁿ наз. внешней точкой множ. {М} если сущ. ε-окрестность точки М все точки которой не принадлежат множ.{М} 8. Точка М пространства Rⁿ наз. граничной точкой множ. {М} если эта точка не является ни внутренней ни внешней точкой этого множ .Граничная точка множ. {М} может как принадлежать так и не принадлежать этому множ. 9. произвольное множ. {М} точек пространства Rⁿ наз. открытым если любая точка этого множ. является внутренней точкой. 10. Произвольное открытое множ. содержащая данную точку М₀ наз. окрестностью точки М₀ 11. произвольное множ. {М} точек пространства Rⁿ наз. замкнутым если это множ. содержит все свои граничные точки 12.{M} точек пр-ва Rⁿ наз.ограниченным, если найдется n-мерный шар содержит все точки этого мн-ва 13.{M} точек пр-ва Rⁿ наз связным, если любые две точки этого мн-ва можно соединить непрерывной кривой все точки которой этому мн-ву 14.Всякое открытое и связное мн-во в пр-ве Rⁿ наз областью 15.Если {M} представляет собой область, то мн-во, полученное присоединением к {M} всех его граничных точек наз замкнутой областью