
- •1.Пространство rⁿ
- •2.Метрическое пространство, евклидово пространство.
- •3.Основные или важнейшие множества точек пространства
- •4.Функции n-переменных.
- •5.Сходимость в пространтсве Rn.
- •6.Предел функции нескольких переменных.
- •8.Повторные пределы.
- •9.Непрерывность функции нескольких переменных.
- •10.Непрерывность функции нескольких
- •11. Основрые свойства непрерывных функций нескольких переменных
- •12. Частные производные ф-ии нескольких переменных
- •13. Дифференцируемость ф-ии нескольких переменных
- •14. Дифференциал функции нескольких переменных
- •15. Достаточное условие дифференцируемости ф-ии нескольких переменных
- •16. Дифференцирование сложной ф-ии
- •17. Однородная функция. Теорема эйлера об однородных функциях
- •18. Инвариантность формы первого дифференциала функции нескольких переменных
- •19. Геометрический смысл дифференциуемости функции двух переменных
- •20. Производная по направлению
- •21.Частные производные высшего порядка.
- •22.Теорема о равенстве смешанных производных второго порядка ф-ции двух переменных.
- •23.Производные высших порядков.
- •26. Экстремум функции многих переменных.
- •27.Достаточные услов локальн экстрем ф-ций нескол перемен.
- •28. Критерий Сильвестра
- •29.Определение наибольшего и наименьшего значения
- •30.Не явные ф-ции.
- •31.Теорема о существ и диф-ти неявной ф-ции.
- •32.Вычисление частных производн неявно заданных ф-ций.
- •33.Неявные ф-ции определ систем функцион уравнений.
- •34. Зависимость ф-и нескольких переменных
- •35.Функциональные матрици
- •36. Усл.Экстремум
- •37.Метод неопредёлённых множетелей Логранжа.
- •38.Числовой ряд. Сходимость, расходимость рядов.
- •39.Необход признак сходим ряда.
- •40. Признак сравнения рядов
- •41.Признак Даламбера.
- •42.Признак Коши.
- •43. Интегральный признак Коши
- •44. Признак Лейбница
- •45. Абсолютная сходимость рядов
- •46. Признаки Дирихле и Абеля
- •47.Функциональные последовательности и ряды.
- •48.Равномерная сходимость функциональных рядов.
- •49.Свойства равном сходящ функции рядов.
- •50.Степенные ряды.
- •53.Ряд Фурье для четн. И нечетн. Ф-ий:
- •54.Ряд Фурье для ф-ций заданных на отрезке .
- •55.Криволинейный интеграл I рода:
- •56.Сведение криволинейного интеграла первого рода к определенному.
- •57.Криволинейный интеграл II рода:
- •59.Случай замкнутого контура:
- •61Cвязьмежду криволинейными интегралами 1-го и 2-го рода
- •62 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •63.Признак полоного диф-ла.
- •64.Вычисление криволинейного интеграла через первообразную
- •65Криволинейный интеграл 2-го рода
- •66 Двойной интеграл
- •67Сведение
- •68 Условие существования
- •69 Основные св-ва 2ного интеграла
- •70Замена переменных в двойном интеграле. Общий случай криволинейных координат
- •71. Формула Грина
- •72. Приложения двойных интегралов.
- •74 Определение и свойства тройного интеграла
- •75 Вычисление тройного интеграла.
- •76 Замена переменных в тройном интеграле.
- •77. Многократные интегралы.
- •80.Вычисление площади поверхности
- •85.Скалярное и векторное поля.
- •88.Циркуляция
- •90.Ротор.
- •92.Интеграл Дирихле.
- •93.Признак Дини сходимости тригонометрического ряда Фурье.
- •94.Признаки Дини, Липшица равномерной сходимости рядов Фурье.
- •96. Комплексная форма тригонометрического ряда Фурье.
- •97.Преобразования Фурье
- •98.Cвойства преобразования Фурье.
50.Степенные ряды.
Опред:
степенным рядом наз функционал ряд
вида: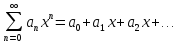 где
где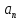 -
действ числа, которые наз каэф ряда
степен рядом так же ряд: :
-
действ числа, которые наз каэф ряда
степен рядом так же ряд: :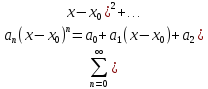 Теор Абеля:если степенн ряд
Теор Абеля:если степенн ряд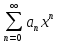 сходит при некотор знач
сходит при некотор знач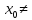 0
то он абсал сход при любом х для которого
0
то он абсал сход при любом х для которого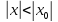 Д-во: по услов ряд
Д-во: по услов ряд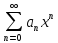 - сходит поэтому по необход признаку
сходим:
- сходит поэтому по необход признаку
сходим: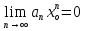 ,
поэтому существ число C>0 что для всех
n выполн нерав :
,
поэтому существ число C>0 что для всех
n выполн нерав :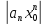 <c;
<c; n<c
n<c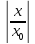 n
ряд
n
ряд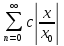 n
– сходит при
n
– сходит при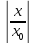 <1
поэтом абсал сход и данный ряд при
обсал велич
<1
поэтом абсал сход и данный ряд при
обсал велич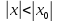 .
Следствие: если степен ряд
.
Следствие: если степен ряд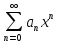 рассход при х1 то он расход и при любом
х для котор
рассход при х1 то он расход и при любом
х для котор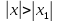 Из теор Абеля след что если степен ряд
сход при
Из теор Абеля след что если степен ряд
сход при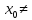 0
то он сход при
0
то он сход при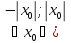 если он расход при х=х1 то он расход при
x<
если он расход при х=х1 то он расход при
x<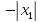 ;
x>
;
x>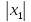 .
Определ: радиусом сходим степен ряда
.
Определ: радиусом сходим степен ряда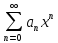 наз число R токое что при
наз число R токое что при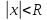 ряд сход, а при
ряд сход, а при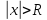 ряд расход. Интервалом сходим ряда
ряд расход. Интервалом сходим ряда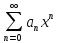 наз интервал (-R;R) где R- радиус сходим
ряда; если степен ряд
наз интервал (-R;R) где R- радиус сходим
ряда; если степен ряд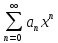 сход в единств точке то считает R=0, если
он сход при любом х, то полог R=
сход в единств точке то считает R=0, если
он сход при любом х, то полог R=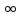 .
Найд выраж радиуса сходим степен ряда
через его каэф для этого примен признак
Даламбера к исслед сходим ряда:
.
Найд выраж радиуса сходим степен ряда
через его каэф для этого примен признак
Даламбера к исслед сходим ряда: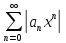 предпол
что an
предпол
что an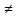 0
0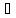
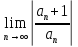 =
=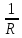 ,
тогда
,
тогда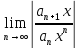 =
=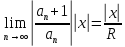 ряд сходится при
ряд сходится при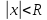 и расход при
и расход при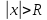 ,
тоесть R-радиус сходим т.о. радиус сходим
степенного ряда определ выраж:R=
,
тоесть R-радиус сходим т.о. радиус сходим
степенного ряда определ выраж:R=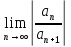 ,
если этот придел сущ. Предпол что сущ
,
если этот придел сущ. Предпол что сущ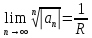 применяя признак Коши получ:
применяя признак Коши получ: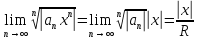 ряд сход если
ряд сход если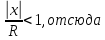
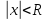 следов радиус сход: R=
следов радиус сход: R=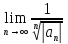 .
Свойств степенных рядов:1) степен ряд
.
Свойств степенных рядов:1) степен ряд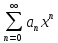 сходит равном на отрезке
сходит равном на отрезке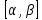 целиком принадл его интервалу сходим;
2) сумма степен ряда явл непрер ф-цией
на любом отрезке целиком пренадл его
интервалу сходим; 3) степен ряд можно
почленно интегрир по любому отрезку
целик пренадл его интервалу сходим; 4)
если степен ряд
целиком принадл его интервалу сходим;
2) сумма степен ряда явл непрер ф-цией
на любом отрезке целиком пренадл его
интервалу сходим; 3) степен ряд можно
почленно интегрир по любому отрезку
целик пренадл его интервалу сходим; 4)
если степен ряд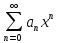 имеет интерв (-R;R) и S(x) его сумма то ряд
имеет интерв (-R;R) и S(x) его сумма то ряд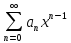 получен почлен дифференц исходного
ряда имеет тот же интерв сход при чем
любое х
получен почлен дифференц исходного
ряда имеет тот же интерв сход при чем
любое х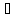 (-R;R):
S’(x)=
(-R;R):
S’(x)=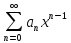 ;
5) степен ряд можно почлен диференц
любое число раз в интерв его сходим.
Разлож некотор ф-ций в степен ряды:
рассм ряд
;
5) степен ряд можно почлен диференц
любое число раз в интерв его сходим.
Разлож некотор ф-ций в степен ряды:
рассм ряд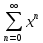 =1+х+х2+…
этот ряд явл геом прогресс и сход при
-1<x<1 сумма: S(x)=
=1+х+х2+…
этот ряд явл геом прогресс и сход при
-1<x<1 сумма: S(x)=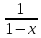 эта ф-ла представл собой разлож в степен
ряд ф-ции: f(x)=
эта ф-ла представл собой разлож в степен
ряд ф-ции: f(x)=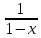 радиус сход R=1. Если вместо х подстав
–ч то получ разлож в степн ряд
ф-уи:f(x)=1-x+x2-x3…
радиус сход R=1. Если вместо х подстав
–ч то получ разлож в степн ряд
ф-уи:f(x)=1-x+x2-x3…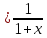 интерг этот ряд по отр:
интерг этот ряд по отр: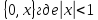 получ:
получ: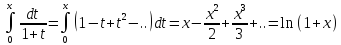 ,
при х=1 этот ряд сход т.к. ln(1+1)=ln2=1-
,
при х=1 этот ряд сход т.к. ln(1+1)=ln2=1-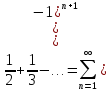 при замене х на –х получ: ln(1-x)=-x-
при замене х на –х получ: ln(1-x)=-x-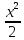 -
-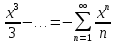 ряд сход при
ряд сход при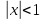 .
.
51.Ряд Тейлора:
Пусть
ф-ия
 имеет в окр-ти точки
имеет в окр-ти точки производные любого порядка. Ряд
производные любого порядка. Ряд
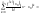
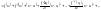 Наз-ся
рядом Тейлора ф-ии
Наз-ся
рядом Тейлора ф-ии
 в точке
в точке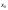 .Если
.Если ,
то ряд Тейлора имеет вид
,
то ряд Тейлора имеет вид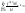
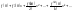 и
наз-ся рядом Маклорена.
и
наз-ся рядом Маклорена.
52. Тригонометрический ряд Фурье:
Пусть
( )
– ортогональная система функций в
)
– ортогональная система функций в .Выр-ие
.Выр-ие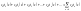 .
Наз-ся обобщенным рядом Фурье по
ортогональной системе ф-ий (
.
Наз-ся обобщенным рядом Фурье по
ортогональной системе ф-ий ( ).
Если (
).
Если ( )
– основная тригоном-ая система ф-ий,
то ряд наз-ся тригоном.рядом Фурье.
)
– основная тригоном-ая система ф-ий,
то ряд наз-ся тригоном.рядом Фурье.
53.Ряд Фурье для четн. И нечетн. Ф-ий:
Четн.
ф-ия:
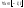 .Коэф-ты
ряда Фурье
.Коэф-ты
ряда Фурье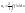 ,
,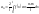 ,
, ,
,
 ,а
сам ряд Фурье
,а
сам ряд Фурье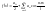 .Нечетн.ф-ия:
.Нечетн.ф-ия: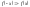
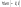 .Коэф-ты
ряда Фурье
.Коэф-ты
ряда Фурье ,
,
 ,
,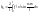 ,
,

 ,а
сам ряд Фурье
,а
сам ряд Фурье
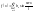
54.Ряд Фурье для ф-ций заданных на отрезке .
Расмотр
f(x) определенную и кусочно-диференцируемую
на
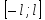 .
Введем новую переменную: t=
.
Введем новую переменную: t=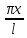 ,
тогда x=
,
тогда x=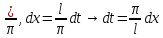 .
Если x
.
Если x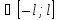 то t
то t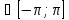 и тогда получаем ф-цию: f(x)=f(
и тогда получаем ф-цию: f(x)=f(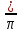 )=
)=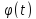 для этой ф-ции в точках непрерывности
для этой ф-ции в точках непрерывности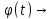
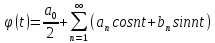 ,
где an=
,
где an=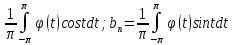 ;
возращаясь к перемен х получим:
f(x)=
;
возращаясь к перемен х получим:
f(x)=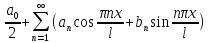 (*);
где каэф an; bn определ по формулам:
an=
(*);
где каэф an; bn определ по формулам:
an=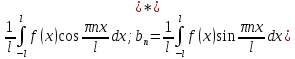 .
То есть для ф-ции заданной нан отрезке
.
То есть для ф-ции заданной нан отрезке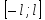 разложение в ряд Фурье имеет вид (*) с
каэф определяемыми выражение (**).
разложение в ряд Фурье имеет вид (*) с
каэф определяемыми выражение (**).
