
- •Динамика
- •1. Введение в динамику. Законы динамики.
- •Импульс силы
- •4. Относительное движение материальной точки.
- •Здесь – абсолютное ускорение точки по отношению к о.С.О. По теореме Кориолиса
- •8. Принцип Германа-Эйлера-д'Аламбера.
- •Динамики
- •Прямолинейные колебания материальной точки. Некоторые виды колебаний.
- •На материальную точку действуют и
- •Проанализируем амплитуду вынужденных колебаний:
Прямолинейные колебания материальной точки. Некоторые виды колебаний.
Существуют в природе силы, которые всегда стремятся вернуть тело в положение равновесия. Такие силы называются восстанавливающими. Модуль этих сил зависит от величины смещения тела от равнoвecного положения, а направлены они всегда в сторону равновесного состояния. Под действием таких сил тело может совершать колебательные движения.
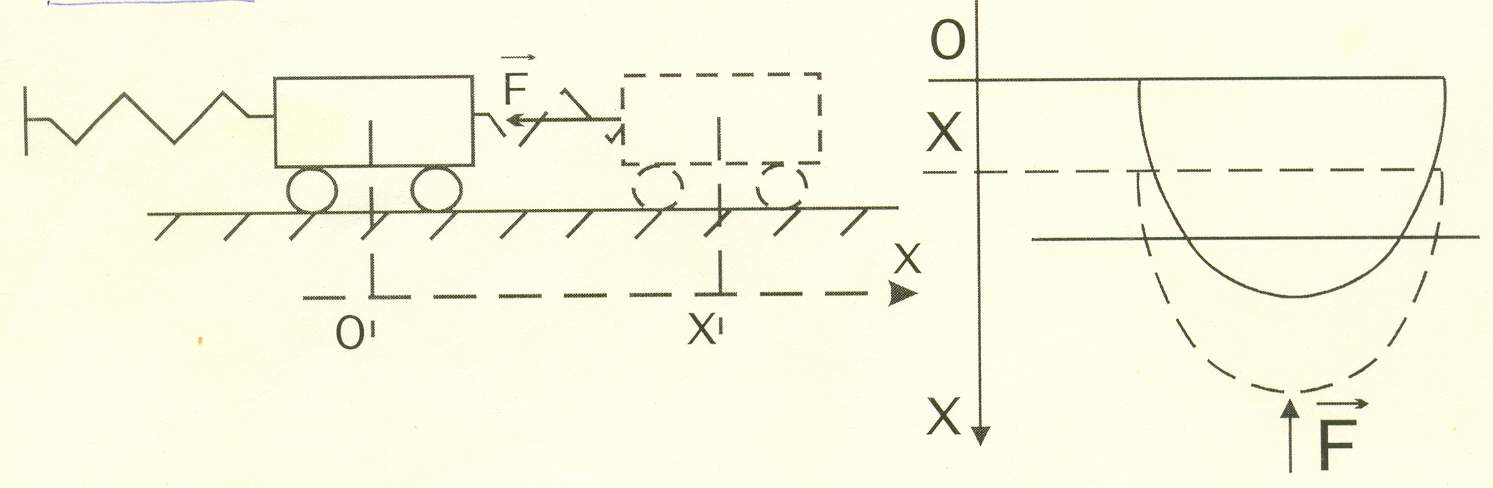
Например:
![]() –
восстанавливающая сила
–
восстанавливающая сила
![]() –
восстанавливающая сила (архимедова)
изменение весового водоизменения
–
восстанавливающая сила (архимедова)
изменение весового водоизменения
Кроме
восстанавливающих сил на тела могут
действовать другие внешние силы
![]() и
силы сопротивления
и
силы сопротивления
![]() .
.
Вид колебательного движения тела зависит от того, какие из этих сил на него действуют и их соотношения.
Мы
рассмотрим случаи простейшие: колебания
прямолинейные, когда
![]() – восстанавливающая сила,
– восстанавливающая сила,
![]() –
сила сопротивления,
–
сила сопротивления,
![]() – возмущающая сила.
– возмущающая сила.
Действует только
Дифференциальное уравнение движения:
![]() – свободные
колебания.
– свободные
колебания.
Действуют силы: и
Дифференциальное уравнение движения:
![]() – свободные
колебания при вязком сопротивлении.
– свободные
колебания при вязком сопротивлении.
Действуют силы: и
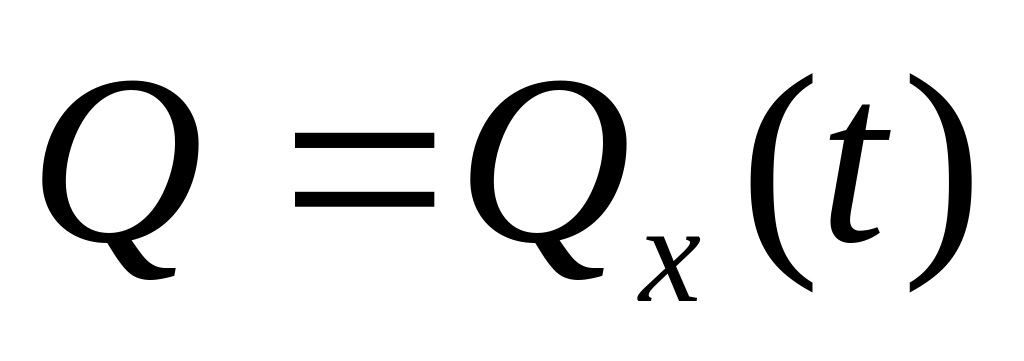
Дифференциальное уравнение движения:
![]() – вынужденные колебания.
– вынужденные колебания.
4. Действуют силы: ; ; .
Дифференциальное уравнение движения:
![]() –
вынужденные
колебания при вязком сопротивлении.
–
вынужденные
колебания при вязком сопротивлении.
Явление колебаний (колебательные процессы) имеет место во многих отраслях: радиотехника, акустика и т.д. Природа этих колебаний различна, но законы у них одинаковы, значение изучения колебаний выходит за рамки этого курса.
В механике возможны непрямолинейные колебания точки, колебания тел и системы тел. Для всех случаев изменятся параметры характеризующие движение и их число, а дифференциальные уравнения будут такого же вида.
Свободные колебания.
На материальную точку действует только восстанавливающая сила , где
с – коэффициент пропорциональности (жесткости).
Дифференциальное уравнение движения:
![]()
Обозначим
![]() ,
тогда
,
тогда ![]() (А)
(А)
Т.о. дифференциальное уравнение движения в этом случае является линейным, однородным, второго порядка с постоянными коэффициентами. Характеристическое уравнение этого дифференциального уравнения:
![]() ,
а корни
,
а корни
![]() – числа
мнимые, тогда общее решение уравнения
(А) будет:
– числа
мнимые, тогда общее решение уравнения
(А) будет:
![]() (А/)
(А/)
здесь А1 и А2 – постоянные интегрирования.
Чтобы проще представить движение заменим постоянные
![]() ,
тогда
,
тогда
![]() или
или
![]() (А//)
(А//)
Здесь
постоянными интегрирования являются
и
![]() , которые определяются из граничных
условий – начальным положением точки
, которые определяются из граничных
условий – начальным положением точки
![]() и
её начальной скоростью
и
её начальной скоростью
![]() .
Уравнение
(А//)
показывает, что под действием только
восстанавливающей силы материальная_точка
совершает гармонические колебания.
Такие колебания называются свободными.
.
Уравнение
(А//)
показывает, что под действием только
восстанавливающей силы материальная_точка
совершает гармонические колебания.
Такие колебания называются свободными.
Величина
"k" называется частотой (угловой,
круговой, циклической). Определяет
число колебаний совершаемых точкой за
промежуток времени
![]() сек. "k" зависит от свойств системы
(m и с) и называется собственной частотой.
сек. "k" зависит от свойств системы
(m и с) и называется собственной частотой.
Наибольшее
отклонение от положения равновесия
называется амплитудой (А), аргумент
![]() – фаза,
– начальная фаза.
– фаза,
– начальная фаза.
Определим
постоянные
и
из начальных условий
![]()
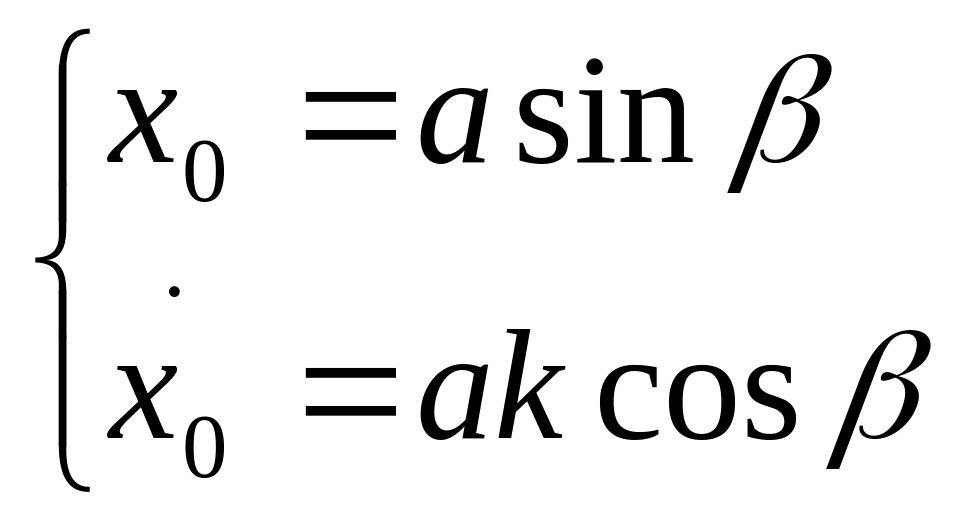
Решение этой системы даст
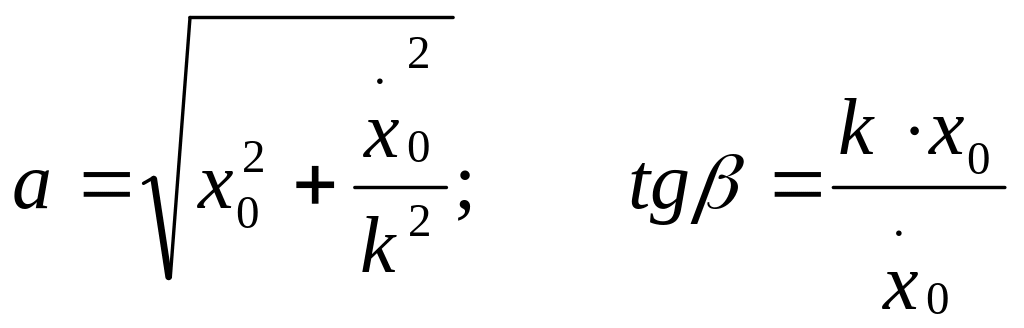
Графически зависимость (А//) можно показать:
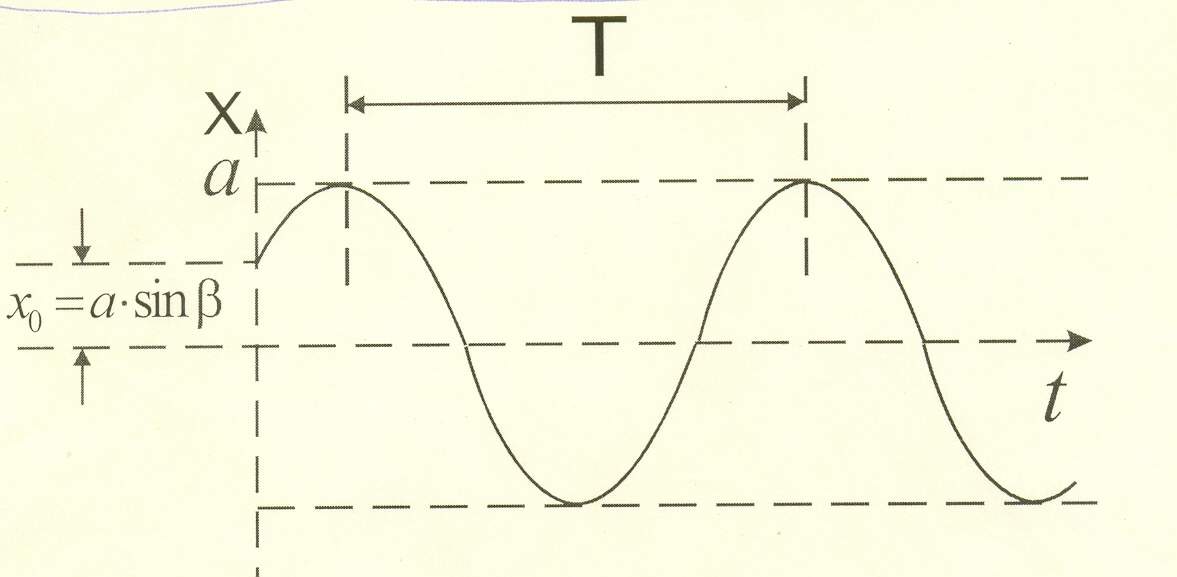
График показывает, что свободные колебания – периодичны. За период (Т) совершается полный цикл движения. Определим Т:
![]()
![]() ,
откуда
,
откуда
![]() ,
, ![]()
Период Т, как и частота k не зависят от граничных условий, а являются характеристиками системы, зависят от её параметров m и с.
Т увеличивается с увеличением массы m и уменьшением k коэффициента пропорциональности.
Определим
влияние постоянной сила
![]() на
свободные колебания
на
свободные колебания
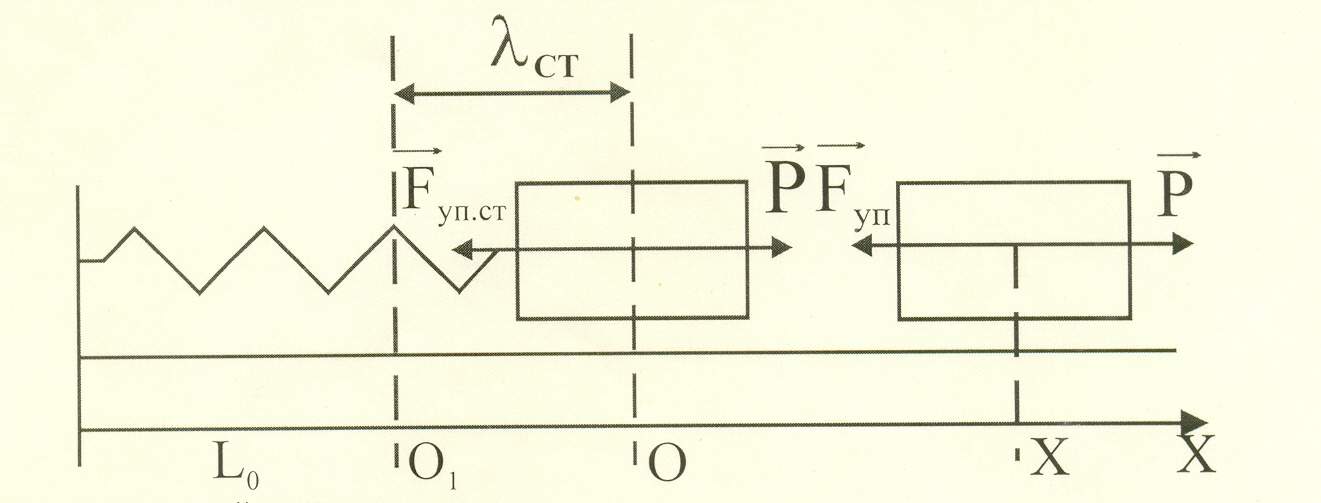
материальной точки.
Дифференциальное уравнение движения:
![]() ,
где
,
где
![]()
тогда
![]() ,
или
,
или
Получим дифференциальное уравнение движения, аналогичное (А).
Т.о.
постоянная по модулю и направлению
сила не изменяет характера движения
материальной точки под действием
восстанавливающей силы
.
Изменяется
только центр колебаний (![]() ).
).
Свободные колебания при наличии вязкого сопротивления.
