2.2. Частотные характеристики

Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой и частотой , то после затухания переходных процессов на выходе также возникают синусоидальные колебанияc той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как известно из курса “Основы теории цепей, часть 1”, синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать каки

Подавая на вход системы гармонические колебания с постоянной амплитудой, но различными частотами, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний.

Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний:

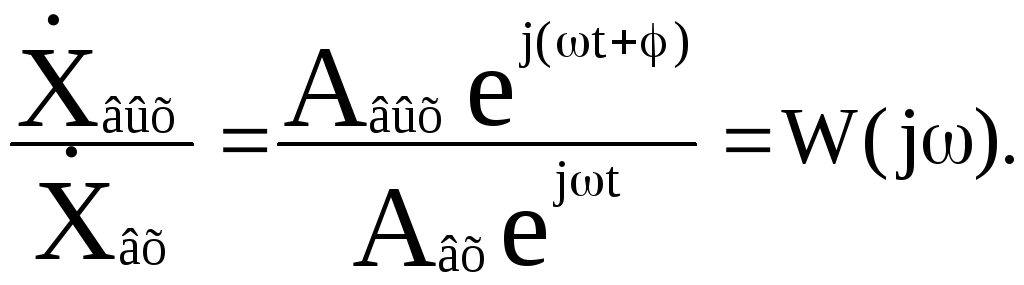(2.6)

Функция называетсякомплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную j:

(2.7)

В различных формах записи функцию можно представить в следующем виде:

(2.8)

где и- действительная и мнимая части комплексной частотной функции,

и - модуль и аргумент комплексной частотной функции.

При фиксированном значении частоты комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.7.

+j

+1

Рис.2.7

Изменение частоты приведет к изменению величины и расположения вектора на комплексной плоскости, а конец вектора опишет некоторую траекторию. Геометрическое место концов векторов комплексной частотной функции при изменении частоты от нуля до бесконечности называется амплитудно-фазовой частотной характеристикой (АФЧХ).

В свою очередь все величины, представленные в (2.8), являются соответствующими частотными функциями, а построенные по выражениям для функций графики - частотными характеристиками.

называется вещественной частотной, а -мнимой частотной характеристикой.

показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.

показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.

Между всеми частотными характеристиками существует непосредственная связь, вытекающая из тригонометрических соотношений и поясняемая рис.2.7.

В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ.

Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности на выходе к мощности на входев технике принят бел. Так как мощность сигнала пропорциональна квадрату его амплитуды, получим:

Но так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее принят децибел 1дБ=0,1 Б.

С учетом этого можно записать:

Величина логарифма амплитудной частотной характеристики, выраженная в децибелах

называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ).

Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз - на 40 дБ, в 1000 раз - на 60 дБ и т.д.

Вычислим, какому отношению амплитуд соответствует один децибел, два и т.д.

То есть 1 дБ 1,122.

2 дБ (1,122)²=1,259;

3 дБ (1,122)³=1,412;

4 дБ 1,585;

5 дБ 1,778;

6 дБ 1,995 2.

Фазовая частотная характеристика , построенная в полулогарифмическом масштабе (в координатах: угол в градусах или радианах и ), называетсялогарифмической фазовой частотной характеристикой (ЛФЧХ).

За единицу измерения частоты используется логарифмическая единица декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.

В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную

ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно взять в точке , так как. Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.

Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза . Ось абсцисс соответствует значению, то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).

Из рассмотренных здесь частотных характеристик две можно получить экспериментально-амплитудную и фазовую. Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например- по формуле (2.8). Кроме того, рассчитав по экспериментальным данным, по (2.7) путем обратной подстановки (заменив j на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).