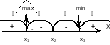Тема 2.3. Приложение производной к исследованию функции. Промежутки монотонности функции

Функция называется возрастающей в некотором промежутке, если в этом промежутке большему значению аргумента соответствует большее значение функции, т.е. если х₂ > х₁, то f(x₂) > f(x₁).

Функция называется убывающей в некотором промежутке, если в этом промежутке большему значению аргумента соответствует меньшее значение функции, т.е. если х₂ > х₁, то f(x₂) < f(x₁).

Промежутки, в которых функция возрастает или убывает, называются промежутками монотонности.

Признак возрастания и убывания функции

Возрастание и убывание функции y = f(x) характеризуется знаком ее первой производной: если в некотором промежутке первая производная больше нуля, то функция возрастает, а если первая производная меньше нуля, то функция убывает в этом промежутке.

КРАТКО:

если f ’(x) > 0, то f(x) 

f ’(x) < 0, то f(x) 

Критическими точками функции называются внутренние точки области определения (значения аргумента), при которых производная обращается в нуль или не существует (терпит разрыв).

ПРАВИЛО НАХОЖДЕНИЯ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ

№

Краткая запись

1

Определить область определения функции

D(y)

2

Найти первую производную

y’ = f’(x)

3

Найти критические точки (нули и точки разрыва функции) первой производной, (для этого первую производную приравнять к нулю)

f ’(x) = 0 

х₁, х₂, х₃ – критические точки

4

Нанести критические точки на область определения функции (ось ОХ)

5

Исследовать знак первой производной в каждом из полученных промежутков (для этого взять любой х внутри рассматриваемого промежут-ка и подставить в первую производную)

если f ’(x) > 0  f(x) 

f ’(x) < 0  f(x) 

на рассматриваемом промежутке

6

Записать ответ

Ответ:

f(x)  при х  (-; х₁) , (х₃; + )

f(x)  при х  (х₁; х₃)

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

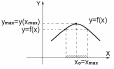
Точка х₀ называется точкой максимума функции y = f(x), если значение функции f(x) в точке х₀ больше, чем ее значения во всех точках некоторого интервала, содержащего точку х₀, т.е выполняется неравенство:

f(x₀)  f(x) при х₀ = х_max

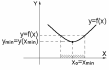
Точка х₀ называется точкой минимума функции y = f(x), если значение функции f(x) в точке х₀ меньше, чем ее значения во всех точках некоторого интервала, содержащего точку х₀, т.е выполняется неравенство:

f(x₀)  f(x) при х₀ = х_max

Х₀ – точка максимума, если f(x₀)  f(x)

для всех х из окрестности х₀

Х₀ – точка минимума,

если f(x₀)  f(x)

для всех х из окрестности х₀

Точки экстремума –

это точки минимума и максимума

(абсциссы точек)

Максимум функции –

это значение (у) функции y = f(x) в точке максимум. y_max = y(x_max)

Минимум функции –

это значение (у) функции y = f(x) в точке минимум. y_min = y(x_min)

Экстремум функции –

это минимум и максимум функции (ординаты точек)

Точками экстремума могут служить только критические точки, т.е. точки, принадлежащие области определения функции, в которых производная f’(x) обращается в нуль или терпит разрыв

Достаточный признак экстремума

Если при переходе через критическую точку х₀ производная f’(x) меняет знак, то функция f(x) имеет в точке х₀ экстремум: МИНИМУМ в том случае, когда первая производная меняет знак с минуса на плюс, и МАКСИМУМ – когда с плюса на минус. Если же при переходе через критическую точку х₀ производная f’(x) не меняет знак, то функция f(x) в точке х₀ не имеет экстремума.

КРАТКО:

если через х₀ – критическую точку f ’(x) меняет знак с « + » на « - », то х₀ = х_max

с « - » на « + », то х₀ = х_min

ПРАВИЛО НАХОЖДЕНИЯ ЭКСТРЕМУМОВ ФУНКЦИИ С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ

№

Этапы

Краткая запись

1

Определить область определения функции

D(f)

2

Найти первую производную

f’(x)

3

Найти критические точки функции y = f(x), т.е. точки, в которых производная равна нулю или не существует

f’(x) = 0 

х₁, х₂, х₃ – критические точки

4

Нанести критические точки на область определения функции (ось ОХ)

5

Определить знак первой производной в промежутках (для этого взять любое число внутри промежутка и подставить в уравнение первой производной)

если f ’(x) > 0  f(x) 

f ’(x) < 0  f(x) 

на рассматриваемом промежутке

6

Из критических точек определить точки экстремума функции

если через х₀ - критическую точку f’(x) меняет знак

с « + » на « - », то х₀ = х_max

с « - » на « + », то х₀ = х_min

7

Найти значение функции в точках экстремума. Для этого подставить точки минимума и максимума в первоначальную функцию, т.е y = f(x)

х₁ – точка max  f_max = f(x₁)

х₃ – точка min  f_min = f(x₃)

8

Записать результат исследования функции, т.е. ответ

Ответ: f_max = f(x₁) = A;

f_min = f(x₃) = B,

где А, В = const