РАЗДЕЛ 3. ОСНОВЫ ТЕОРИИ КОМПЛЕКСНЫХ ЧИСЕЛ, ТЕОРИИ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ДИСКРЕТНОЙ МАТЕМАТИКИ.

Тема 3.1. Основы теории комплексных чисел.

План:

Пункт 1. Понятие комплексного числа.

Пункт 2. Геометрическая интерпретация комплексного числа.

Пункт 3. Арифметические действия над комплексными числами.

Пункт 4. Понятие модуля и аргумента комплексного числа.

Пункт 5. Действия над комплексными числами в тригонометрической форме.

Пункт 6. Показательная форма записи комплексного числа.

Пункт 1. Понятие комплексного числа.

Существует элемент i (мнимая единица) такой, что i² = – 1.

Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b ≠ 0) называют чисто мнимыми.

Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

Для любого комплексного числа существует комплексное число, противоположное данному. Оно обозначается - z = -a - bi.

Для любого комплексного числа существует сопряженное комплексное число, которое отличается от данного противоположным знаком перед мнимой частью. Такое число обозначается z = a – bi.

Свойства сопряженных комплексных чисел:

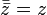• (сопряжённое к сопряжённому есть исходное).

• 

• 

• 

• 

• 

Запись комплексного числа z = a + bi называется алгебраической формой записи комплексного числа.

Перейдем теперь к вопросу о решении полного квадратного уравнения. Квадратным уравнением называют уравнение вида: ax² + bx + c = 0, где x – неизвестная, a, b, c – действительные числа, соответственно первый, второй коэффициенты и свободный член, причем a ≠ 0. Решим это уравнение, выполнив над ним ряд несложных преобразований.

Разделим все члены уравнения на a ≠ 0 и перенесем свободный член в правую часть уравнения: 

К обеим частям уравнения прибавим выражение   с тем, чтобы левая его часть представляла полный квадрат суммы двух слагаемых:

Извлечем корень квадратный из обеих частей уравнения: 

Найдем значения неизвестной: 

Теперь можно исследовать полученное решение. Оно зависит от значения подкоренного выражения, называемого дискриминантом квадратного уравнения. Если  b2 – 4ac > 0, то есть действительное число и квадратное уравнение имеет действительные корни. Если же – мнимое число, квадратное уравнение имеет мнимые корни.

Результаты исследования представлены ниже в таблице:

Итак, введение комплексных чисел позволяет разработать полную теорию квадратных уравнений. В поле комплексных чисел разрешимо любое квадратное уравнение.

Примеры.

1. Решите уравнение x² – 2x – 8 = 0.

Решение. Найдем дискриминант  D = b² – 4ac = (– 2)2 – 4•1•(– 8) = 36 > 0.

Уравнение имеет два действительных корня: 

2. Решите уравнение x² + 6x + 9 = 0.

Решение. D = 62 – 4•1•9 = 0, уравнение имеет два равных действительных корня:

3. Решите уравнение x² – 4x + 5 = 0.

Решение. D = 16 – 4•1•5 = – 4 < 0, уравнение имеет мнимые корни:  

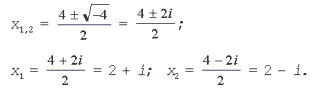
Пункт 2. Геометрическая интерпретация комплексного числа.

Известно, что отрицательные числа были введены в связи с решением линейных уравнений с одной переменной. В конкретных задачах отрицательный ответ истолковывался как значение направленной величины (положительные и отрицательные температуры, передвижения в противоположных направлениях, прибыль и долг и т.п.). Однако еще в ХVI веке многие математики не признавали отрицательных чисел. Только с введением координатной прямой и координатной плоскости отчетливо п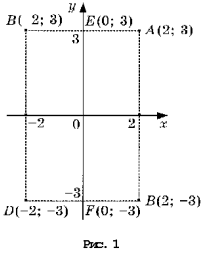 роявился смысл отрицательных чисел, и они стали такими же «равноправными» и понятными, как и натуральные числа. Аналогично обстоит дело с комплексными числами. Смысл их отчетливо проявляется при введении их геометрической интерпретации.

Г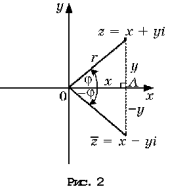 еометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.

На рисунке 1 изображена координатная плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3).

Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости.

Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi, где y ≠ 0 – точки оси ординат. Поэтому ось Oy называют мнимой осью, а ось Ox – действительной осью.

Сопряженным комплексным числам соответствуют точки, симметричные относительно оси абсцисс (рис. 2).

Противоположным комплексным числам z = a + bi и - z = -a – bi соответствуют точки, симметричные относительно начала координат.

Пункт 3. Арифметические действия над комплексными числами.

Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c + di, то a = c, b = d и, обратно, если a = c, b = d, то a + bi = c + di.

Правило сложения и вычитания комплексных чисел. При сложении двух комплексных чисел надо сложить соответственно их действительные и мнимые части, т.е. (a + bi) ± (c + di) = (a ± c) + (b ± d)i.

Примеры:

4. (2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i;

5. (– 2 + 3i) + (1 – 8i) = (– 2 + 1) + (3 + (– 8))i = – 1 – 5i;

6. (– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3 + (– 3))i =

= – 1 + 0i = – 1.

7. (5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i;

8. (3 – 2i) – (1 – 2i) = (3 – 1) + ((– 2) – (– 2))i = 2 + 0i = 2.

Правило умножения комплексных чисел. Умножение двух комплексных чисел производится по формуле: (a + bi)(c + di) = (aс + bd) + (ad + bc)i.

Докажем эту формулу: (a + bi)(c + di) = ac + adi + bdi² = (ac – bd) + (ad + bc)i.

Примеры:

9. (– 1 + 3i)(2 + 5i) = – 2 – 5i + 6i + 15i² = – 2 – 5i + 6i – 15 = – 17 + i; 

10. (2 + 3i)(2 – 3i) = 4 – 6i + 6i – 9i2 = 4 + 9 = 13.

Из примеров следует, что результатом сложения, вычитания, произведения двух комплексных чисел может быть число действительное. В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части, т.е. (a + bi)(a – bi) = a² + b².

Действительно: (a + bi)(a – bi) = a² – abi + abi – b²i² = a² + b².

Произведение двух чисто мнимых чисел – действительное число.

Например:  5i•3i = 15i² = – 15; – 2i•3i = – 6i² = 6,  и вообще   bi•di = bdi² = – bd.

Правило деления. Деление комплексного числа a + bi на комплексное число c + di ≠ 0 определяется как операция обратная умножению и выполняется по формуле:

.

Формула теряет смысл, если c + di = 0, так как тогда c² + d² = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.

Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.

Пример 11:

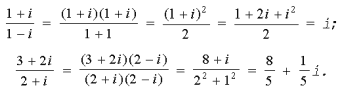
Пункт 4. Понятие модуля и аргумента комплексного числа.

Т очка координатной плоскости, соответствующая комплексному числу z = x + yi, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла φ между положительной полуосью Ox и лучом Oz (рис. 3).

Расстояние r от начала системы координат до точки, соответствующей комплексному числу z, называют модулем этого числа. Тогда по теореме Пифагора (рис. 2) имеем:   r² = x² + y² = (x + yi)(x – yi) = z•z.

Отсюда найдем модуль комплексного числа как арифметическое (неотрицательное) значение корня:

Если комплексное число z изображается точкой оси абсцисс (т.е. является действительным числом), то его модуль совпадает с абсолютным значением. Все комплексные числа, имеющие модуль 1, изображаются точками единичной окружности – окружности с центром в начале системы координат, радиуса 1 (рис. 4).

У гол φ между положительной полуосью Ox и лучом Oz называют аргументом комплексного числа z = x + yi (рис. 3).

Сопряженные комплексные числа имеют один и тот же модуль   и аргументы, отличающиеся знаком: φ = – φ.

В отличие от модуля аргумент комплексного числа определяется неоднозначно. Аргумент одного и того же комплексного числа может иметь бесконечно много значений, отличающихся друг от друга на число, кратное 360°. Например, число z (рис. 3) имеет модуль r, аргумент же этого числа может принимать значения φ; φ + 360°; φ + 720°; φ + 1080°; … или значения φ – 360°; φ –720°; φ – 1080°; … Данное значение модуля r и любое из приведенных выше значений аргумента определяют одну и ту же точку плоскости, соответствующую числу z.

Пусть точке с координатами (a; b) соответствует комплексное число z = a + bi. Запишем это комплексное число через его модуль и аргумент. Воспользуемся определением тригонометрических функций синуса и косинуса (рис. 3): a = r cos φ; b = r sin φ. Тогда число z выражается через модуль и аргумент следующим образом:  z = a + bi = r(cos φ + i sin φ).

Выражение z = r(cos φ + i sin φ) называют тригонометрической формой комплексного числа, в отличии от выражения z=a+bi, называемого алгебраической формой комплексного числа.

Приведем примеры обращения комплексных чисел из алгебраической формы в тригонометрическую:

Пример 12.

а) Для числа i имеем r = 1, φ = 90°, поэтому   i = 1(cos 90° + i sin 90°);

б) Для числа – 1 имеем r = 1, φ = 180°, поэтому  – 1 = 1(cos 180° + i sin 180°);

в) Для числа 1 + i имеем поэтому

г) Для числа имеем r = 1, φ = 45°, поэтому

д) Для числа имеем r = 2, φ = 120°, поэтому 

Справедливость приведенных равенств нетрудно проверить путем подстановки в их правой части числовых значений тригонометрических функций.

Итак, для того, чтобы комплексное число, заданное в алгебраической форме, обратить в тригонометрическую форму, необходимо найти его модуль r и аргумент φ, пользуясь формулами:

   

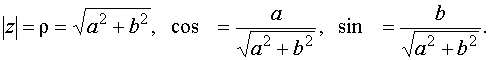
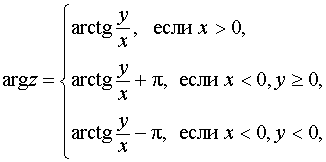
Пункт 5. Действия над комплексными числами в тригонометрической форме.

Условие равенства комплексных чисел, записанных в тригонометрической форме, состоит в том, что модули их равны, а аргументы могут отличаться на слагаемое, кратное 2π, то есть r₁ = r₂ и φ₁ = φ₂ + 2πk, где  k - целое число.

Сопряженное комплексное число в тригонометрической форме отличается только знаком перед мнимой частью: r₁(cosφ₁ - i sin φ₁).

Сложение и вычитание комплексных чисел в тригонометрической форме не возможно.

Умножение комплексных чисел в тригонометрической форме происходит следующим образом:

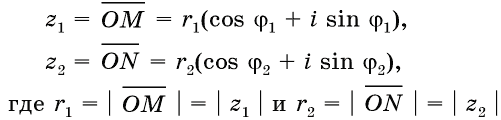
соответственно z₁ и z₂ модули этих чисел, а φ₁ и φ₂ – их аргументы. Найдем произведение этих чисел:

z₁z₂ = r₁r₂(cosφ₁ + i sin φ₁)(cos φ₂ + i sin φ₂) = r₁r₂(cos φ₁cos φ₂ – sin φ₁ sin φ₂) + i = (cos φ₁sin φ₂ + sin φ₁cos φ₂).

Воспользуемся теоремами сложения синуса и косинуса:

cos φ₁cos φ₂ – sin φ₁ sin φ₂ = cos(φ₁ + φ₂);

cos φ₁sin φ₂ + sin φ₁cos φ₂ = sin(φ₁ + φ₂).

Тогда произведение данных комплексных чисел равно комплексному числу:

z₁z₂ = r₁r₂(cos(φ₁ + φ₂) + i sin(φ₁ + φ₂)).

Последнее соотношение позволяет сформулировать правило умножения комплексных чисел: при умножении двух комплексных чисел их модули перемножаются, а их аргументы складываются.

Формула Муавра. Для любого целого числа n и любого действительного числа  имеет место следующее равенство:

.

Следствие (возведение комплексного числа в тригонометрической форме в степень). Пусть . Тогда         

.

Таким образом, при возведении в степень модуль комплексного числа возводится в степень, а аргумент умножается на степень.

Деление комплексных чисел в тригонометрической форме происходит следующим образом:

Таким образом, при делении двух комплексных чисел их модули делятся, а аргументы вычитаются.

Извлечение корней из комплексных чисел

Пример 13. Запишите комплексные числа  и  в тригонометрической форме и найдите их произведение  и частное .

Решение.

1) Комплексное число  на комплексной плоскости находится во второй четверти, поэтому

, .

2) Комплексное число  на комплексной плоскости находится во четвертой четверти, поэтому

, .

3)

.

Ответ: , .

Пример 14. Вычислить .

Решение.

Комплексное число  на комплексной плоскости находится в третьей четверти, поэтому ,

Применим формулу Муавра:

.

Пример 15. Вычислить .

Решение:

Представим число в тригонометрической форме, для чего найдём его модуль и аргумент:

- 1 = - 1 + 0 ·  i,   a = - 1, b = 0,

, k  = 0, 1, 2.

k  = 0, ;

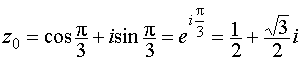k  = 1,

k  = 2, .
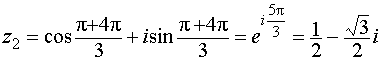