Раздел3. Основы дискретной математики, теории вероятности и математической статистики.

Тема 3.1. Основы дискретной математики.

План:

1. Множества и отношения между ними.

2. Понятие графа.

Пункт 1. Множества и отношения между ними.

1. Понятие множества.

Понятие множества принадлежит к числу фундаментальных неопределяемых понятий. Опр.3.1. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называют элементами. Элементы множества отличают друг от друга. Например, множество всех книг в библиотеке или множество вершин многоугольника.

Множества обозначаются большими буквами. Например, A, B, C, X, N и т.д. Если объект a является элементом множества A, то говорят, что a принадлежит A. Это записывается, как 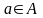. Запись будет означать, что a не является элементом A.

Множества как объекты могут быть элементами других множеств.

Опр.3.2. Множества, элементами которых являются другие множества, называются классом или семейством.

Опр.3.3. Множество, не содержащее элементов, называется пустым и обозначается .

2. Задание множеств.

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать разными способами:

• перечислением М элементов: ;

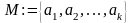• характеристическим свойством: ;

Перечисление задается в фигурных скобках, через запятую.

Здесь и далее фигурными скобками будем обозначать множество, в котором не играет роли порядок следования элементов, и круглыми скобками последовательность, в которой порядок следования элементов важен.

Пример 3.1.

.

.

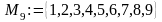3. Операции над множествами

Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Элементы множества изображаются точками внутри круга, если они принадлежат множеству (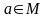 на рис 3.1 а), и точками вне круга, если они множеству не принадлежат ( ).

а)

б)

Рис. 3.1. Иллюстрация кругами Эйлера

Будем также использовать символы 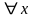вместо слов «для любых х», «каждый элемент х» и 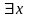вместо слов «существует х».

Сравнение множеств.

Опр.3.4. Множество A содержится во множестве B (множество B включает в себя множество A), если каждый элемент A принадлежит также и B (рис 1.1 б):

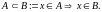
В этом случае A называется подмножеством B, а B – надмножеством A.

Опр.3.5. Если и 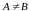, то A называется собственным подмножеством B.

Опр.3.6. Два множества равны, если они являются подмножествами друг друга, т.е. .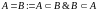

Мощность множества обозначается как |М|. Для конечных множеств мощность – это число элементов. Например, 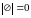, но .

Опр.3.7. Если А=В, то множества A и B называются равномощными.

Пример 3.2.

Множество решений (корней) уравнения 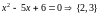, т.е. 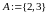. Множество простых чисел, меньших пяти . Следовательно, А=В.

Опр.3.8. Если в множестве A найдется хотя бы один элемент, не принадлежащий B, то A не является подмножеством B, т.е. .

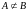Пример 3.3.

Интервал 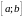не является подмножеством промежутка , так как , но .

Из определения следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение 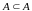. Полагают, что  является подмножеством любого множества.

Пример 3.4.

Рассмотрим множество, состоящее из трех элементов: 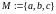. Найдем все его подмножества:

а) пустое ;

б) по одному

в) по два

г) по три .

Число всех подмножеств составляет 8=2³. Если множество состоит из n элементов, то число всех подмножеств равно 2ⁿ. Или булеан |2М|=2|М|.