
- •Раздел3. Основы дискретной математики, теории вероятности и математической статистики.
- •Тема 3.1. Основы дискретной математики.
- •Множества и отношения между ними.
- •Понятие графа.
- •Понятие множества.
- •Задание множеств.
- •Операции над множествами
- •Сравнение множеств.
- •Пересечение множеств.
- •Объединение множеств.
- •Разность множеств.
- •Симметричная разность
- •2.1. Понятие графа.
- •2.2. Виды графов.
- •2.3. Связность графов.
- •2.4. Примеры приложений теории графов.
Пересечение множеств.
Опр.3.9.
Множество, состоящее из всех элементов,
принадлежащих и множеству A, и множеству
B, называется пересечением
и обозначается
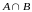 .
.
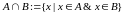 .
.
Пример 3.5.
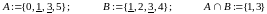 .
.
Если
же множества A и B не имеют общих элементов,
то их пересечением является пустое
множество, то есть
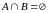 .
Например, пересечение множества четных
чисел с множеством нечетных.
.
Например, пересечение множества четных
чисел с множеством нечетных.
Пересечение
пустого множества с любым множеством
– пустое множество:
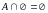 .
.
Свойства пересечения
1.
Коммутативность (переместительное
свойство).
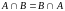 .
.
2.
Ассоциативность.
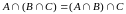 .
.
3.
Свойство нуля.
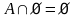 .
.
4.
Идемпотентность
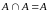 .
.
5. Дистрибутивность.
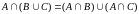 ;
;
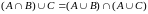
6.
Свойство единицы. Если задан универсум
U и любые
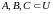 ,
то можно записать:
,
то можно записать:
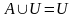 (рис. 3.2 а);
(рис. 3.2 а);
 (рис. 3.2 б).
(рис. 3.2 б).

Объединение множеств.
Опр.3.10.
Множество, состоящее из всех элементов,
принадлежащих или множеству A, или
множеству B, называется объединением
множеств. Обозначается так:
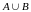 .
.
Пример 3.6.
Даны
множества
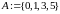 и
и
 .
Их объединением будет
.
Их объединением будет
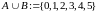 .
.
Пример 3.7.
Даны
числовые промежутки (рис. 3.3). Их
объединением будет
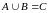 .
.

Рис. 3.3. Множества точек отрезков
Объединение и пересечение множеств хорошо иллюстрируются на плоскости (рис. 3.4). При этом множества изображаются кругами или прямоугольниками.
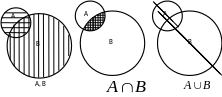
Рис. 3.4. Операции над множествами
Свойства объединения
1. Коммутативность
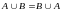 .
.
2.
Ассоциативность.
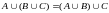 .
.
3.
Свойство нуля.
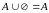 .
.
4.
Идемпотентность
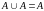 .
.
5.
Дистрибутивность.
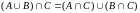 .
.
Разность множеств.
Записывается
так:
 .
.
Геометрическое представление разности множеств на рис. 3.5.
Симметричная разность
Геометрическая интерпретация симметрической разности множеств представлена на рис. 3.6.
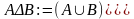 ;
;
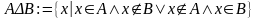 .
.


Рис. 3.5. Разность множеств Рис. 3.6. Симметричная разность
Д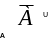 ополнение
множеств
ополнение
множеств
Геометрическое представление
дополнения множеств представлена на рис.рис. 3.7.
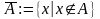 ;
;
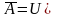 .
Рис. 3.7. Дополнение множеств
.
Рис. 3.7. Дополнение множеств
Свойства дополнения
 :
:
1)
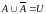 ; 3)
; 3)
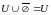 ; 5)
; 5)
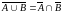 ;
;
2)
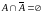 ; 4)
; 4)
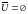 ;
6)
;
6)
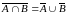 .
.
Пример 3.8.
Рассмотрим
операцию дополнения множества, являющегося
пересечением множеств A и B. Её результат
совпадает с объединением дополнений
этих множеств, (свойство 6)
 ;
в этом можно убедиться с помощью диаграмм
Эйлера – Венна (рис. 3.8).
;
в этом можно убедиться с помощью диаграмм
Эйлера – Венна (рис. 3.8).
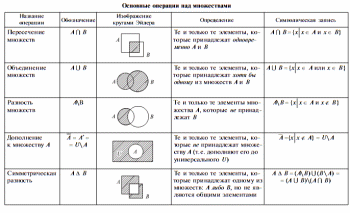

Рис. 3.8. Геометрическая иллюстрация свойства 6
Все основные операции над множествами можно записать в одну таблицу.
Пункт 2. Понятие графа.
2.1. Понятие графа.
Понятие графа опирается на основные понятия теории множеств, так как граф можно рассматривать как объект, состоящий из двух множеств - множества точек (вершин) X и множества линий (рёбер) U, которые соединяют некоторые вершины. При этом совершенно несущественно, соединены ли вершины графа отрезками прямых линий или криволинейными дугами, какова длина линий, как расположены вершины графа на плоскости и другие геометрические характеристики графа. Каждое ребро представляет собой неупорядоченную пару вершин из множества X.
Опр.3.11. Графом называется объект, состоящий из множества точек (вершин) X и множества линий (рёбер) U, которые соединяют некоторые вершины.
Математическая запись графа включает обозначения множеств вершин и рёбер, например, G = (X, U), где X - множество вершин; U - множество рёбер.
Пример изображения графа G, состоящего из множества вершин X = {x1, x2, x3, x4, x5} и множества рёбер U = {u12, u13, u14, u15, u24, u25, u35} представлен на рис. 3. 9.
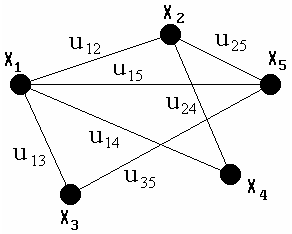 Рис.
3.9. Граф, состоящий из множества вершин
Х и множества ребер U.
Рис.
3.9. Граф, состоящий из множества вершин
Х и множества ребер U.
Элементы множеств X и U могут содержать индексы. Индексы вершин обозначают их номера. Индексы рёбер обозначают номера соединяемых ими вершин. Запись uij означает, что ребро графа образовано парой вершин xi и xj:
uij = (xi, xj), xi є X, xj є X.
