- •Гринфельд г.М. - Теория автоматического управления Оглавление
- •1. ОсновНые понятия и определения теории автоматического управления
- •1.1. Обобщенная структурная схема сау
- •1.2. Классификация сaу
- •2. Математическое описание линейных сау
- •2.1. Составление и линеаризация дифференциальных уравнений сау
- •2.2. Основные свойства преобразования Лапласа. Операторные уравнения сау. Передаточные функции линейных звеньев и систем
- •Основные свойства (теоремы) преобразования Лапласа
- •Изображения по Лапласу типовых сигналов
- •2.3. Временные и частотные характеристики звенев и систем
- •2.4. Элементарные звенья систем автоматического управления
- •Пропорциональное (усилительное, безинерционное, масштабирующее) звено
- •Интегрирующее звено
- •Идеальное дифференцирующее звено
- •Апериодическое звено первого порядка
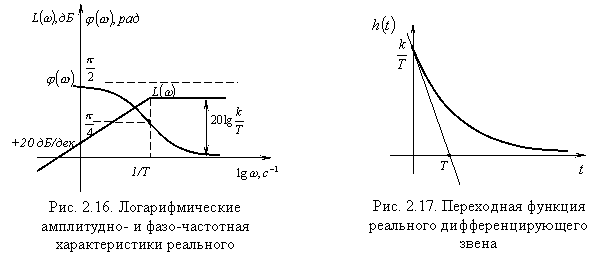
- •Реальное дифференцирующее звено
- •Инерционное звено второго порядка
- •Звено чистого запаздывания
- •Интегро-дифференцирующее звено порядка
- •Пропорционально-интегральный регулятор (пи-регулятор)
- •2.5. Неминимально-фазовые звенья
- •2.6. Эквивалентные преобразования структурных схем линейных сау
- •2.7. Передаточные функции многоконтурных систем
- •Вопросы для самопроверки
- •3. Анализ устойчивости линейных сау
- •3.1. Понятие устойчивости линейных систем
- •3.2. Алгебраический критерий устойчивости Гурвица
- •3.3. Частотные критерии устойчивости Михайлова и Найквиста
- •3.4. Запасы устойчивости
- •3.5. Оценка устойчивости по логарифмическим амлитудно- и фазо-частотным характеристикам
- •3.6. Устойчивость систем с запаздыванием
- •Вопросы для самопроверки
- •4. Качество динамических характеристик сау
- •4.1. Показатели качества процесса регулирования
- •4.2. Частотные критерии качества
- •4.3. Корневые критерии качества
- •4.4. Интегральные критерии качества
- •Вопросы для самопроверки
- •5. Оценка точности сАу
- •5.1. Стационарные режимы сау. Передаточные функции статических и астатических систем
- •5.3. Системы комбинированного управления
- •Вопросы для самопроверки
- •6. Анализ сау в пространстве состояния
- •6.1. Основные положения метода переменных состояния
- •6.2. Способы построения схем переменных состояния
- •Метод прямого программирования
- •Метод параллельного программирования
- •Метод последовательного программирования
- •6.3. Решение уравнений состояния линейных стационарных сау. Вычисление фундаментальной матрицы
- •Вопросы для самопроверки
- •7. Коррекция линейных сАу
- •7.1. Цели и виды коррекции
- •Последовательные корректирующие звенья
- •Параллельные корректирующие звенья
- •7.2. Частотный метод синтеза корректирующих устройств
- •Построение лах в низкочастотном диапазоне
- •Построение лах в среднечастотном диапазоне
- •Зависимость колебательности от значений hи h1
- •Построение лах в высокочастотном диапазоне
- •7.3. Последовательные корректирующие устройства
- •7.4. Параллельные корректирующие устройства
- •7.5. Техническая реализация корректирующих звеньев
- •Пассивные четырехполюсники постоянного тока
- •Пассивные корректирующие четырехполюсники
- •Активные корректирующие звенья
- •Активные четырехполюсники постоянного тока
- •Вопросы для самопроверки
- •8. Нелинейные системы автоматического управления
- •8.1. Особенности нелинейных систем и методы их анализа
- •8.2. Исследование нелинейных систем на фазовой плоскости
- •8.3. Метод гармонической линеаризации нелинейных звеньев
- •Коэффициенты гармонической линеаризации типовых нелинейностей
- •Вопросы для самопроверки
- •Курсовая работа
- •Задание для расчета линейной caу
- •Варианты задания для расчета линейной сау
- •Варианты передаточных функций линейной сау
- •Задание для расчета нелинейной сау
- •Варианты задания для расчета нелинейной сау
- •Варианты структурных схем нелинейных систем
- •Варианты статических характеристик нелинейного элемента
- •Экзаменационные вопросы
- •Литература
Инерционное звено второго порядка
Инерционное звено второго порядка – это звено, зависимость между выходным и входным сигналами которого описывается следующим дифференциальным уравнением:
![]()
 гдеk, T– соответственно
коэффициент усиления и постоянная
времени звена;
гдеk, T– соответственно
коэффициент усиления и постоянная
времени звена;
![]() -
коэффициент демпфирования.
-
коэффициент демпфирования.
Операторное уравнение звена:
![]()
Передаточная функция звена:
![]() .
(2.51)
.
(2.51)
Примерами реализации инерционного звена второго порядка являются RLC-контур, состоящий из катушки индуктивности, резистора и конденсатора, или физический маятник.
Амплитудно- и фазо-частотная характеристики:
A(ω)![]() ;
;
![]() .
(2.52)
.
(2.52)
В зависимости от значения коэффициента
демпфирования
![]() свойства
инерционного звена второго порядка
изменяются настолько существенно, что
при различных значениях
свойства
инерционного звена второго порядка
изменяются настолько существенно, что
при различных значениях
![]() это
звено имеет различные названия:консервативное, колебательноеилиапериодическое звено второго
порядка.
это
звено имеет различные названия:консервативное, колебательноеилиапериодическое звено второго
порядка.
1)
Консервативное звено:![]() ,
передаточная функция (2.51) принимает
вид:
,
передаточная функция (2.51) принимает
вид:
![]() .
(2.53)
.
(2.53)
При этом ее полюса чисто мнимые:
![]() .
.
В соответствии с (2.15) и (2.23) выражения переходной функции и функции веса консервативного звена:
![]()
![]() ;
;
![]() =
=![]() .
.
1)
Колебательное звено:
![]() ,
полюса передаточной функции (2.51) –
комплексно-сопряженные числа. С учетом
(2.52) логарифмическая амплитудно-частотная
характеристика звена примет вид:
,
полюса передаточной функции (2.51) –
комплексно-сопряженные числа. С учетом
(2.52) логарифмическая амплитудно-частотная
характеристика звена примет вид:
![]() .
.
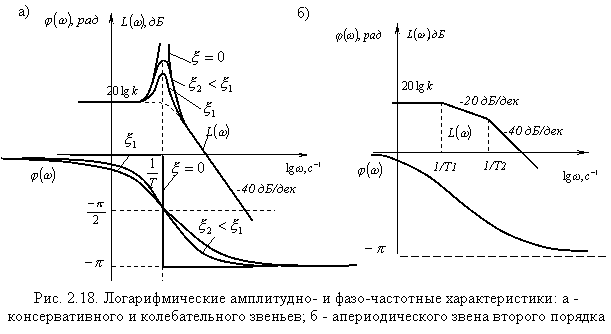
Кусочно-асимптотическая ЛАЧХ звена
состоит из двух участков. На низкочастотном
участке до частоты сопряжения
![]() уравнение
горизонтальной асимптоты:
уравнение
горизонтальной асимптоты:
![]() ,
,
а в диапазоне частот много больше частоты сопряжения уравнение высокочастотной асимптоты:
![]()
Последнее уравнение – это уравнение прямой с наклоном -40 дБ/дек.
В окрестности частоты сопряжения график
ЛАЧХ колебательного звена при
![]() имеет
амплитудный всплеск («горб»), величина
которого тем больше, чем меньше коэффициент
демпфирования
имеет
амплитудный всплеск («горб»), величина
которого тем больше, чем меньше коэффициент
демпфирования
![]() .
У консервативного звена при
.
У консервативного звена при
![]() амплитудный
всплеск вырождается в разрыв непрерывности.
амплитудный
всплеск вырождается в разрыв непрерывности.
Выражения переходной функции и функции веса колебательного звена:
![]()
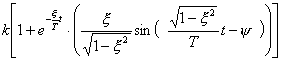 ;
;
![]() =
=
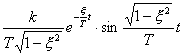 ;
;
где
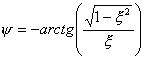 .
.
2)
Апериодическое звено второго
порядка:
![]() ,
полюса передаточной функции (2.51) –
действительные числа, поэтому передаточную
функцию звена можно представить в
следующем виде:
,
полюса передаточной функции (2.51) –
действительные числа, поэтому передаточную
функцию звена можно представить в
следующем виде:
![]() .
(2.54)
.
(2.54)
Очевидно, что между коэффициентами передаточных функций (2.51) и (2.54) существуют следующие зависимости:
|
|
|
![]() и
и
![]()
![]() .
.
Уравнения логарифмических амплитудно- и фазо-частотной характеристик:
![]()
![]() ;
;
![]()
![]() .
.
 Выражения
для временных характеристик апериодического
звена второго порядка:
Выражения
для временных характеристик апериодического
звена второго порядка:
![]()
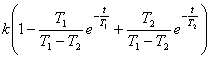 ;
;
![]() =
=
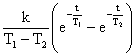 .
.
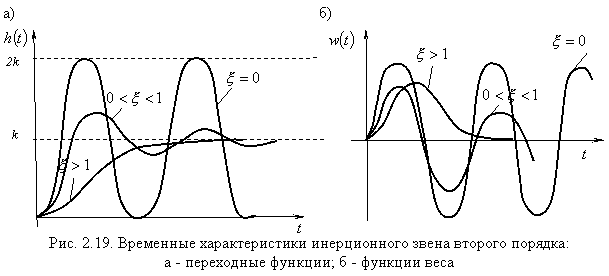
Графики логарифмических амплитудно- и фазочастотной характеристик инерционного звена второго порядка для различных значений коэффициента демпфирования приведены на рис. 2.18; графики временных характеристик – на рис. 2.19.
Звено чистого запаздывания
Звено чистого запаздывания – это
звено, выходной сигнал которого полностью
совпадает по форме с входным сигналом,
но отстает от него на время
![]() ,
т.е.
,
т.е.
![]() .
.
На основании теоремы запаздывания
(2.11):
![]()
![]() .
Следовательно, передаточная функция
звена имеет вид:
.
Следовательно, передаточная функция
звена имеет вид:
![]() ,
,
где
![]() –
время запаздывания.
–
время запаздывания.
Частотные характеристики для звена чистого запаздывания:
![]() cos(ω)
– j sin
(ω);
cos(ω)
– j sin
(ω);
т.е. P(ω) = cos(ω) и Q(ω)= – sin (ω);
A(ω)= 1,
![]() ω
ω![]() ,
, ![]() .
.
На рис.2.20 приведен график переходной функции звена, на рис.2.21 – годограф АФХ, а на рис. 2.22 – логарифмические амплитудно- и фазо-частотные характеристики.