Исследование элементарных звеньев в Матлабе

Цель работы: изучение временных и частотных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК – MATLAB.

Исходные данные: даны динамические звенья с параметрами: усилительное звено(к=2) ; апериодическое звено(к=4,Т=0.4);колебательное звено (к=1,Т1=0.6,Т2=2.4); интегрирующее звено(к=8,Т=0.5); дифференцирующее звено(к=6,Т=0.2).

1. Апериодическое звено.

-переходная ф-ция

-передаточная ф-ция

-АФХ

-АЧХ

-ФЧХ

Структурная схема звена:

Переходная ф-ция.

Импульсная ф-ция.

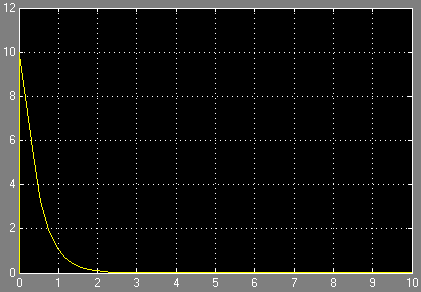
АФХ

1) k=4;T=0.4;w=0:0.01:50;W=k./(T.*j.*w+1);

2) Title('W=k./(T.*j.*w+1)');

3) xlabel('Real');ylabel('Imag');

4) plot(real(W),imag(W),'B');

АЧХ

1) k=4; T=0.4; w=0:0.01:25; A=k./sqrt((T.*w).^2 +1);

2) plot(w , A, 'B');

3) grid on;

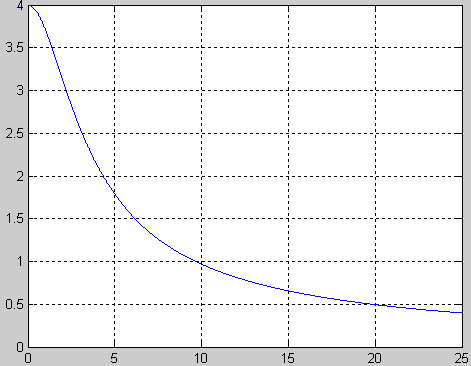
ФЧХ

1) T=0.4;

2) w=0:0.01:25;

3) F=-atan(w.*T);

4) plot(w,F,'B');

5) grid on;

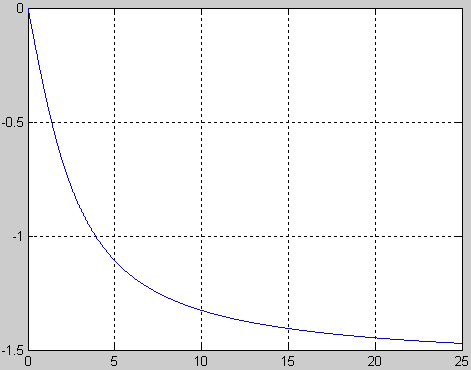
Вывод: апериодическое звено характеризуется двумя параметрами: Т- постоянная времени(время переходного процесса) , к- коэффициент усиления (характеризует увеличение амплитуды выходного сигнала по сравнению с входным). При подачи на вход передаточной ф-ции единичного ступенчатого сигнала(переходная ф-ция ) величина выходного сигнала плавно увеличивается от 0 до постоянного значения равного к. При подачи на вход передаточной ф-ции единичного импульса (импульсная ф-ция ) величина выходного сигнала плавно уменьшается от к/Т до постоянного значения равного 0.АФХ звена представляет собой полуокружность с радиусом равным к/2. ФЧХ звена плавно уменьшается от 0 до –π/2. АЧХ звена плавно уменьшается от к до 0.

2. Колебательное звено.

-передаточная ф-ция

-АФХ

-АЧХ

-ФЧХ

Структурная схема звена:

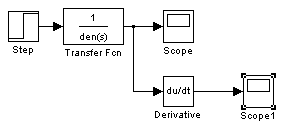
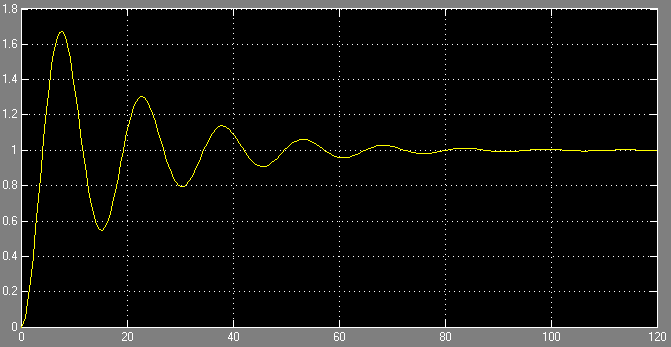
Переходная ф-ция.

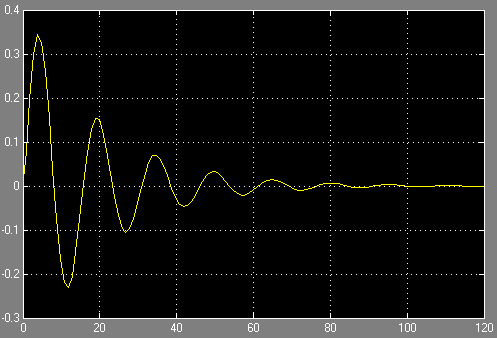
Импульсная ф-ция.

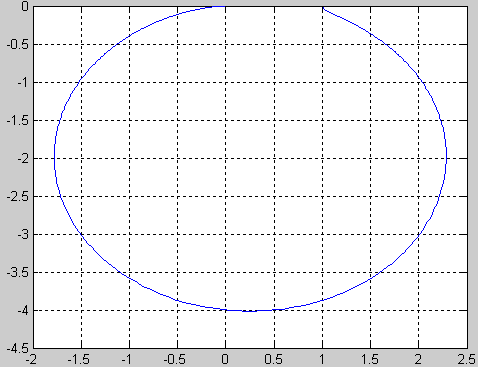
АФХ

1) k=1;

2) T1=0.6;T2=2.4;

3) w=0:0.001:100;

4) W=k./(-(T2.*w).^2+T1.*j.*w+1);

5) plot(real(W),imag(W));grid on;

АЧХ

1) k=1;

2) T1=0.6;T2=2.4;

3) w=0:0.01:3;

4) A=k./sqrt((1-(w.*T2).^2).^2+(w.*T1).^2);

5) plot(w,A);grid on;

ФЧХ

1) T1=0.6;

2) T2=2.4;

3) w=0:0.001:1.5;

4) F=-atan(w.*T1./(1-(w.*T2).^2));

5) plot(w,F);grid on;

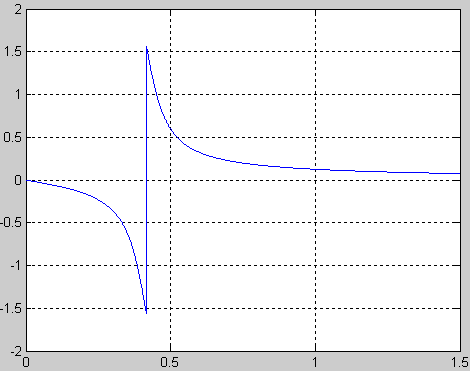
Вывод: колебательное звено характеризуется тремя параметрами: Т1 и Т2- постоянные времени, к- коэффициент усиления (характеризует увеличение амплитуды выходного сигнала по сравнению с входным). При подачи на вход передаточной ф-ции единичного ступенчатого сигнала(переходная ф-ция ) величина выходного сигнала представляет собой затухающие колебания, которые уменьшаются до постоянного значения равного к . При подачи на вход передаточной ф-ции единичного импульса (импульсная ф-ция ) величина выходного сигнала представляет собой затухающие колебания, которые уменьшаются до постоянного значения равного 0. АФХ звена при ω=0 имеет значение к , а при ω→ ∞ АФХ стремится к 0. АЧХ и ФЧХ при некотором значении ω (в данном случае ω ‹ 0.5 ) имеют скачок.

3. Усилительное(пропорциональное)звено.

- Передаточная ф-ция

-АФХ

-АЧХ

-ФЧХ

Структурная схема звена:

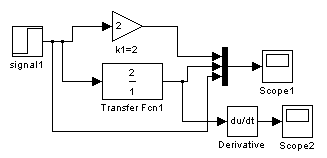
Переходная ф-ция.

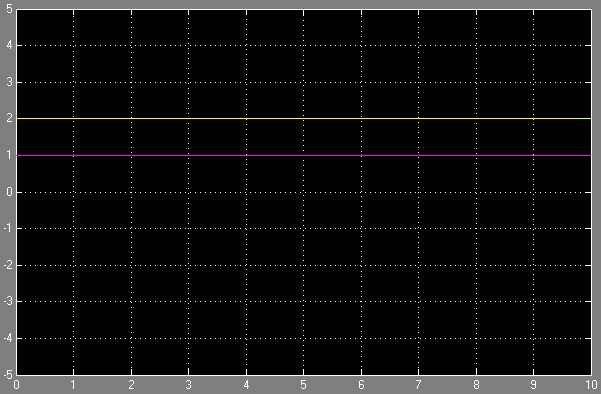
Импульсная ф-ция.

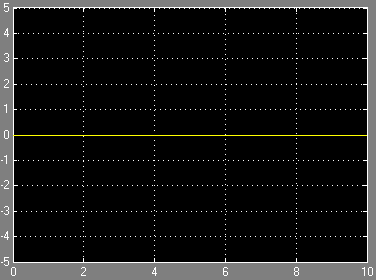
АФХ

1) k=2;

2) w=0:0.01:10;

3) W=k;

4) plot(w,W,'-R');

5) grid on;

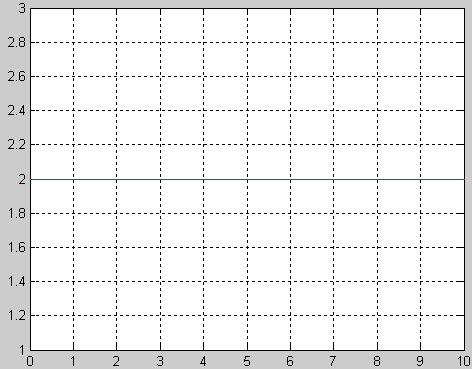
АЧХ

1) k=2;

2) w=0:0.01:10;

3) W=k;

4) plot(w,А,'-R');

5) grid on;

ФЧХ

1) k=2;

2) w=0:0.01:5;

3) F=0;

4) plot(w,F,'-R');

5) grid on;

Вывод: усилительное звено характеризуется одним параметром: к- коэффициент усиления (характеризует увеличение амплитуды выходного сигнала по сравнению с входным). При подачи на вход передаточной ф-ции единичного ступенчатого сигнала(переходная ф-ция ) выходной сигнал повторяет входной, но с амплитудой большей амплитуды входного сигнала в к раз. При подачи на вход передаточной ф-ции единичного импульса (импульсная ф-ция ) выходной сигнал полностью повторяет входной, т.е. 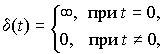. АФХ звена имеет постоянное значение равное к при любом значении ω. АЧХ совпадает с АФХ звена. ФЧХ звена имеет постоянное значение равное 0 при любом значении ω.

4. Интегрирующее звено.

-Передаточная ф-ция

-АФХ

-АЧХ

-ФЧХ

Структурная схема звена:

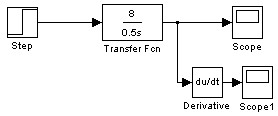
Переходная ф-ция.

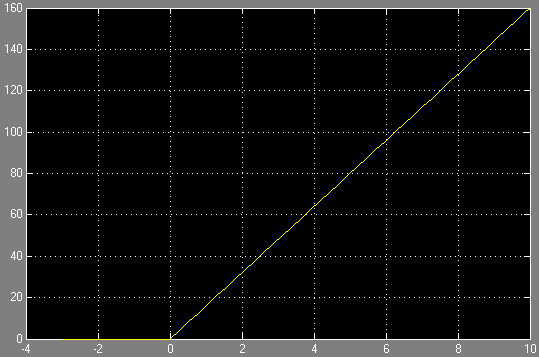
Импульсная ф-ция.

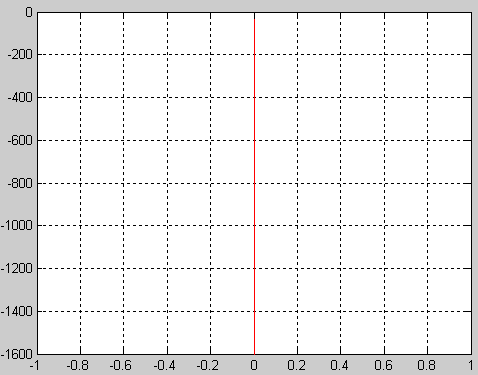
АФХ

1) k=8;

2) T=0.5;

3) w=0:0.01:1;

4) W=-j.*k./(T.*w);

5) plot(real(W),imag(W),'R');grid on;

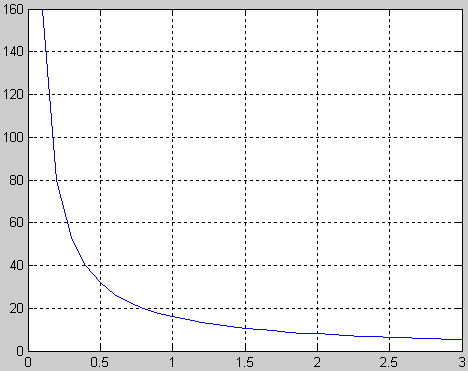
АЧХ

1) k=8; T=0.5;w=0:0.1:3;

2) A=k./(T.*w);

3) plot(w,A); grid on;

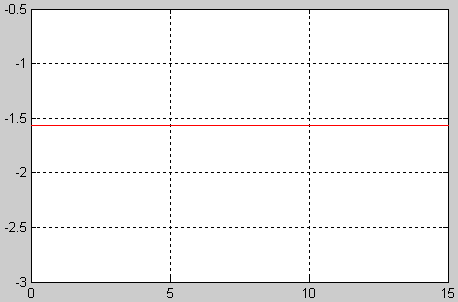
ФЧХ

1) w=0:0.001:15;

2) F=-pi/2;

3) plot(w, F,'R');grid on;

Вывод: интегрирующее звено характеризуется двумя параметрами: Т- постоянная времени , к- коэффициент передачи звена по скорости(численно равный скорости изменения выходной величины при единичном значении входной величины). При подачи на вход передаточной

ф-ции единичного ступенчатого сигнала(переходная ф-ция ) величина выходного сигнала постоянно растёт ,при этом чем больше значение к ,тем круче хар-ка (т.е. больше угол между осью абсцисс и переходной ф-цией). При подачи на вход передаточной ф-ции единичного импульса (импульсная ф-ция ) величина выходного сигнала принимает значение равное к/Т и остаётся постоянной . АФХ звена представляет собой прямую уходящую в бесконечность под углом –π/2 к оси абсцисс. ФЧХ звена постоянная и имеет значение –π/2. АЧХ имеет вид кривой асимптотически приближающейся к осям ОХ и ОУ при изменении ω от 0 до ∞.Для интегрирующего звена характерно то, что при отсутствии входного сигнала выходной сигнал является постоянным , если на входе есть сигнал , то выходной сигнал растёт.

5. Дифференцирующее звено.

-Передаточная ф-ция или

-АФХ

-АЧХ

-ФЧХ

Структурная схема звена:

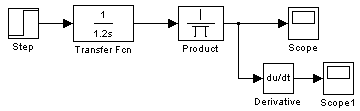
Переходная ф-ция.

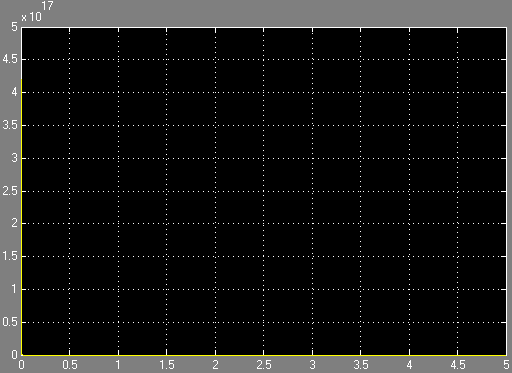
Импульсная ф-ция.

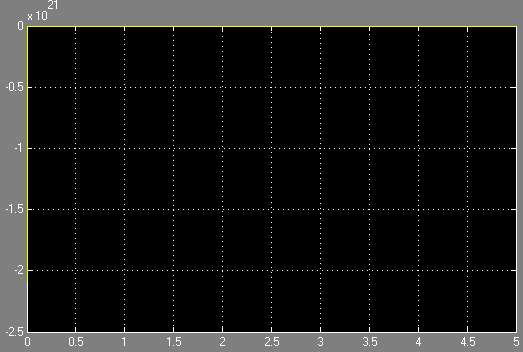
АФХ

1) k=6;

2) T=0.2;

3) w=0:0.01:50;

4)W=k.*T.*j.*w;

5) plot(real(W),imag(W),'R'); grid on;

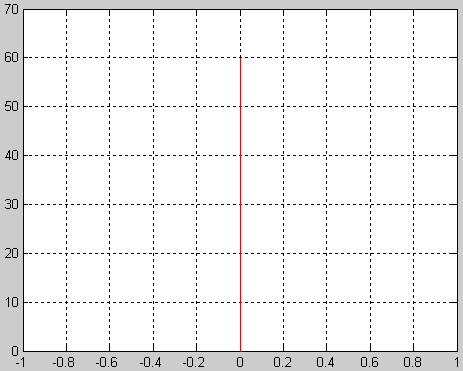
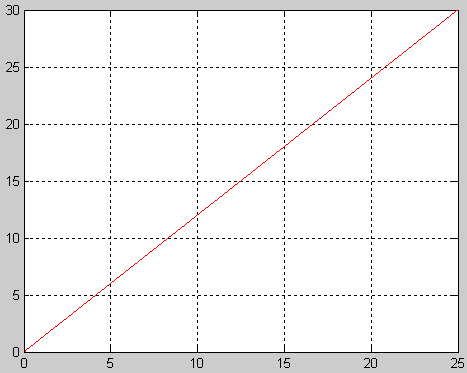
АЧХ

1) k=6;

2) T=0.2;

3) w=0:0.01:25;

4) A=k.*w.*T;

5) plot(w,A,'R');grid on;

ФЧХ

1) w=0:0.01:5;

2) F=pi/2;

3) plot(w, F, 'R');grid on;

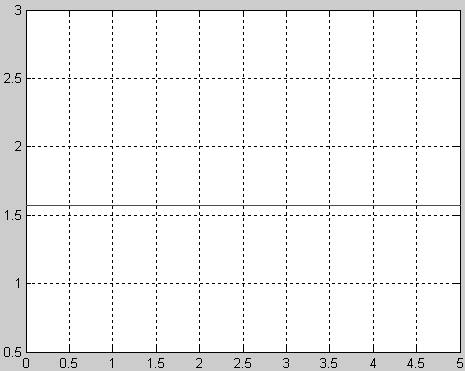
Вывод: апериодическое звено характеризуется двумя параметрами: Т- постоянная времени, к- коэффициент усиления .АФХ звена представляет собой прямую уходящую в бесконечность под углом π/2 к оси абсцисс . АЧХ растёт пропорционально росту ω. ФЧХ звена постоянная и имеет значение π/2. Выходная величина пропорциональна скорости изменения входной величины. Передаточная функция, частотные характеристики дифференцирующего звена обратны передаточной функции и соответствующим характеристикам интегрирующего звена.