Зависимость колебательности от значений hи h1

М	h	h1
		ЛАХ типа А	ЛАХ типа B	ЛАХ типа C	ЛАХ типа D
1,1	21,00	5,5	2,05	5,5	1,9
1,3	7,70	8,9	3,85	8,9	2,8
1,5	7,00	12,75	4,8	12,5	3,6
2,0	3,00	28,0	10,0	26,6	6,1
2,.5	2,33	42,0	14,1	40,0	7,2

 

Построение лах в высокочастотном диапазоне

Вид желаемой ЛАХ в высокочастотном диапазоне определяет, например, такой показатель, как помехоустойчивость системы, но на качество регулирования поведение  в этой частотной области вид ЛАХ влияет в незначительной степени. Поэтому на участке высоких частот с целью упрощения корректирующего звена допустимо совпадение наклонов асимптот желаемой ЛАХ и ЛАХ исходной нескорректированной системы.

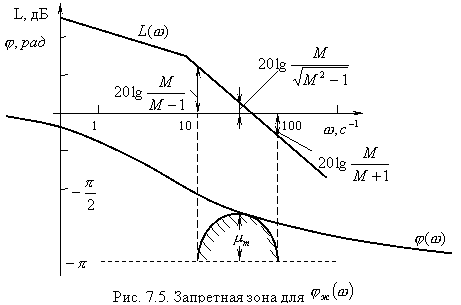
Завершив построение желаемой ЛАХ разомкнутой системы, необходимо определить соответствующую ей фазо-частотную характеристику , и проверить наличие необходимого запаса устойчивости системы по амплитуде  и по фазе .  В случае, когда при коррекции системы указано требуемое значение показателя колебательности , необходимо построить запретную зону для   (рис. 7.5).

Границы запретной зоны, называемые  -кривыми, для различных значений приведены на рис. 7.6 . Запретная зона строится в частотном диапазоне, в котором

 <  < .

Максимальное значение запаса по фазе  соответствует частоте, при которой = . Величина запретной зоны возрастает при уменьшении . Если фазо-частотная характеристика  заходит в запретную зону, то фактическая величина  показателя колебательности превышает максимально допустимое значение.

7.3. Последовательные корректирующие устройства

В соответствии с выражением (7.1) АФХ разомкнутой скорректированной системы равна:

,                                            (7.5)

а логарифмические амплитудно- и фазо-частотные характеристики соответственно:

;                                               (7.6)

.                                              (7.7)

Из выражений (7.6) и (7.7) следует, что амплитудно- и фазо-частотные характеристикипоследовательно корректирующего звена равны:

;                                               (7.8)

.                                              (7.9)

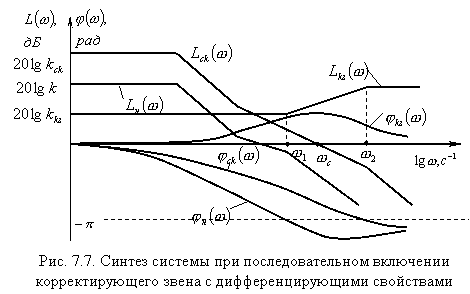
В качестве примера на рис.7.7 приведены логарифмические частотные характеристики разомк­нутой нескорректированной системы ( и ). На этом же рисунке представлена желаемая ЛАХ скорректиро­ванной системы и соответствующая ей фазо-частотная характеристика . В соответствии с выражением (7.8), вычитая из же­лаемой ЛАХ характеристику исходной системы , получаем ЛАХ корректирующего звена . Приведенная на рис.7.7 соответствует интегро-дифференцирующему звену:

с дифференцирующими свойствами в среднечастотном диапазоне ( > ). Параметры корректирующего звена опре­деляются следующим образом:

;                                        .

Значения сопрягающих частот  и , а также ве­личина  берутся из рис. 7.7.

Для уточнения действительного запаса устойчивости по модулю и фазе синтезированной системы на рис.7.7 построена логарифмическая фазо-частотная характеристика . Как видно из рис. 7.7, запасы устойчивости по фазе и по модулю скорректи­рованной системы больше соответствующих запасов устойчивости  исходной системы.

Из рассмотренного примера следует, что достоинство коррекции с помощью последовательных дифференцирующих устройств заключается в том, что при обеспечении требуемого запаса устойчивости одновременно увеличивается частота среза и возмож­но увеличение коэффициента усиления системы, в ре­зультате чего умень­шаются время регулирования и установившаяся ошибка.

Однако после­довательная коррекция с помощью дифференцирующих устройств имеет и не­достатки, заключающиеся в значительном увеличении усиления в области высоких  частот. Если при этом на полезный входной сигнал системы накладываются высокочастотные помехи, степень их подавления в скорректированной системе будет ниже, чем в нескорректированной. Помехоустойчивость системы может быть повышена путем снижения коэффициента усиления системы, но это приведет к снижению точности регулирования.

Для исключения существенного ослабления коэффициента усиления системы на низких частотах в качестве последовательного корректирующего звена можно использовать интегро-дифференцирующее зве­на с преобладающими интегрирующими свойствами, т.е. при  <  (рис. 7.8).

Как вид­но из рис. 7.8, исходная нескорректированная система не только не обеспечи­вает требуемого качества регулирования, но даже яв­ляется неустойчивой. Без корректирующего устройства требуемый запас устойчивости в системе можно обеспечить только за счет большого снижения коэффициента усиления системы, что яв­ляется нежелательным.

Желаемую ЛАХ скорректированной системы можно получить при последовательном включении корректирую­щего устройства с интегрирующими свойствами. Из рис. 7.8 следует, что наряду с относительным уве­личением коэффициента усиления системы на низких ча­стотах существенно умень­шено усиление на высоких частотах и тем самым ослаблено влияние высокочастотных помех.

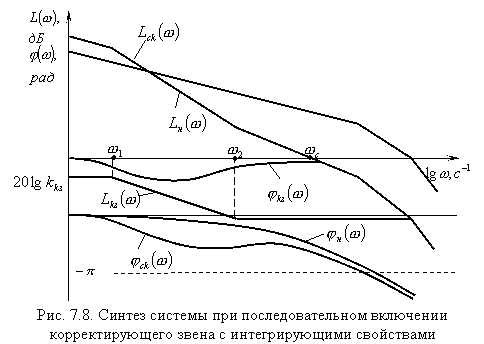
Недостатком таких корректирующих устройств является то, что при их использовании уменьшается частота среза и, следователь­но, длительность переходных процессов в системе уве­личивается.

При решении практических инженерных задач по син­тезу структуры САУ широкое применение находят по­следовательные корректирующие устройства в виде ком­бинированных интегро-дифференцирующих звеньев.

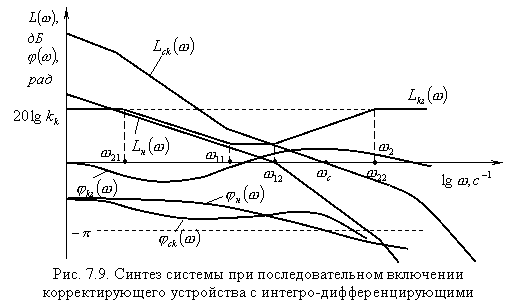
Пример синтеза желаемых логарифмических частот­ных характеристик системы с помощью последовательного комбинированного интегро-дифференцирующего звена представлен на рис.7.9.

Из рис.7.9 следует, что при правильно выбранных параметрах корректирую­щего устройства можно обеспечить требуемую точность регулирования в установившихся режимах и одновременно повысить качество переходного процесса, по сравнению с исходной системой. Передаточная функция корректирующего звена с ЛАХ , приведенной на рис. 7.9, равна:

.

При выборе коэффициента усиления корректирующе­го устройства следует исходить из условия обеспечения требуемой точности в установившихся режимах скоррек­тированной системы. Так, если коэффициент передачи ис­ходной нескорректированной разомкнутой системы равен , а требуемый ко­эффициент передачи скорректированной системы равен , то коэффициент передачи корректирующего устрой­ства должен быть равен:

.

Постоянные времени корректирующего устройства  и   необходимо выбирать так, что­бы частоты сопряжения и  были бы значительно меньше частоты среза  скорректирован­ной системы. Этим обеспечивается сдвиг интервала частот, в кото­ром корректирующее устройство создает отставание по фазе в безопасную зону слева от частоты среза.

Частоты сопряжения  и  должны быть такими, чтобы частота среза  рас­полагалась бы примерно в середине интервала частот <<. В этом случае максимальное опереже­ние, создаваемое корректирующим устройством, будет в области частоты среза, что обеспечивает в скорректированной системе наибольший запас устойчивости по фа­зе.

Зачастую не все из перечисленных рекомендаций по выбору параметров  корректирующего устройства удается удовлетворить в полной мере.  Поэтому необходимо построить ЛАХ скор­ректированной системы с учетом фактических логариф­мических частотных характеристик корректирующего устройства и проверить, например, путем моделирования системы на ЭВМ, удовлетворяет ли САУ  предъявляемым требованиям к качеству регулирования.