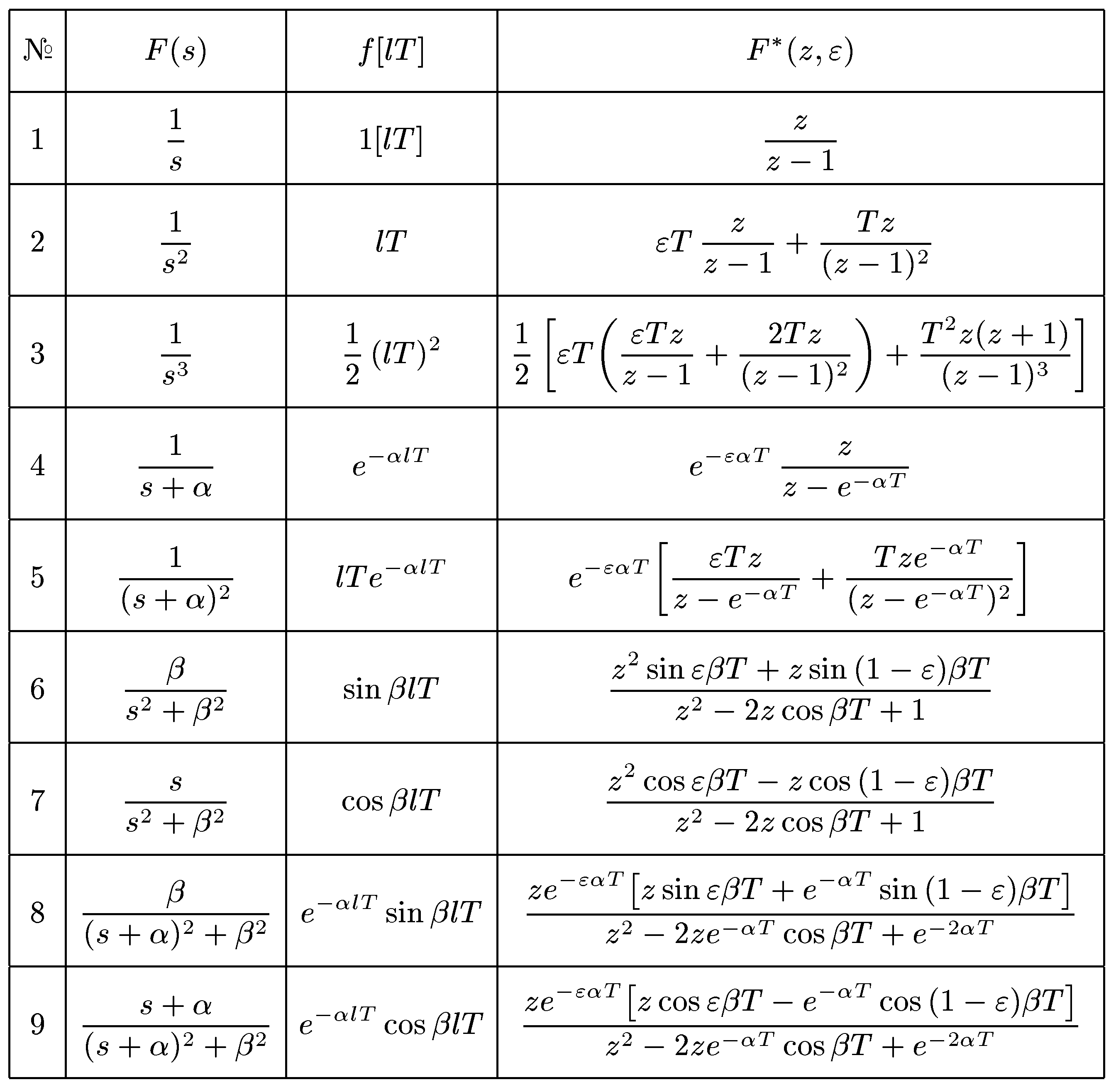- •Раздел 1. Основные понятия и определения та у 7
- •Раздел 2. Получение информации для анализа и синтеза аср. Принципы построения математических моделей элементов аср 29
- •Раздел 3. Динамические характеристики линейных систем 50
- •Раздел 4. Типовые динамические звенья. Переходные и частотные характеристики типовых звеньев 69
- •Раздел 5. Характеристики замкнутых аср 88
- •Раздел 6. Анализ устойчивости линейных систем 106
- •Раздел 7. Качество процессов управления 140
- •Раздел 8. Косвенные критерии качества 154
- •Раздел 9. Параметрический синтез типовых регуляторов 169
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср 173
- •Раздел 11. Системы регулирования при случайных воздействиях 214
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср) 245
- •Раздел 13. Анализ устойчивости дискретных систем 274
- •Раздел 14. Адаптивные системы 293
- •Раздел 1. Основные понятия и определения та у
- •1.1 Цель и задачи дисциплины. Кибернетика. Основные понятия тау. Принципы автоматического регулирования Цель и задачи дисциплины
- •Кибернетика
- •Основные понятия тау
- •Объект автоматического управления
- •Примеры объектов и систем управления
- •Примеры систем управления
- •Функциональные и структурные формы объектов
- •Принципы автоматического регулирования (управления)
- •Пример простейшей непрерывной замкнутой системы регулирования и ее функциональная схема
- •1.2 Классификация аср. Задачи курса тау Классификация аср
- •Задачи курса тау
- •Раздел 2. Получение информации для анализа и синтеза аср. Принципы построения математических моделей элементов аср
- •2.1 Принципы построения математических моделей элементов аср. Линеаризация. Примеры моделей звеньев Принципы построения математических моделей элементов аср
- •Дифференциальные уравнения
- •Составление математической модели
- •Линеаризация
- •Передаточные функции сау. Преобразования Лапласа
- •Примеры моделей звеньев
- •Раздел 3. Динамические характеристики линейных систем
- •3.1 Динамические характеристики линейных систем. Типовые входные воздействия, их спектры и изображения. Временные характеристики - импульсная (весовая) и переходная. Свойства. Уравнения свертки
- •3.2 Частотные характеристики, логарифимические частотные характеристики. Связь с передаточной функцией. Свойства и расчет частотных характеристик по передаточной функции
- •Ориентированные графы систем автоматического управления
- •Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
- •Раздел 4. Типовые динамические звенья. Переходные и частотные характеристики типовых звеньев
- •Минимально фазовые и неминимально фазовые звенья
- •Типовые звенья. Характеристики звеньев
- •Раздел 5. Характеристики замкнутых аср
- •Замкнутые системы автоматического управления. Виды обратной связи
- •Передаточные функции в системах автоматического управления
- •Комбинированные аср
- •Каскадные аср
- •Расчёт настроек регуляторов в каскадных аср
- •Последовательность расчёта настроек регуляторов
- •Раздел 6. Анализ устойчивости линейных систем
- •6.1 Понятия о критериях устойчивости. Теоремы ляпунова об оценке устойчивости по линеаризованным моделям. Критерии устойчивости рауса и гурвица Понятия о критериях устойчивости
- •Критерии устойчивости
- •Теоремы Ляпунова об оценке устойчивости по линеаризованным моделям
- •Алгебраические критерии устойчивости
- •Критерий устойчивости Гурвица
- •Критерий устойчивости Рауса
- •6.2 Критерии михайлова и найквиста. Анализ устойчивости систем с запаздыванием. Логарифмический критерий устойчивости Частотные критерии устойчивости Принцип аргумента
- •Критерий устойчивости Михайлова
- •Критерий устойчивости Найквиста
- •Устойчивость систем с запаздыванием
- •Об исследовании точности систем с запаздыванием
- •Логарифмический критерий устойчивости
- •Логарифмическая форма критерия Найквиста
- •Структурно-неустойчивые (устойчивые) системы автоматического регулирования
- •Раздел 7. Качество процессов управления
- •Методы построения переходных процессов
- •Метод Акульшина
- •Метод трапеций Солодовникова
- •Точность в установившихся режимах
- •Введение астатизма
- •Метод коэффициентов ошибок
- •Раздел 8. Косвенные критерии качества
- •8.1 Косвенные критерии качества. Корневые критерии качества — степень устойчивости и степень колебательности
- •Степень устойчивости
- •Степень колебательности
- •Частотные критерии качества
- •Запас устойчивости
- •Оценка быстродействия сар
- •Интегральные оценки качества
- •Аналитический расчет квадратичных ит-оценок
- •Раздел 9. Параметрический синтез типовых регуляторов
- •9.1 Параметрический синтез типовых регуляторов Постановка задачи синтеза. Основные методики расчета настроек регуляторов. Условия компенсации низкочастотных возмущений
- •9.2 Расчет настроек на заданную степень колебательности, Расчет настроек на заданный показатель колебательности м и me
- •9.3 Приближенные методики расчета настроек. Расчет настроек в комбинированных и каскадных аср. Робастные методы расчета настроек
- •Формульный метод определения настроек регулятора
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср
- •10.1 Нелинейные системы. Общая характеристика нелинейных аср. Типовые нелинейные модели. Уравнения нелинейных систем
- •Характеристика нелинейных систем
- •Особенности нелинейных систем
- •Типовые нелинейные элементы системы управления
- •10.2 Анализ нелинейных систем на фазовой плоскости. Классификация особых точек. Автоколебания. Метод точечных преобразований
- •Основные понятия
- •Фазовые портреты нелинейных систем
- •Методы построения фазовых портретов
- •Интегрирование уравнений фазовых траекторий
- •Метод изоклин
- •Метод припасовывания
- •Метод сшивания
- •Понятие об автоколебаниях
- •Методы исследования автоколебаний Критерий Бендиксона
- •Метод точечного преобразования y1
- •10.3 Анализ релейных систем. Понятие устойчивости по ляпунову. Устойчивость в малом, большом и целом Устойчивость в малом, большом и целом
- •Исследование устойчивости нелинейных систем. Второй метод Ляпунова
- •10.4 Абсолютная устойчивость положения равновесия. Критерий в.М. Попова Критерий в.М. Попова
- •Процедура проверки абсолютной устойчивости
- •Метод гармонической линеаризации
- •Основное уравнение метода гармонического баланса
- •Способ Гольдфарба
- •Коррекция автоколебаний
- •Условия применимости метода гармонического баланса
- •Вибрационная линеаризация
- •Раздел 11. Системы регулирования при случайных воздействиях
- •11.1 Случайные процессы в аср. Типовые случайные сигналы и их характеристики Случайные процессы в аср
- •Характеристики случайных сигналов
- •11.2 Преобразование случайных сигналов линейным звеном. Идентификация динамических характеристик при случайных процессах Преобразование случайного сигнала линейным динамическим звеном
- •Определение оптимальной передаточной функции системы управления
- •11.3 Задачи анализа и синтеза аср при случайных воздействиях. Расчет дисперсии ошибки, параметрический синтез аср по минимуму дисперсии Задачи анализа и синтеза аср при случайных воздействиях
- •Расчет ошибок с сау при случайных воздействиях
- •Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы
- •Статистическая оптимизация систем управления
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср)
- •Импульсный элемент
- •Линейные разностные уравнения
- •Раздел 1. Основные понятия и определения та у 7
- •1.1 Цель и задачи дисциплины. Кибернетика. Основные понятия тау. Принципы автоматического регулирования 7
- •Раздел 7. Качество процессов управления 140
- •Раздел 8. Косвенные критерии качества 154
- •Раздел 9. Параметрический синтез типовых регуляторов 169
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср 173
- •Раздел 11. Системы регулирования при случайных воздействиях 214
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср) 245
- •Раздел 13. Анализ устойчивости дискретных систем 274
- •Раздел 14. Адаптивные системы 293
- •Решетчатые функции и z-преобразование
- •Определение z-преобразования
- •Основные свойства z-преобразования
- •Цифровые системы управления
- •Дискретное преобразование Лапласа и частотные характеристики
- •Связь между дискретным и непрерывным преобразованиями Лапласа и непрерывная модель дискретной системы
- •12.2 Уравнения элементов цифровой аср. Цифровой регулятор, идеальный импульсный элемент, формирующий фильтр, приведенная непрерывная часть Непрерывная модель дискретной системы
- •12.3 Преобразование сигналов идеальным импульсным элементом. Теорема Котельникова. Характеристики разомкнутых цаср
- •12.4 Частотные характеристики. Характеристики замкнутых систем Динамические характеристики
- •Раздел 13. Анализ устойчивости дискретных систем
- •13.1 Анализ устойчивости дискретных систем. Необходимые и достаточные условия устойчивости. Аналог критерия гурвица Характеристическое уравнение и основное условие устойчивости
- •Алгебраические критерии устойчивости
- •Исследование устойчивости, основанное на преобразовании единичного круга в левую полуплоскость
- •Критерий устойчивости Джури
- •13.2 Аналоги критериев михайлова, найквиста Частотный критерий устойчивости
- •Критерий Найквиста
- •13.3 Методы построения переходных процессов. Косвенные критерии качества
- •Показатели качества в переходном режиме
- •Прямые показатели качества
- •Косвенные показатели качества
- •Особенности переходного процесса дискретных систем
- •Раздел 1. Основные понятия и определения та у 7
- •1.1 Цель и задачи дисциплины. Кибернетика. Основные понятия тау. Принципы автоматического регулирования 7
- •Раздел 7. Качество процессов управления 140
- •Раздел 8. Косвенные критерии качества 154
- •Раздел 9. Параметрический синтез типовых регуляторов 169
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср 173
- •Раздел 11. Системы регулирования при случайных воздействиях 214
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср) 245
- •Раздел 13. Анализ устойчивости дискретных систем 274
- •Раздел 14. Адаптивные системы 293
- •13.4 Бесконечная степень устойчивости. Регуляторы Резвика, Смита Раздел 14. Адаптивные системы
- •14.1 Классификация адаптивных систем. Системы экспериментального регулирования (сэр). Сэр с запоминанием экстремума, градиентные сэр
- •Системы экстремального регулирования
- •Способ градиента
- •14.2 Системы с эталонной моделью. Алгоритмы идентификации Беспоисковые адаптивные системы управления
- •Идентификация и модель для получения оценки
- •Модель для получения оценки
Решетчатые функции и z-преобразование
При рассмотрении разностных уравнений важную роль играет z-преобразование. Но прежде чем приступить к изучению этого преобразования, познакомимся с классом дискретных функций, называемых решетчатыми функциями.
Решетчатые
функции. Дискретная функция
x(t)
по определению есть функция, которая
определена в дискретные моменты времени
t = lT (l =
0,1,
2,...).
Далее дискретную функцию будем записывать
в виде
х[lТ],
используя
t
как непрерывную переменную. В теории
дискретных систем рассматривают особый
тип дискретных функций, называемых
решетчатыми функциями.
Решетчатая функция
х[lТ]
характеризуется тем, что она определяется
непрерывной функцией (функцией
непрерывного аргумента)
x(t)
и принимает ее значения в моменты
t = lT (l =
0,1,
2, ...).
Кроме того, используется
смещенная решетчатая функция
![]() ,
которая принимает значения непрерывной
функции в моменты
,
которая принимает значения непрерывной
функции в моменты![]() (l = 0,1,2,...).
Поэтому когда говорят о решетчатой и
смещенной решетчатой функциях,
предполагают, что существует непрерывная
функция, которая определяет эти функции.
(l = 0,1,2,...).
Поэтому когда говорят о решетчатой и
смещенной решетчатой функциях,
предполагают, что существует непрерывная
функция, которая определяет эти функции.
Определение z-преобразования
z-преобразованием, или преобразованием Лорана, называется соотношение
 (12.1.17)
(12.1.17)
ставящее в соответствие дискретной функции х[1Т] функцию комплексного переменного X*(z). При этом х[1Т] называют оригиналом, a X*(z) — изображением или z-изображением. Оригинал и его изображение обозначают одноименными буквами: оригинал — строчной буквой, а изображение — прописной буквой со звездочкой.
z-преобразование также условно записывают в виде
X*(z) = Z{x[lT]},
а обратное z-преобразование — в виде
x[1Т] = Z-1{X*(z)}.
Предполагается, что в z-преобразовании (12.1.17) дискретная функция обладает следующими свойствами:
1)
существуют положительные числа М и q
такие, что
![]() при
любых
при
любых
![]() ;
;
2) х[lТ] = 0 при всех l < 0.
Свойство 1) необходимо для существования области сходимости ряда в правой части (12.1.17), а свойство 2) используется при выводе некоторых свойств z-преобразования. Функции, удовлетворяющие указанным двум свойствам, называют функциями-оригиналами.
z-преобразование
от смещенной решетчатой функции
![]() ,
т.е. соотношение
,
т.е. соотношение
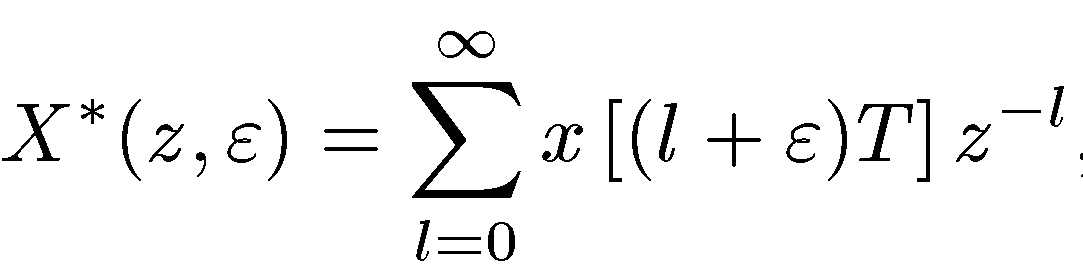 называют
модифицированным z-преобразованием.
Модифицированное z-преобразование
также записывают в виде
называют
модифицированным z-преобразованием.
Модифицированное z-преобразование
также записывают в виде
![]()
Функцию
![]() называют
z-изображением
смещенной решетчатой функции
называют
z-изображением
смещенной решетчатой функции
![]() или
модифицированным z-изображением
решетчатой
функции
х[lТ].
или
модифицированным z-изображением
решетчатой
функции
х[lТ].
Пример
12.1.1. Определить z-изображение
единичной решетчатой функции
х[lТ]
= 1[IT]
и смещенной решетчатой функции
![]()
![]() .
.
Решение.
Так как при всех
![]()
![]() ,
то
,
то
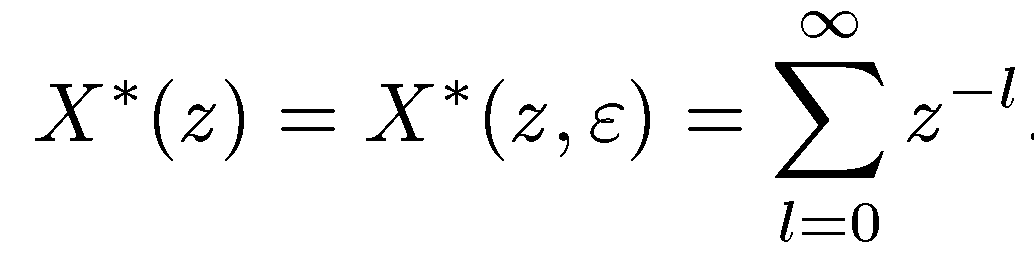
По формуле суммы бесконечно убывающей геометрической прогрессии имеем
![]() .
.
Основные свойства z-преобразования
Так
как
z-преобразование
от
х[lТ]
можно рассматривать как частный случай
модифицированного z-преобразования
при
![]() ,
то рассмотрим свойства модифицированного
я-преобразования. Доказательства
приводятся в конце, после рассмотрения
всех свойств.
,
то рассмотрим свойства модифицированного
я-преобразования. Доказательства
приводятся в конце, после рассмотрения
всех свойств.
1°. Линейность. Модифицированное z-преобразование от линейной комбинации дискретных функций равно линейной комбинации их модифицированных z-преобразований:
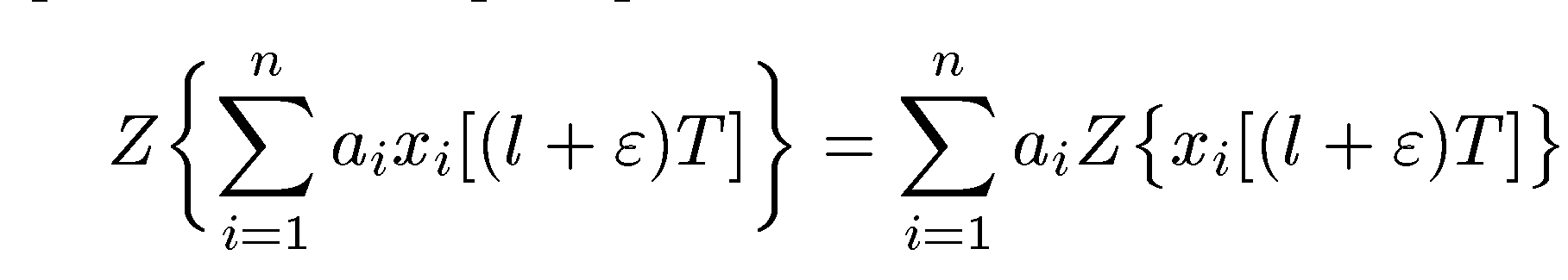 12.1.18
12.1.18
Здесь ai (i = 1, 2,..., п) — константы.
2°. Теорема запаздывания. Модифицированное z-преобразование от функции с запаздывающим аргументом х[(l — т)Т] определяется следующим образом:
![]() . (12.1.19)
. (12.1.19)
3°. Теорема опережения. Модифицированное z-преобразование от функции с опережающим аргументом x[(l + т)Т] определяется следующим образом:
![]() Если
Если
![]() (начальные условия нулевые), то
(начальные условия нулевые), то
![]() . (12.1.20)
. (12.1.20)
4°.
Умножение оригинала на
![]() .
z-преобразование
от произведения
.
z-преобразование
от произведения
![]() определяется следующим образом:
определяется следующим образом:
![]() . (12.1.21)
. (12.1.21)
При
![]() имеем
имеем
![]() (12.1.22)
(12.1.22)
Пользуясь
полученным свойством, найдем обычное
и модифицированное z-изображения
функции
![]() .
.
Модифицированное z-изображение для единичной функции (см. формулу (12.1.23)) имеет вид
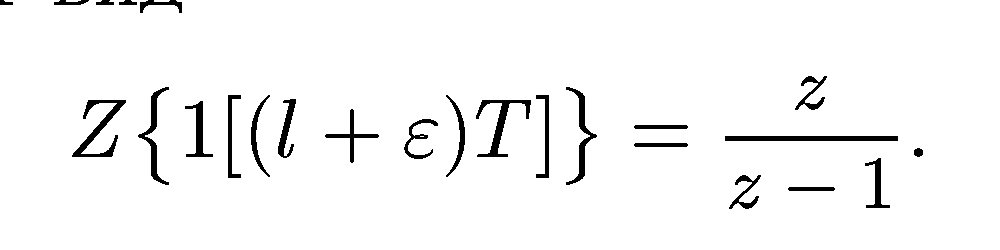
Поэтому
если в (12.1.21) положим
![]() ,
то получим
,
то получим
![]() (12.1.23)
(12.1.23)
Отсюда
при
![]() имеем
имеем
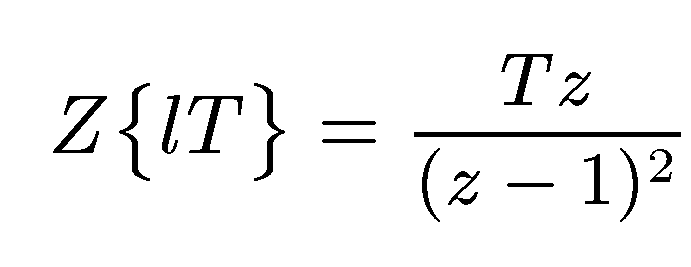 (12.1.24)
(12.1.24)
5°.
Умножение оригинала на
![]() .
z-преобразование
от произведения
.
z-преобразование
от произведения
![]() определяется следующим образом:
определяется следующим образом:
![]() . (12.1.25)
. (12.1.25)
При
![]() имеем
имеем
![]() . (12.1.26)
. (12.1.26)
Найдем
обычное и модифицированное z-изображения
функции
![]() .
Положив в (12.1.25)
.
Положив в (12.1.25)
![]() и
а
= е, получим
и
а
= е, получим![]()
При
![]() имеем
имеем
![]() (12.1.26)
(12.1.26)
6°.
Теорема о свертке.
Произведение изображений
![]() и
и
![]() равно z-преобразованию
от свертки их оригиналов
равно z-преобразованию
от свертки их оригиналов
![]() и
:
и
:
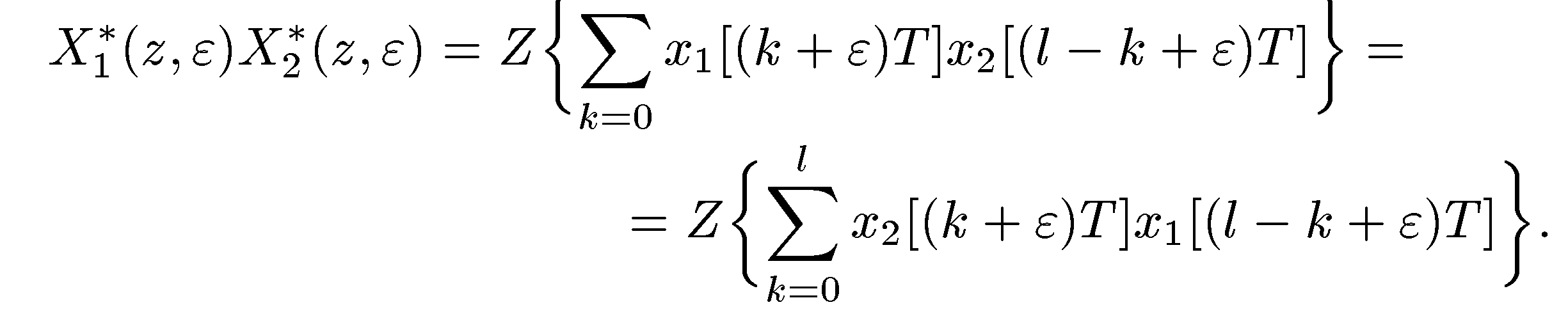 (12.1.27)
(12.1.27)
При
![]() имеем
имеем
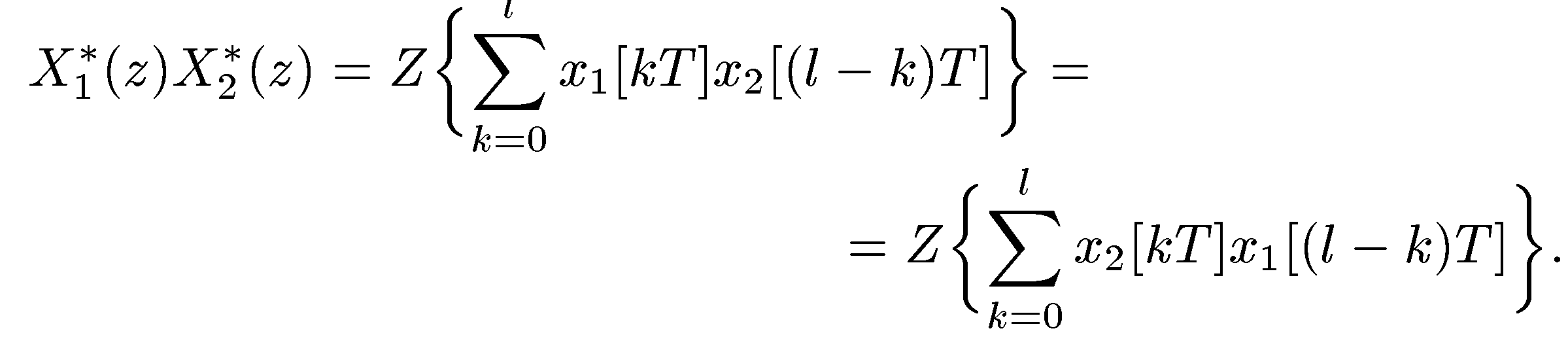 .
(12.1.28)
.
(12.1.28)
'
7°. Теоремы о граничных значениях. Начальное значение решетчатой функции х[lТ] по ее обычному и модифицированному z-изображению определяется следующим образом:
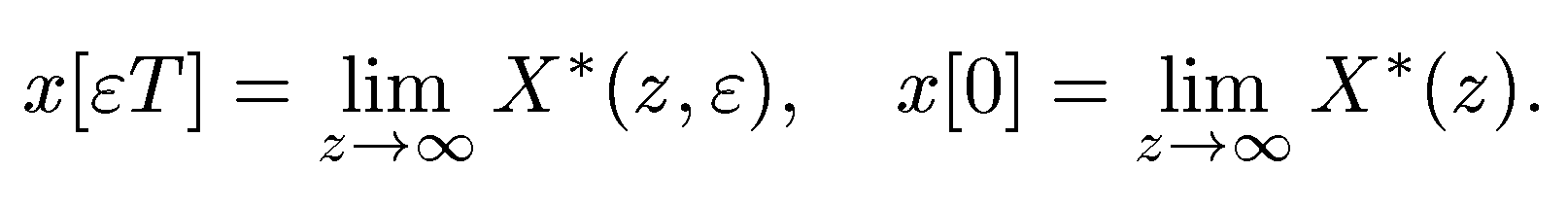 . (12.1.29)
. (12.1.29)
Предел
![]() при условии, что он существует,
определяется следующим образом:
при условии, что он существует,
определяется следующим образом:
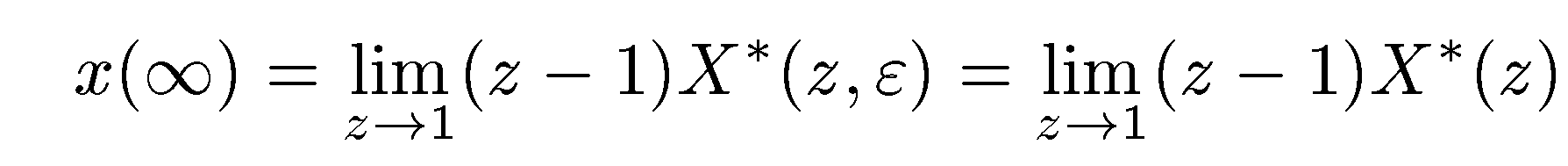 .
(12.1.30)
.
(12.1.30)
z-изображения основных функций
В табл. 12.1.1 и табл. 12.1.2 представлены соответственно обычные и модифицированные я-изображения основных решетчатых функций. Как отмечалось, решетчатая функция х[lТ] получается путем квантования (дискретизации) по времени непрерывной функции x(t). В дальнейшем потребуется вычислять z-изображение решетчатой функции по известному изображению Лапласа X(s) непрерывной функции x(t). И при этом чтобы избежать этапов вычисления x(t) путем обратного преобразования Лапласа и дискретизации, в указанных таблицах в первом столбце приведены изображения Лапласа соответствующих непрерывных функций.
Рассмотрим вывод формул, приведенных в табл. 12.1.1 и табл. 12.1.2. И так как формулы для обычных z-изображений получаются из формул для модифицированных z-изображений при l= 0, ограничимся выводом формул, приведенных в табл. 12.1.2.
Таблица 12.1.1. z-изображения
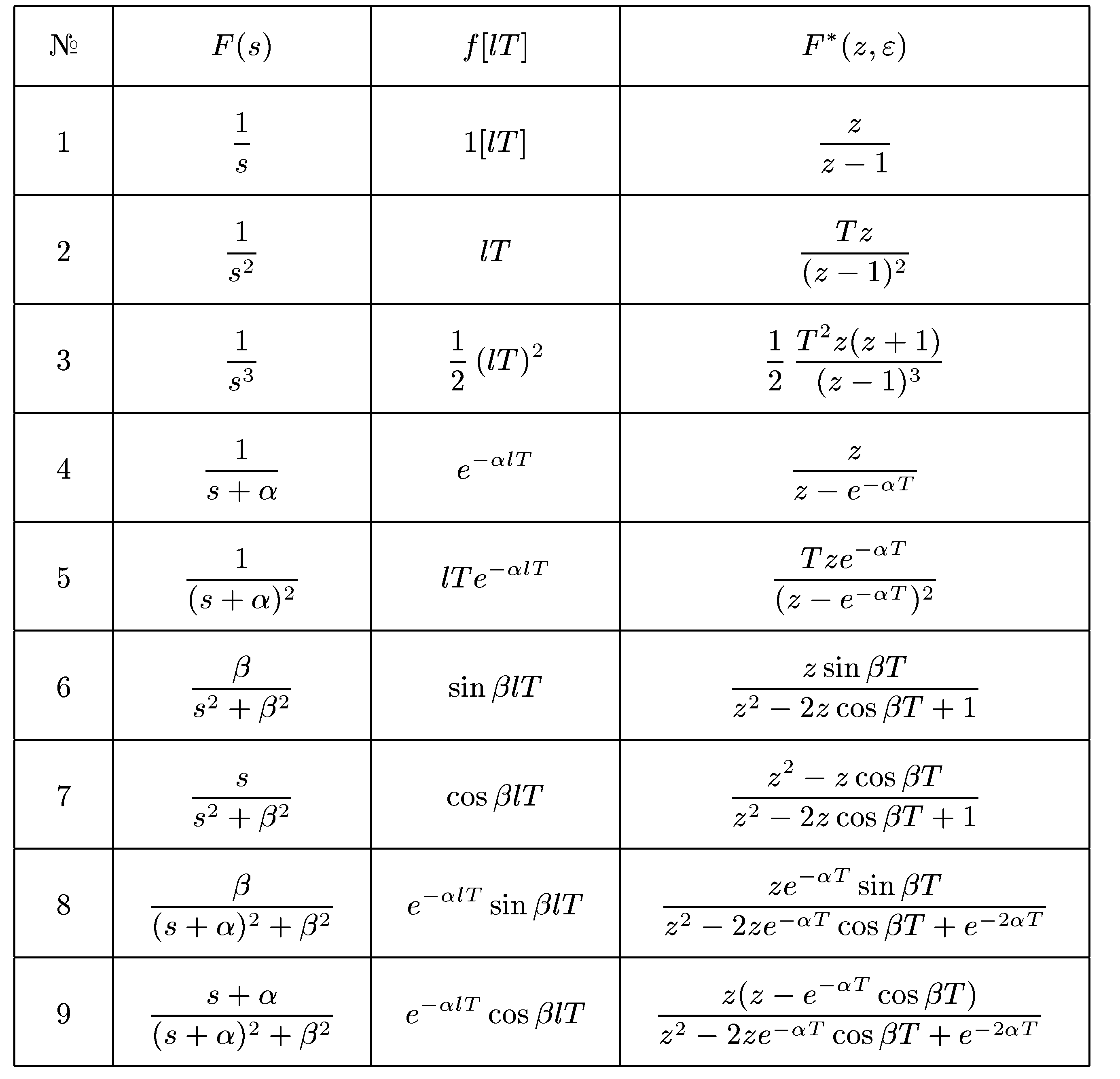
Таблица 12.1.2. Модифицированные z-изображения