Раздел 8. Косвенные критерии качества

8.1 Косвенные критерии качества. Корневые критерии качества — степень устойчивости и степень колебательности

К корневым оценкам относятся степень устойчивости и степень колебательности.

Степень устойчивости

Степень устойчивости численно равна абсолютному значению действительной части ближайшего к мнимой оси корня (рис. 8.1.1).

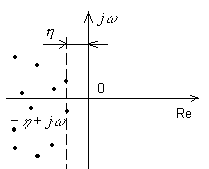
Рисунок 8.1.1 - К определению степени устойчивости

Система обладает достаточным запасом устойчивости, если достаточно велико. Запишем уравнение переходного процесса (движения системы):

(8.1.1)

Если , то

, (8.1.2)

где .

Степень устойчивости характеризует интенсивность затухания переходного процесса (рис. 8.1.2).

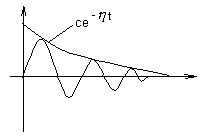
Рисунок 8.1.2 - Интерпретация степени устойчивости

Наименьшему по абсолютной величине корню соответствует наиболее медленно затухающая составляющая переходного процесса.

Связь степени устойчивости с быстродействием

Пусть за время tp составляющая переходного процесса от значения h1(0)=C1 уменьшилась в m раз (рис.8.1.3).

; (8.1.3)

; (8.1.4)

; (8.1.5)

. (8.1.6)

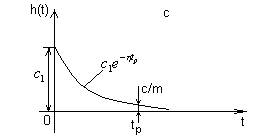
Рисунок 8.1.3 К связи степени устойчивости с быстродействием

Увеличению времени tp при m=const соответствует уменьшение . Чем больше , тем быстрее затухает процесс.

Степень колебательности

Из начала координат проведём лучи через два комплексно сопряжённых корня так, чтобы все остальные корни оказались между этими лучами (рис. 8.1.4).

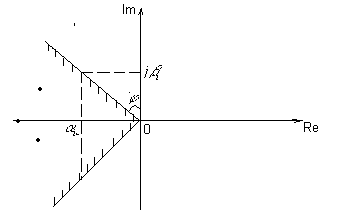
Рисунок 8.1.4 - К определению степени колебательности

Степенью колебательности называется отношение

. (8.1.7)

Из рис. 8.1.4 следует, что

. (8.1.8)

Чем больше m, тем быстрее затухает колебательный процесс. Степень колебательности характеризует запас устойчивости системы.

Если на систему накладывается требование , то это означает, что все корни характеристического уравнения системы должны находиться внутри заштрихованного сектора.

Для системы второго порядка с двумя комплексными сопряженными корнями уравнение движения

. (8.1.9)

Найдём связь степени колебательности и степени затухания. В выражение степени затухания (8.1.9) подставим:

, (8.1.10)

, (8.1.11)

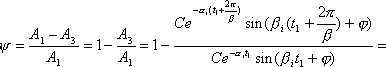
. (8.1.12)

Заметим, что для систем более высокого (>2) порядка соотношение (8.1.12) является приближённым. Степень его достоверности повышается в тех случаях, когда пара комплексных сопряжённых корней, определяющая m, имеет вещественную часть, значительно отличающуюся от вещественной части остальных корней.

8.2 АНАЛИЗ СТЕПЕНИ УСТОЙЧИВОСТИ И СТЕПЕНИ КОЛЕБАТЕЛЬНОСТИ МЕТОДОМ СМЕЩЕННОГО ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ ЗАДАННОЙ СТЕПЕНИ УСТОЙЧИВОСТИ И СТЕПЕНИ КОЛЕБАТЕЛЬНОСТИ

Частотные критерии качества. Запас устойчивости по модулю и по фазе. Показатель колебательности М и ME. Интегральные критерии качества, методы вычисления

Анализ степени устойчивости и степени колебательности

Простейшей корневой оценкой качества является степень устойчивости — расстояние η от мнимой оси до ближайшего корня на плоскости корней λ характеристиче­ского уравнения замкнутой системы (рис. 8.2.1). Если ближайшим является вещественный корень (рис. 8.2.1, а), то ему соответствует апериодическая составляющая решения для переходного процесса

(апериодическая степень устойчивости η). Время ее затухания

при ∆=5% (8.2.1)

х арактеризует общую длительность переходного процесса, так как все члены решения, соответствующие остальным корням, затухают быстрее.

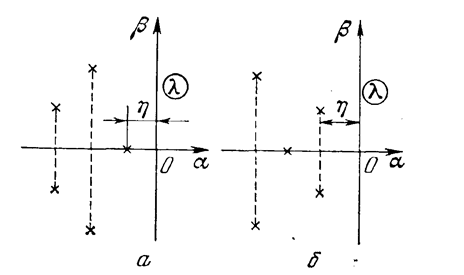
Рисунок 8.2.1 – Корневой степень устойчивости

Если же ближайшей к мнимой оси окажется пара комплексных корней (рис. 8.2.1, б), то доминирующая составляющая решения для переходного процесса

(8.2.2)

будет колебательной (колебательная степень устойчивости η), причем оценка длительности переходного процесса t_п остается прежней (8.2.2).

Определяется величина степени устойчивости следующим образом. Вводится новая комплексная переменная z = λ + η (рис. 8.2.2). Тогда на плоскости z мнимая ось β΄ пройдет через ближайшие корни, т. е. составленное относительно z характеристическое уравнение должно удовлетворять условию нахождения на границе устойчивости.

Таким образом, если задано характеристическое уравнение

(8.2.3)

то подставив λ = z — η , а именно

(8.2.4)

получим новое уравнение, которое называется смещенным, в виде

(8.2.5)

где коэффициенты A₁, A₂ , ..., A_n являются функциями η. Их можно вычислить следующим образом:

(8.2.6)

что вытекает из представления выражения (8.2.5) как результата разложения функции D(λ) (8.2.4) при λ = z - η в ряд Тейлора.

Затем к уравнению (8.2.5) применяется условие границ устойчивости, например, по Гурвицу

(8.2.7)

откуда и определяется величина η. Ниже будет дана диаграмма степени устойчивости для системы третьего порядка.

Рисунок 8.2.2 -

Колебательность переходного процесса определяется величиной

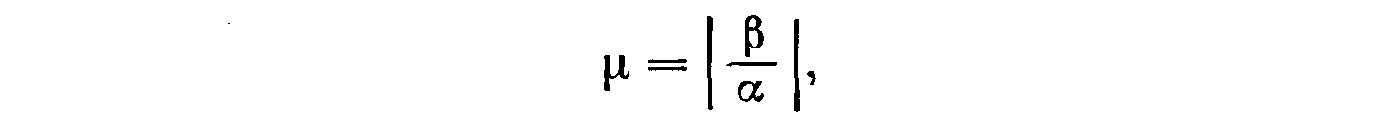
где α и β — вещественная и мнимая части корней характеристического уравнения. Именно эта величина характеризует быстроту затухания колебаний за каждый период. В самом деле, паре комплексных корней λ_{1 , 2} = -|α| ± jβ соответствует составляющая решения переходного процесса

Период колебаний равен

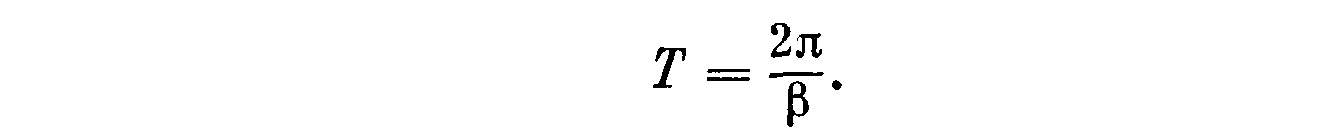
Через один период амплитуда C₁ e ^{– | α | t} уменьшается до величины

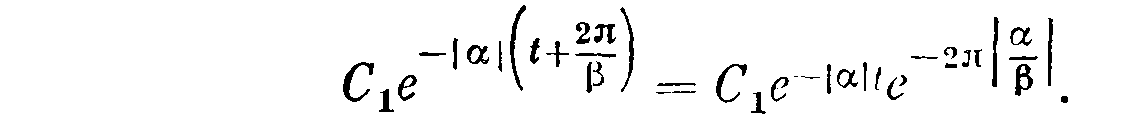
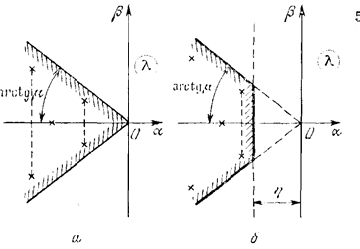
Рисунок 8.2.3 -

Следовательно, чем больше величина , названная колебательностью, тем слабое будет затухание колебаний в переходном процессе. Линия μ = const образует центральный угол (рис. 8.2.3, а) на комплексной плоскости.

Суммарное требование определенных значений степени устойчивости η и колебательности μ приводит к области, изображенной на рис. 8.2.3, б, внутри которой должны лежать все корни характеристического уравнения замкнутой системы.

Далее необходимо иметь в виду, что для определения качества переходного процесса при единичном скачке внешнего воздействия существенны не только корни характеристического уравнения, т. е. полюса, по также и нули передаточной функции замкнутой системы Ф(s). В самом деле, как мы знаем,

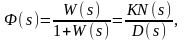
(8.2.8)

Воспользуемся формулой (8.2.8), разложив многочлен N(s_i) на множители

(8.2.9)

где s_i = λ_i полюса Ф(s), т. е. корни характеристического уравнения D(λ) = 0; через N₁, N₂, ..., N_m обозначены нули (корпи) многочлена N(s).

Отсюда видно, что амплитуды отклонений в переходном процессе, стоящие под знаком суммы, будут тем меньше, чем ближе расположены нули N_j к полюсам s_i т. е. корпи многочлена N(s) к корням характеристического уравнения. Именно в этом случае величины (s_i — N_j) будут малы. Это соответствует, например, схеме рис. 5.2.4, где нули обозначены кружочками. Заметим, что нули для замкнутой системы совпадают с нулями разомкнутой цепи W(s), так как

а полюса Ф(s) и W(s) существенно отличаются друг от друга.

Итак, для уменьшения амплитуд отклонений в переходном процессе желательно, чтобы нули передаточной функции замкнутой си­стемы Ф(s) располагались вблизи ее полюсов.

Примером корневых оценок качества переходного процесса в системах третьего порядка является диаграмма Вышнеградского (дана в его работе 1876 г., положившей начало развитию теории автоматического регулирования).

Характеристическое уравнение системы третьего порядка

(8.2.10)

приводится к нормированному виду

(8.2.11)

где , 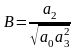(8.2.12)

Параметры Вышнеградского А и В представляют, следовательно, определенные комбинации реальных параметров системы, входящих в коэффициенты характеристиче­ского уравнения.

На плоскости параметров А, В граница устойчивости выразится зависимостью АВ = 1 (гипербола). Область устойчивости АВ > 1 разбивается на три подобласти (рис. 8.2.5) с различным расположением корней характеристического уравнения и соответственно — очертаний переходного процесса. При этом граничные линии СЕ и

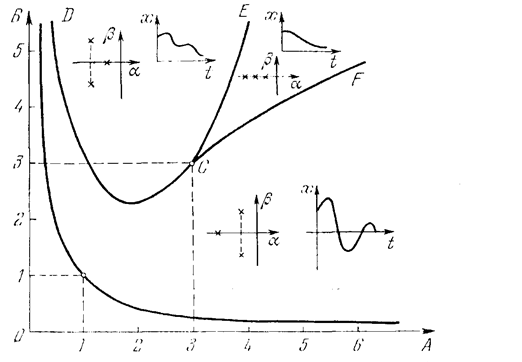
Рисунок 8.2.5 -

CF находятся приравниванием нулю дискриминанта формулы Кардана (решения кубического уравнения) в виде

а линия CD — из равенства вещественных частей всех корней —

В точке С (3; 3) все три корня вещественны и равны —1.

Позднее на диаграмму Вышнеградского были нанесены линии равных значений степени устойчивости η и линии равных значений колебательности μ.

При определении степени устойчивости смещенное уравнение для нормированного характеристического уравнения (8.2.12) будет

где согласно формулам (8.2.5)

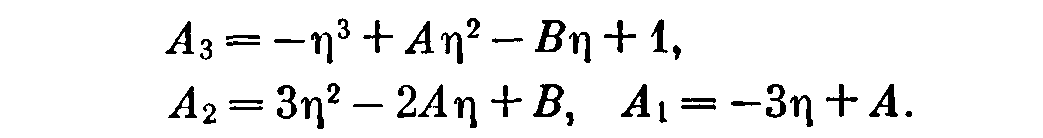
Два условия (8.2.6) принимают соответственно вид

(8.2.13)

(8.2.14)

Полагая η = const, нанесем линии равных значений η на плоскость параметров Вышнеградского А, В. При этом согласно уравнению (8.2.13) получим для разных конкрет­ных значений η прямые линии, а согласно уравнениям (8.2.14) — кривые (рис. 8.2.6).

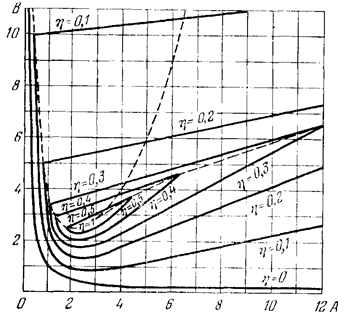
Рисунок 8.2.6 -

Для определения линий равных значений величины колебательности μ системы третьего порядка (8.2.6), когда корни его

имея в виду, что μ = β₁ /α₁ , по формулам Виета запишем

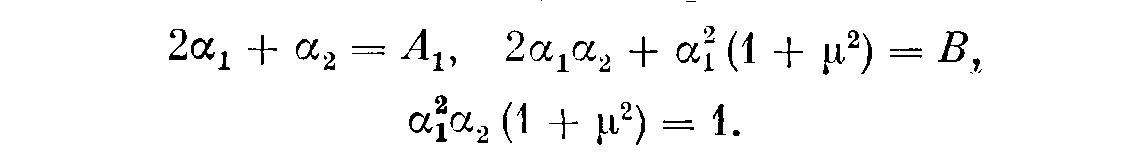
Исключая α₁ и α₂, обозначив x = 1 + μ², получим уравнение

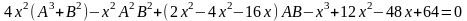(8.2.15)

которое позволяет построить на поле диаграммы Вышнеградского АВ линии равных значений μ = (рис. 8.2.7) в областях, где имеются комплексные корни. Если нам требуется в системе третьего порядка выбрать параметры так, чтобы получить заданное качество

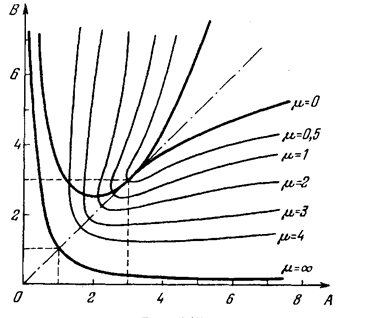
Рисунок 8.2.7 -

переходного процесса по показателям η и μ, мы выбираем на рис. 8.2.6 и 8.2.7 соответствующую точку. Найдя таким образом значения А и B, пользуемся затем фор­мулами (8.2.13) для подбора параметров системы (8.2.12).