10.2 Анализ нелинейных систем на фазовой плоскости. Классификация особых точек. Автоколебания. Метод точечных преобразований

При исследованиях нелинейных систем широко используется метод фазового пространства, относящийся к группе графоаналитических методов, описывающих поведение систем при помощи наглядных геометрических представлений - фазовых портретов. Применительно к линейным системам этот метод рассмотрен в разделе 6.3.

Основные понятия

Основным понятием метода является понятие фазового пространства, под которым понимается пространство, в котором прямоугольными координатами точки являются величины, определяющие мгновенное состояние системы, называемые фазовыми координатами.

Метод фазового пространства применим как для линейных, так и для нелинейных систем. Последние в общем случае описываются системой нелинейных дифференциальных уравнений вида:

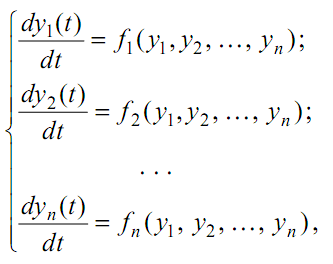(10.2.1)

,где y₁ , y₂ , …, y _n - фазовые координаты: t - время;f₁ , f₂, …, f _n - нелинейные функции.

Фазовые координаты y₁,y2,…,y_n могут иметь любой физический смысл - температура, концентрация и др., но обычно в качестве них выбирают выходную переменную и ее (n−1) производную, т.е.

y₁₍t)=y(t), y₂₍t) =y′( t),…,y_n( t)=y⁽ⁿ⁻¹⁾( t)

Наибольшее распространение метод фазового пространства получил при исследовании систем второго порядка. В этом случае фазовым пространством является плоскость. Система дифференциальных уравнений (10.2.1) для системы второго порядка запишется в виде

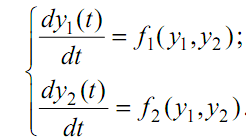(10.2.2)

Из этой системы получают уравнение, описывающее фазовый портрет. Для этого необходимо исключить из рассмотрения время, в результате чего получают следующее

(10.2.3)

решение которого дает семейство интегральных кривых на фазовой плоскости, являющихся фазовыми траекториями системы.

Фазовые портреты нелинейных систем

Фазовые портреты нелинейных систем второго порядка определяются решением дифференциального уравнения (10.2.3), которое в данном случае является нелинейным, что и обуславливает характерные особенности этих траекторий.

^{Линейная система имеет единственное состоя}ние равновесия, определяемое (10.2.3), и характер особой точки полностью определяет поведение системы при любых отклонениях от состояния равновесия. В нелинейной системе состояний равновесия может быть много, следовательно и особых точек также много, но их характер определяет поведение фазовых траекторий только вблизи них. Так, на рис. 10.2.1 изображен типичный фазовый портрет нелинейной системы.

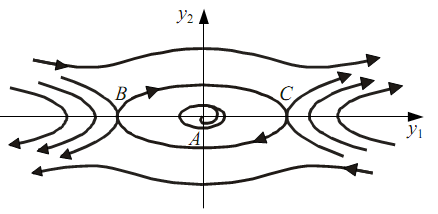
Рисунок 10.2.1 - Фазовый портрет нелинейной системы

Эта система имеет три состояния равновесия в точках А, В, С. Причем точка А является особой точкой типа "центр", а В и С - типа "седло". При рассмотрении свободных движений их амплитуда может вырасти до определенного предела и оставаться далее постоянной, а не расходиться. На фазовой плоскости помимо особых точек фазовый портрет может содержать особые линии, одной из которых является особая траектория - изолированная замкнутая кривая, называемая предельным циклом (рис. 10.2.2). Фазовые траектории могут асимптотически приближаться к предельному циклу - "наматываться" (рис. 10.2.2, а) и "сматываться", уходя в бесконечность (рис. 10.2.2, б).

Предельным циклам соответствуют периодические процессы, в окрестности которых имеют место колебательные процессы (рис. 10.2.3), т.е. предельному циклу соответствует режим автоколебаний в системе.

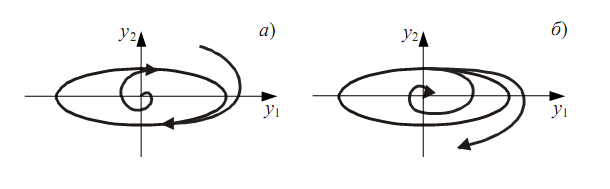
Рисунок 10.2.2 - Особые фазовые траектории − предельный цикл:а - устойчивый; б - неустойчивый

Р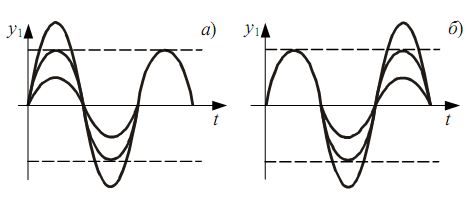 исунок 10.2.3 ПЕРЕХОДНЫЕ ПРОЦЕССЫ:

А - ПРИ УСТОЙЧИВОМ ПРЕДЕЛЬНОМ ЦИКЛЕ; Б - ПРИ НЕУСТОЙЧИВОМ ПРЕДЕЛЬНОМ ЦИКЛЕ

Предельные циклы могут быть устойчивыми и неустойчивыми, и соответственно автоколебания - устойчивыми и неустойчивыми. Предельный цикл называется устойчивым, если фазовые траектории снаружи и изнутри "наматываются на него" (рис. 10.2.2, а, 10.2.3, а). В такой системе обязательно будет наблюдаться автоколебательный режим.

Предельный цикл называется неустойчивым, если фазовые траектории удаляются от него с обеих сторон, т.е. "сматываются" (рис. 10.2.2, б, 10.2.3, б).

Если начальные условия таковы, что изображающая точка находится внутри предельного цикла, представленного на рис. 10.2.2, а, то она будет двигаться по фазовой траектории к нему, система ведет себя, как неустойчивая система, особая точка - начало координат является неустойчивым фокусом. Если же в начальный момент времени изображающая точка находится снаружи предельного цикла, то она движется по фазовой траектории, приближаясь к нему, система ведет себя как устойчивая система. В этом случае говорят, что рассматриваемая система неустойчива "в малом", устойчива "в большом" и режим автоколебаний устойчивый.

Если рассматривать те же самые начальные условия, но для случая, представленного на рис. 10.2.2, б, то говорят, что система устойчива "в малом" (особая точка - устойчивый фокус), неустойчива "в большом", режим автоколебаний неустойчивый.

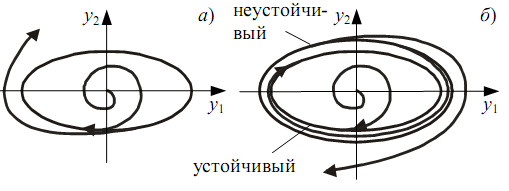
Рисунок 10.2.4 - Фазовый портрет системы:

а - полуустойчивый предельный цикл; б - с двумя предельными циклами

Если начальные условия таковы, что одна фазовая траектория "наматывается" на предельный цикл, а другая - "сматывается", то система является неустойчивой и "в малом", и "в большом". В этом случае предельный цикл и соответственно режим автоколебаний называется полуустойчивым (рис. 10.2.4, а). Система может иметь не один, а несколько предельных циклов. Система, фазовый портрет которой изображен на рис. 10.2.4, б, имеет два предельных цикла, один из них - внутренний устойчивый, другой – внешний неустойчивый. Состояние равновесия одно и неустойчивое.

Другим видом особых линий, которые встречаются в нелинейных системах, являются сепаратрисы- кривые, разделяющие области фазового портрета с различным характером фазовых траекторий. Так, в линейных системах второго порядка при рассмотрении фазового портрета типа седло асимптоты гипербол y= ±ωy₁ , ω ² = a₀/a₂, a₁=0 и являются как раз сепаратрисами.

Типичный фазовый портрет нелинейной системы изображен на рис. 10.2.5. Здесь имеются следующие особые точки: точка А - устойчивый фокус, точка В - неустойчивый узел и точка С - седло. В соответствии с этим сепаратрисы разделяют фазовый портрет на четыре области: 1 - затухающих колебаний, 2 - автоколебаний, 3 и 4 - неустойчивых апериодических процессов.

Р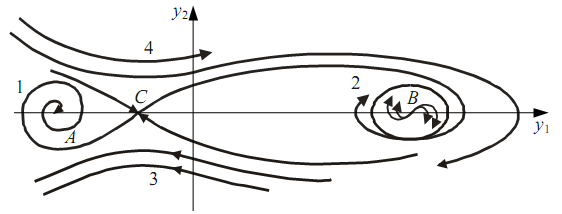 исунок 10.2.5 - Фазовый портрет нелинейной системы

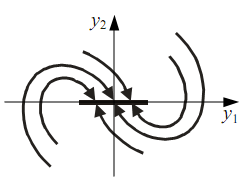
Рисунок 10.2.6 - Фазовый портрет с особой линией

Нелинейные системы с элементами, имеющими зону нечувствительности или сухое трение, имеют не один стационарный режим, а целую область, что на фазовой плоскости выражается "вытягиванием" особой точки в особую линию (рис. 10.2.6).

В заключение следует сказать, что если известен фазовый портрет, то о системе известно все.