Метод Акульшина

Рассмотрим приближенный метод построения переходного процесса, предложенный Акульшиным. Основное достоинство метода состоит в возможности программирования на ЭВМ.

Сущность метода заключается в следующем. Пусть на вход системы подаются прямоугольные колебания (рис. 7.1.3).

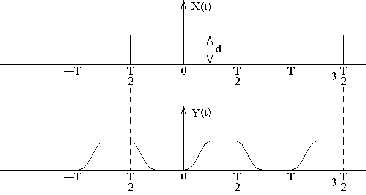
Рисунок 7.1.3 - К расчету переходного процесса методом Акульшина

Период колебаний Т выбирается достаточно большим, так, чтобы переходный процесс в системе заканчивался за половину периода. В этом случае выходная величина в установившемся режиме будет определять последовательность переходных кривых (рис. 7.1.3).

Реакция на ступенчатое воздействие будет практически совпадать с выходной величиной y(t) на первом полупериоде. Входные прямоугольные колебания могут быть разложены в ряд Фурье:

, (7.1.4)

где d – амплитуда входных колебанй;

T – период колебаний;

k = 1, 3, 5, ...

Реакция линейной системы на гармонический сигнал вида

(7.1.5)

определяется формулой

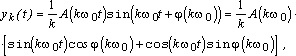(7.1.6)

где A(w), j(w) – амплитудно-частотная и фазо-частотная характеристики системы.

Учитывая, что

получим:

, (7.1.7)

где Re(w), Jm(w) – вещественная и мнимая частотные характеристики системы.

Учитывая, что реакция системы на постоянную составляющую d/2 равна

, (7.1.8)

получим ( используя принцип наложения ):

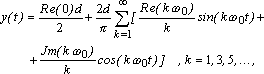(7.1.9)

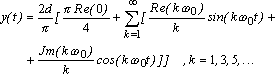(7.1.10)

Выражение (7.1.10) является исходным для построения переходного процесса в системе. При практических расчетах ограничиваются конечным числом членов ряда (7.1.10). Значения Y(t) вычисляют в равноотстоящие дискретные моменты времени t=it. Интервал разбиения t определяется по формуле:

. (7.1.11)

Если выбирать , то за полупериод колебаний получим не менее 12 точек переходной кривой. Расчетная формула для построения переходного процесса может быть записана следующим образом:

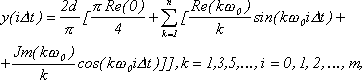(7.1.12)

где Re(w), Im(w) – вещественная и мнимая частотные характеристики замкнутой системы;

d – амплитуда входного сигнала.

Число гармоник n достаточно выбрать в пределах 15-30.

Сложной задачей является выбор величины (или периода T). Рекомендуется значение Т выбирать по формуле [6]:

, (7.1.13)

где – рабочая (резонансная) частота, соответствующая оптимальным настроечным параметрам.

Формула (7.1.13) получена из предположения, что переходный процесс в замкнутой АСР близок к процессу в колебательном звене, который заканчивается практически за 3.5 периода собственных колебаний. При таком выборе Т седьмая гармоника ряда (7.1.12) совпадает с резонансной. Для определения и Dt получаем формулы:

,

(7.1.14)

Значения Re(w) и Im(w) в (7.1.12) вычисляются по формулам:

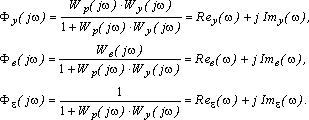
При этом

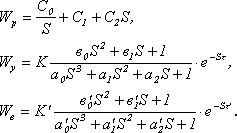
Исходными данными для расчета являются значения параметров и амплитуда входного воздействия d (удобно принять d=1 ). При вычислении ординат переходного процесса по (7.1.12) вычисляется одновременно и величина среднеквадратического отклонения по формуле (7.1.14).