7. Сравнение бесконечно малых величин
Пусть
и
– бесконечно малыми величинами при
.
Если
не обращается в нуль в некоторой
окрестности точки
и отношение
имеет конечный и отличный от нуля предел,
то
и
называются бесконечно
малыми величинами одного порядка.
Из данного определения следует, что и
бесконечно малая величина
не обращается в нуль в некоторой
окрестности точки
и отношение
имеет конечный и отличный от нуля предел:
.
Если и – бесконечно малые величины одного порядка и
,
то
и
называются эквивалентными
бесконечно малыми величинами
и обозначаются
при
.
Если и – бесконечно малые величины при и
,
то называется бесконечно малой величиной более высокого порядка чем . Если же
,
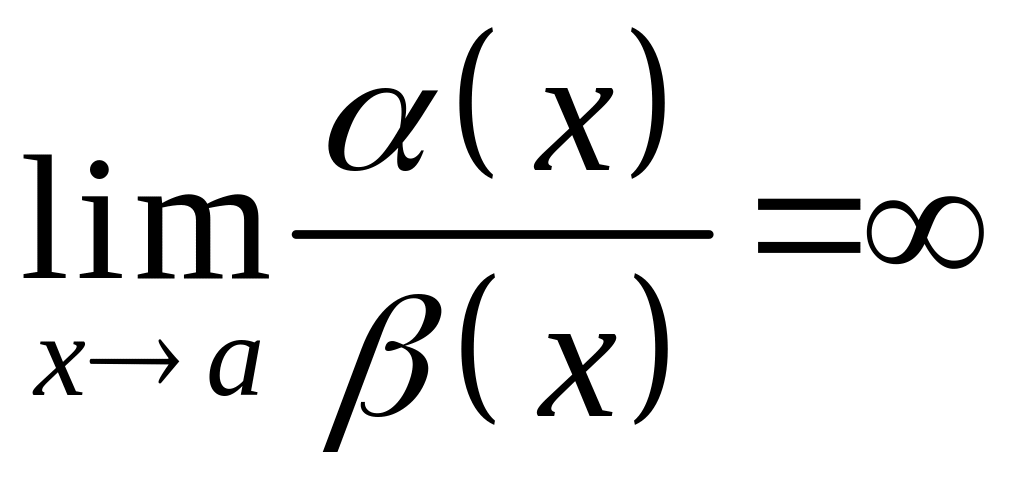то является бесконечно малой величиной более высокого порядка чем .
Бесконечно малая
величина
называется бесконечно
малой величиной k-го
порядка относительно бесконечно малой
величины
,
если
и
является бесконечно малыми величинами
одного порядка.
Теорема.
Для того эквивалентности бесконечно
малых величин
и
,
необходимо и достаточно, чтобы их
разность
являлась бесконечно малой величиной
более высокого порядка, чем
и чем
.
Если отношение бесконечно малых величин и не имеет предела и не стремится к бесконечности, то бесконечно малые величины и не сравнимы между собой.
8. Предельный переход в неравенствах
Теорема 1.
Пусть функции
и
определены в некоторой выколотой
окрестности
точки
и удовлетворяют неравенству
для всех
.
Если существуют пределы
и
,
(8.1)
тогда
.
Замечание.
Если вместо неравенства
выполняется строгое неравенство
,
то тем не менее при существовании
соотношений (8.1), утверждается нестрогое
неравенство
.
Теорема 2.
Пусть три функции
,
и
определены в некоторой выколотой
окрестности
точки
и удовлетворяют неравенствам
.
Если крайние функции
и
имеют равные пределы при
:
и
,
то средняя функция
имеет предел при
и справедливо равенство
.
9. Неопределенные выражения
В п. 4 мы изучали задачи вычисления пределов выражений
и, в предположении,
что функции
и
стремятся к конечным пределам (из
которых, в случае частного, предел
при
не должен был равняться нулю). В теоремах
2 – 5 приведены утверждения для вычисления
пределов этих выражений. Без рассмотрения
остались случаи, когда пределы функций
и
(один или оба) бесконечны или, если речь
идет о частном, когда предел знаменателя
равен нулю. Изучим эти случаи.
Рассмотрим частное
и предположим, что обе функции
и
одновременно стремятся к нулю:
и
.
Хотя нам известны пределы
и
,
но о пределе их отношения
,
не зная самых этих функций, никакого
утверждения мы сделать не можем.
Подтверждением этого являются примеры:
при
;
при
;
при
;
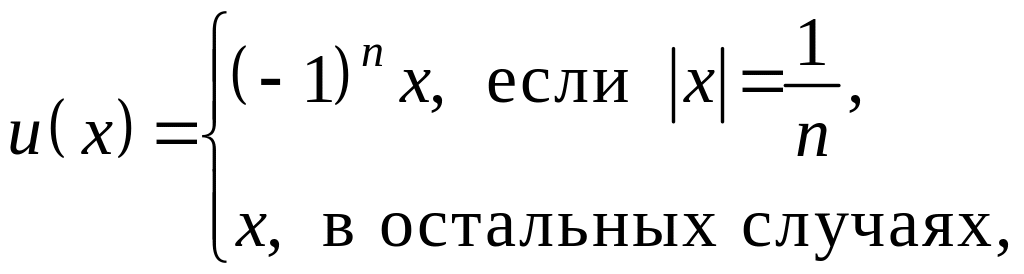
– нет предела.
В этом случае будем
говорить, что выражение
представляет неопределенность
вида
.
Если обе функции
и
одновременно стремятся к бесконечности:
и
,
то будем говорить, что выражение
представляет неопределенность
вида
.
Рассмотрим
произведение
и предположим, что одна из функций
стремятся к нулю, а другая – к бесконечности:
или
.
Здесь, как и в
случае неопределенности
,
можно привести соответствующие примеры.
для этого достаточно вместо функции
рассматривать функцию
.
В этом случае будем говорить, что
выражение
представляет неопределенность
вида
.
Рассмотрим сумму
и разность
.
Предположим, что обе функции являются
бесконечно большими функциями
противоположных знаков, в случае суммы
или бесконечно большими функциями
одинаковых знаков, в случае разности.
Рассмотрим примеры:
при
;
при
;
при
для любого вещественного числа .
при
,
а
не имеет предела при
.
В этом случае будем говорить, что
выражения
и
представляют неопределенность
вида
.
Рассмотрим функцию
.
Предположим, что функция
стремится к 1 при
:
,
а функция
– к бесконечности:
.
В этом случае будем говорить, что
выражение
представляет неопределенность
вида
.