§ 4. Характеристическое уравнение. Собственные векторы и собственные значения матрицы Аnn. Приведение матрицы Аnn к диагональному виду
Вектор-столбец
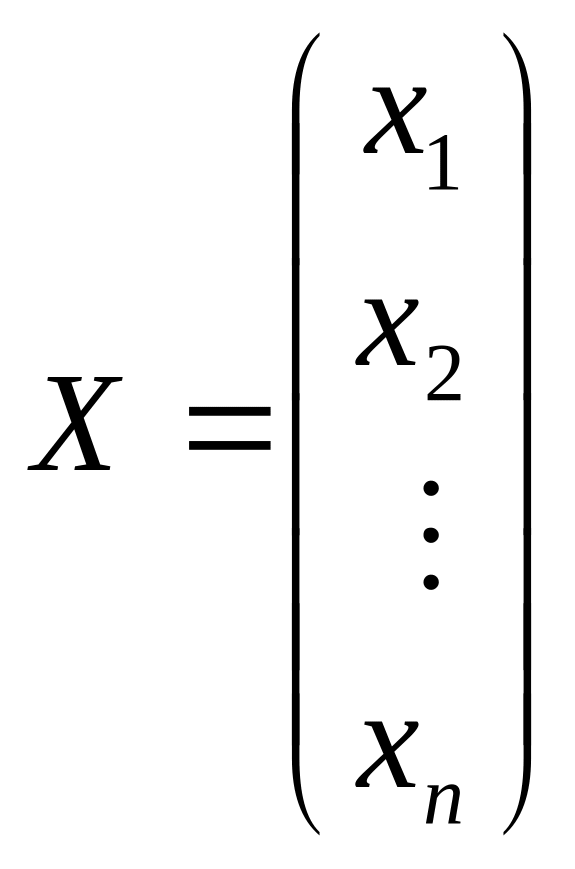
называется собственным вектором квадратной матрицы Аnn порядка n, соответствующим собственному значению , если он удовлетворяет матричному уравнению
,
. (4)
Так как
,
то из (4) получаем равенство вида:
или
.
(5)
Матрица
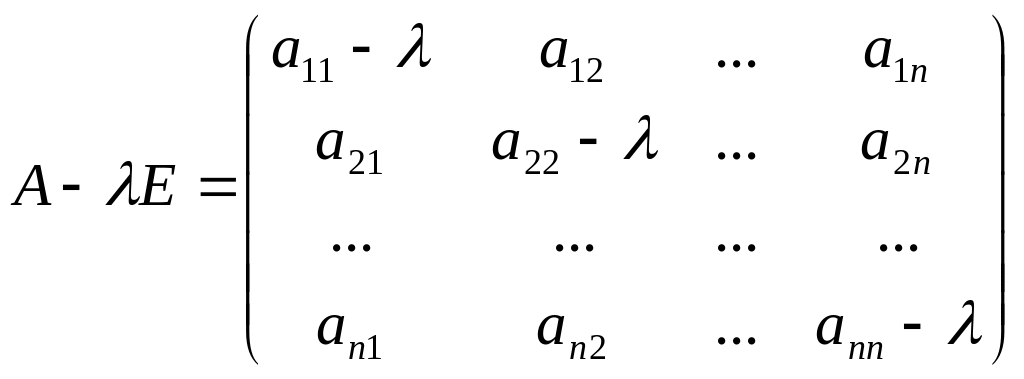(6)
уравнения (5) называется характеристической матрицей порядка n. Из (5) и (6) получаем ОСЛАУ вида:
. (7)
Система (7) имеет
ненулевое решение в силу теоремы 4 тогда
и только тогда, когда
n,
т.е.
. (8)
Из (7) и (8) получаем, что
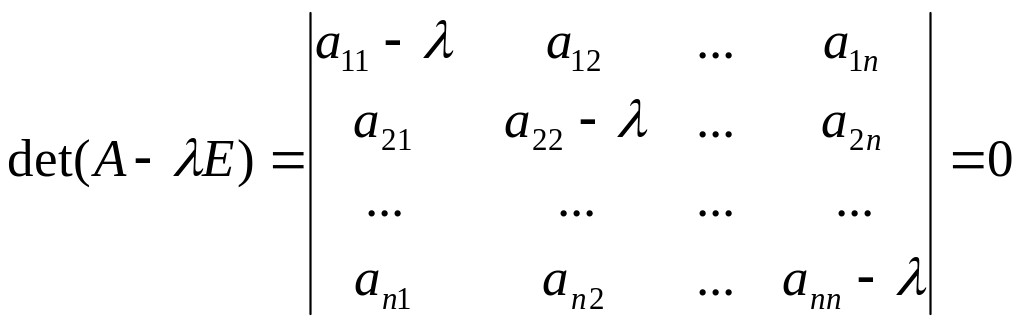. (9)
Определитель в левой части (8) называется характеристическим многочленом, а уравнение (9) n-ой степени относительно называется характеристическим уравнением:
.
Согласно основной
теоремы алгебры это уравнение имеет
ровно n
корней
,
некоторые из которых могут совпадать
и некоторые могут быть комплексно-сопряженными.
Если А
- симметрическая матрица, т.е.
,
то все
,
,
где
- множество вещественных чисел. Для
каждого
,
,
определяется из системы (7) при
собственный вектор
с точностью до постоянного множителя.
Совокупность
определяет базис из собственных векторов.
Пример. Найти собственные числа и собственные векторы матрицы
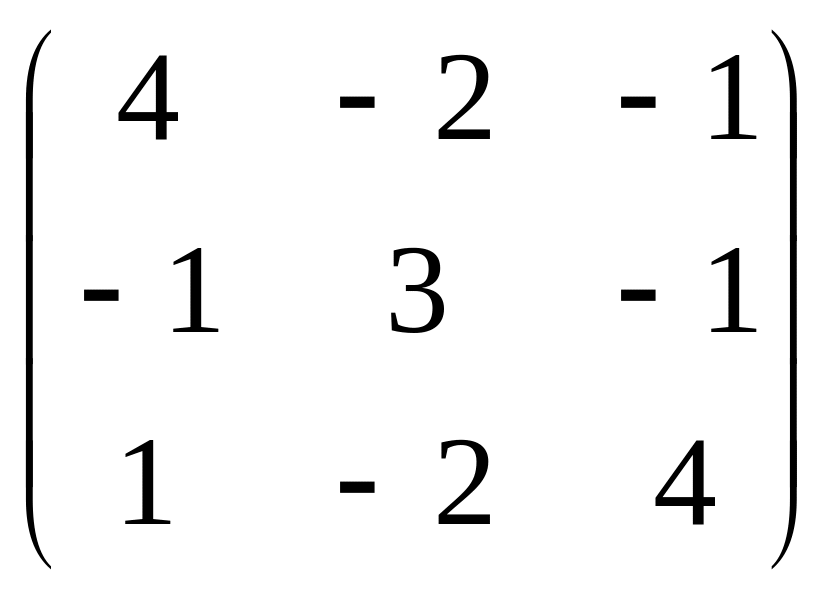
Решение. Запишем характеристическое уравнение:
=(
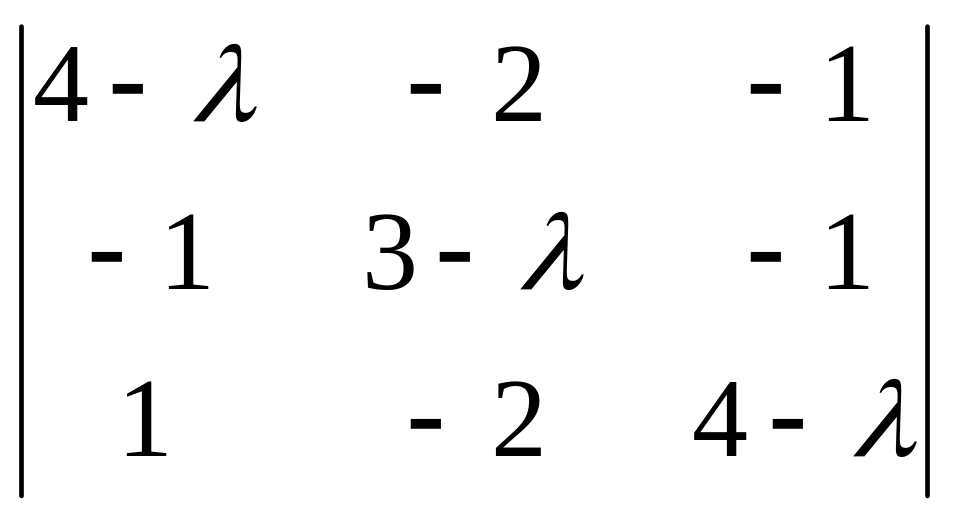4 -)[(3-)(4
-)-2]
+ 2[(
- 4)+1]- [2+-3]=
(16-8+2)(
3 -
) – 8+ 2
+2 -
+3 = 48 - 24
+32
-16
+82
- 3
+
-3 =- 3
+112
- 39
+45 =0 и, следовательно, 3
-112
+ 39
- 45=0.
По теореме Безу
находим множители свободного члена,
т. е. для 45. Один из них и будет корнем
данного уравнения (это 5). Разделим данное
уравнение на (-5).
Получим: (
- 5)( 2
- 6
+9)=0 . Применяя теорему Виета получим
равенство (
- 5) (
-3) (
-3)=0,из которого находим его корни
,
.
Для нахождения собственных векторов
и
рассмотрим ОСЛАУ вида (7):
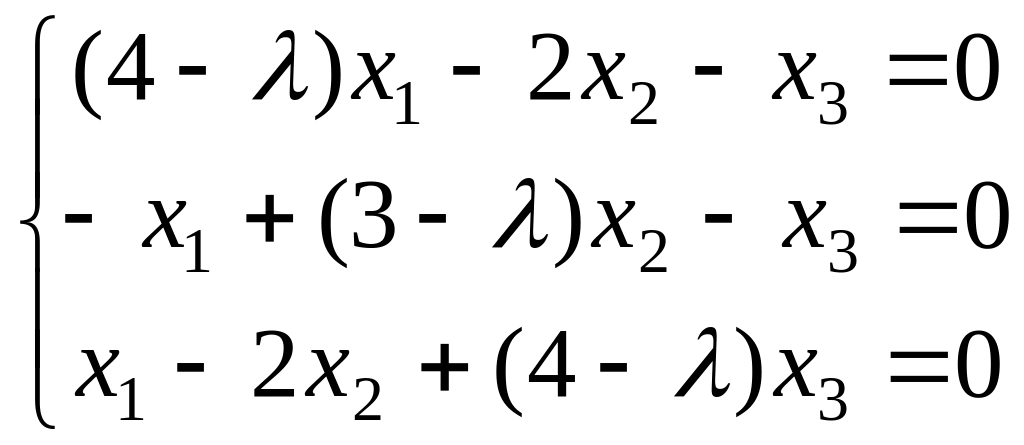
Пусть
=
.
Тогда получаем систему.
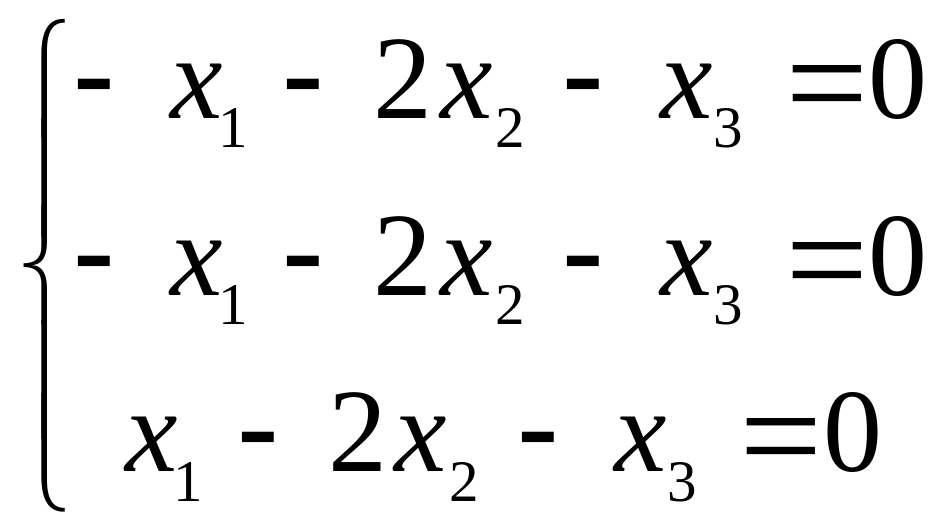или
Вычитая из первого уравнения этой системы второе получим:
.
Полагая
,
находим
,
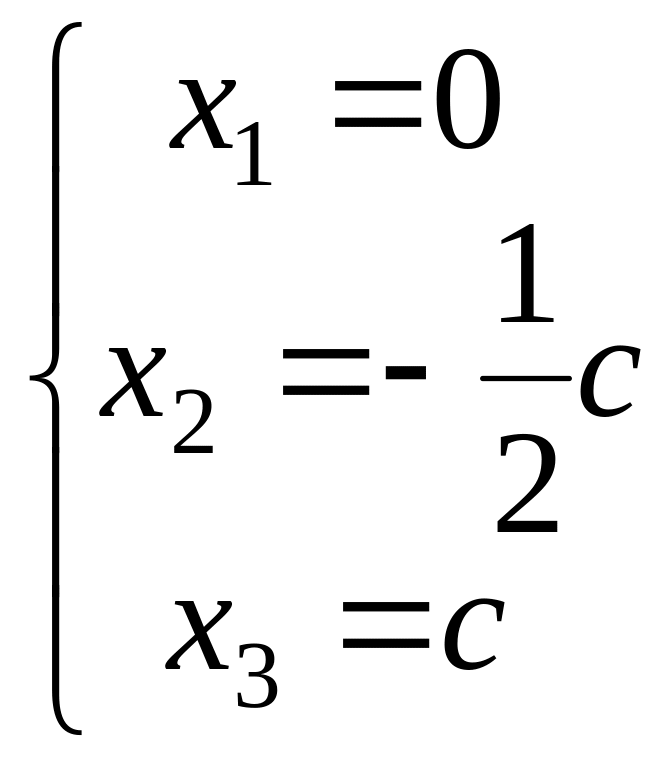и потому получим
При
=
приходим к системе
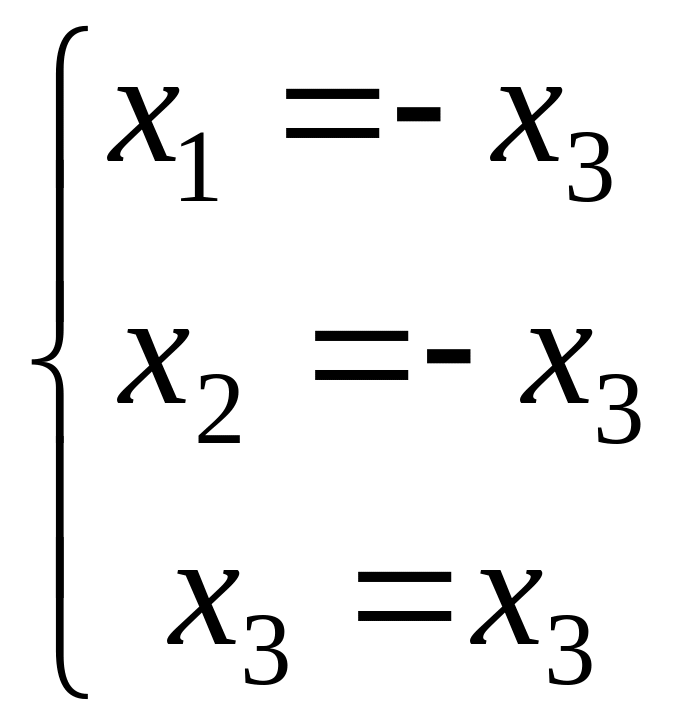
Зададим
,
откуда
,
,
и потому
=
.
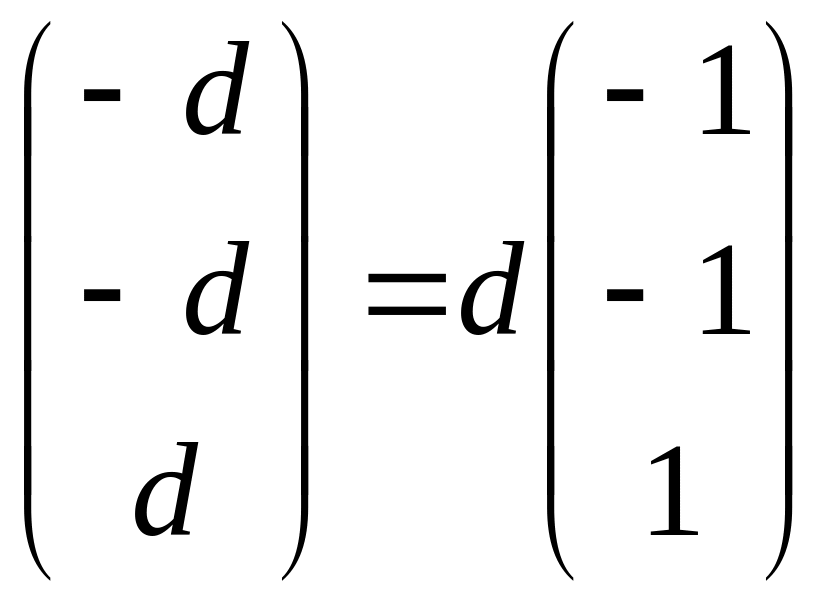
Так как с и d - произвольные числа, то можно положить с = 2 и d=-1, тогда
=
.
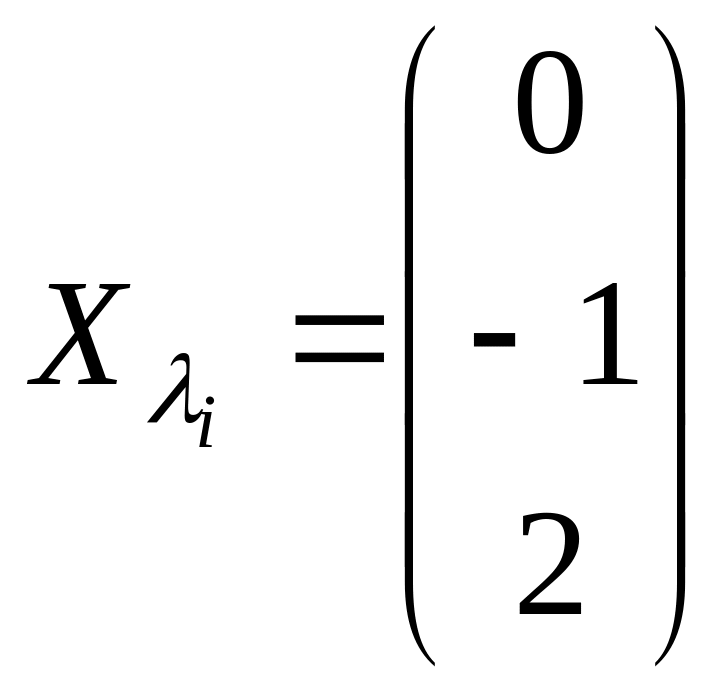
Замечание
1.
С помощью матрицы
,
столбцами которой являются собственные
векторы матрицы
,
матрица
может быть в случае, когда
,
приведена к диагональному виду:
,
где
,
,
.
Пример.
,
,
.
Тогда
,
,
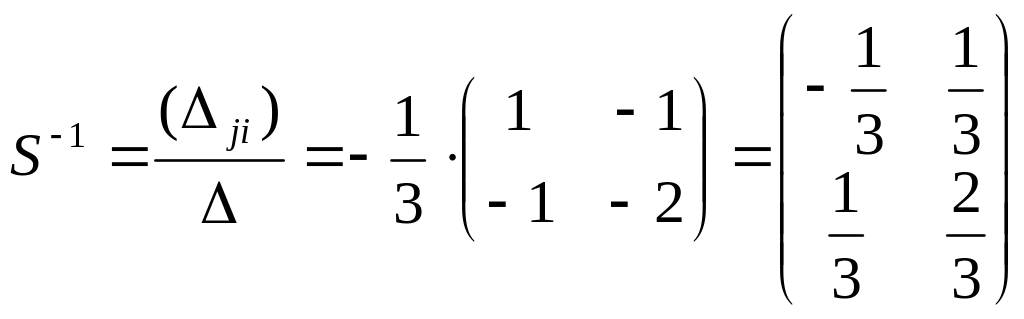
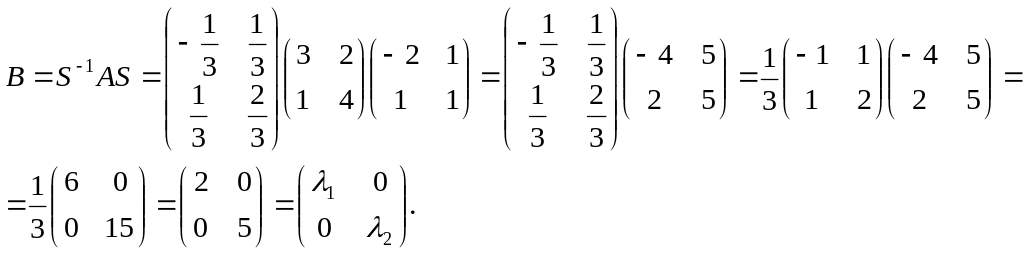
Замечание
2.
Если S
- симметрическая матрица, то матрица
является ортогональной, так как
.
Упражнение.
- симметрическая матрица. Найти
ортогональную матрицу
.
§5. Образцы решения контрольных работ.
Задание №1
Вычислить А2 - 3АВ , где
А
= 
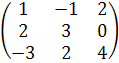В
= 
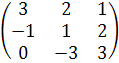
Решение.
А2 = А∙А = ∙ =
(Для получения элемента , стоящего в первой строке и в первом столбце, матрицы А2перемножим соответствующие элементы первой строки матрицы А и элементы первого столбца этой матрицы, т.е первый элемент первой строки матрицы А умножим на первый элемент первого столбца матрицы А ; второй элемент первой строки матрицы А на второй элемент первого столбца этой матрицы ; третий элемент первой строки матрицы А умножим на третий элемент первого столбца матрицы , и их произведения сложим;
для получения элемента , стоящего в первой строке и во втором столбце, перемножим соответствующие элементы первой строки матрицы А и элементы второго столбца матрицы А и их произведения сложим и т.д. )=
= 
= 
= 
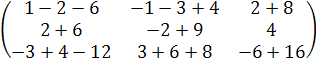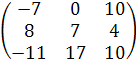
Аналогичным способом находим произведение матриц А и В:
А∙В
= 
∙
=
=
= 
= 
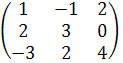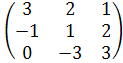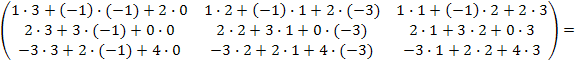
Затем находим
3∙А∙В
= 3∙
=(чтобы
умножить матрицу на число надо каждый
элемент матрицы умножить на это
число)=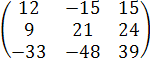
.
Тогда А2 - 3АВ = - =(чтобы вычесть две матрицы, надо вычесть их соответствующие элементы)=
=
.
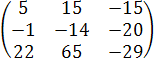Задание №2
Решить систему уравнений
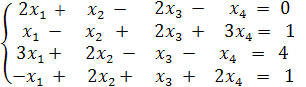(1)
методом Гаусса;
по правилу Крамера;
матричным способом.
Решение.
Метод Гаусса.
Составим расширенную матрицу, соответствующую системе (1) и приведем ее к треугольному виду. Для этого запишем расширенную матрицу данной системы:
и приведем эту матрицу к треугольному виду с помощью элементарнях преобразований, а именно:
- перестановкой строк;
- умножением элементов строки матрицы на число;
- сложение соответствующих (стоящих на одинаковых местах) элементов двух строк и помещение сумм этих элементов на место соответствующих элементов одной из складываемых строк.
Чтобы привести
матрицу к треугольному виду надо получить
нули на месте элементов , стоящих под
главной диагональю.
Сперва
получим нули в первом столбце во второй,
третьей и четвертой строках, т.е. надо
изменить
вторую,третью,четвертую
строки. Так как первая строка не
изменяется, изменения в других строках
будем производить относительно нее:
выберем на главной диагонали неизменяемой
строки главный элемент , в нашем примере
это 2. Если в столбце, в котором мы хотим
получить нули, имеется 1, то для облегчения
счета, строку
с 1
на первом месте лучше поставить
на место первой расширенной матрицы и
сделать ее, тем самым, неизменяемой.В
нашем примере вторая строка содержит
на первом месте 1. Поменяем ее с первой
строкой. Эту операцию обозначим следующим
образом:С
2
С1
,здесь С2
– вторая строка, С1
– первая строка, при этом получим
эквивалентную матрицу
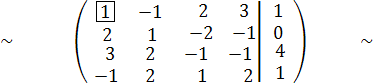
Теперь главным элементом будет 1.Обведем его в квадрат.Чтобы получить на месте 2 во второй строке 0, надо каждый элмент первой строки умножить на (-2) и сложить с соответствующим элементом второй строки и их сумму записать на место соответствующего элемента второй строки. Эту операцию обозначим следующим образом:
С2 := -2∙С1 + С2,
здесь := - это оператор присваивания, т.е. значение выражения с правой стороны записывается на место величины, стоящей слева. Получим при этом эквивалентную матрицу
Чтобы получить вместо 3 в третьей строке нуль, проделаем операцию
С3 := -3∙С1 + С3,
а чтобы получить вместо (-1) в четвертой строке нуль, проделаем операцию
С4 := С1 + С4.
В результате получим эквивалентную матрицу
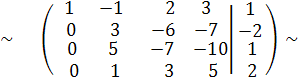
Теперь нужно получить нули во втором столбце в строках три и четыре, т.е. изменяемыми будут третья и четвертая строки. Выберем главный элемент в неизменяемой строке во втором столбце и который стоит на диагонали ( в примере это 3), но среди изменяемых строк имеется строка, в которой во втором столбце стоит 1, поменяем ее со строкой , в которой мы выбрали главный элемент (т.е. надо поменять местами вторую и четвертую строчки)
С
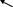4
С2
,
при этом получим эквивалентную матрицу
Теперь главным элементом будет 1. Заключим его в квадрат.Чтобы получить вместо 5 число нуль, проделаем операцию
С3 := -5∙С2 + С3,
а чтобы получить вместо 3 нуль, проделаем операцию
С4 := -3С2 + С4,
при этом получим эквивалентную матрицу
Осталось получить нуль в третьем столбце четвертой строки. Главный элемент выбераем в третьем столбце на диагонали (это -22)(так как изменяемой будет только четвертая строка, и среди изменяемых строк в третьем столбце нет единицы, то -22 и будет главным элементом). Чтобы получить вместо 15 нуль, проделаем следующую операцию
С4 :=- 15∙С3 +22∙ С4,
при этом получим эквивалентную матрицу
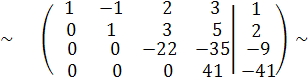
(разделив последнюю строчку полученной матрицы на 41,т.е.С4 := С4 : 41,
получим эквивалентную матрицу)
Запишем по полученной матрице эквивалентную систему уравнений:
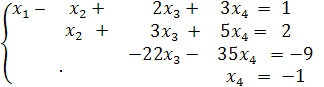
Из последнего уравнения имеем
x4 = -1.
Подставляя это значение в предпоследнее уравнение, получим
- 22x3 - 35∙(-1) =-9. Отсюда находим
Тогда из второго уравнения получим для x2 равенство
x2 +3∙2 + 5∙(-1) = 2 или x2 = 2 – 6 +5 =1.Аналогично,подставляя найденные значения для x2, x3 и x4 в первое уравнение ,получим
x1 - 1 + 2∙2 +3∙(-1) = 1 или x1 = 1.
Ответ: 
.