2. Звуковые волны в газах

Совокупность пространственно-временных распределений величин, характеризующих звук, называется звуковым полем. При достаточно гладкой зависимости характеристик звукового поля (например, при отсутствии скачков давления) задание одной из величин, например давления, полностью определяет все остальные. Для описания звукового поля используются те же математические операции, что и для описания электрических и магнитных полей – градиент и дивергенция (см. работу 2.1).

Звуковые волны в жидкостях и газах в отсутствии внешних сил описываются основными уравнениями гидродинамики и акустики: уравнением непрерывности

, (11.1)

и уравнением Эйлера (для трех компонент вектора скорости )

, (11.2)

где - плотность, - скорость жидкости или газа, - давление в них, основные сведения о дифференциальных операциях дивергенции ( ) и градиенте ( , ) приведены в работе 2.1. Для продольных волн, распространяющихся вдоль прямой (оси Ох)

, , (11.3)

где - единичный вектор вдоль оси Ох, и система уравнений (11.1), (11.2) примет вид

, (11.4)

. (11.5)

Уравнения (11.1), (11.4) являются следствием закона сохранения массы вещества, а уравнения (11.2), (11.5) – следствие второго закона Ньютона. Убедимся в этом на примере звуковых волн, распространяющихся вдоль оси Ох с , , , . Рассмотрим элемент объема в виде куба с ребрами , параллельными осям координат (см. рис. 11.2, подобный рис. 1.5 из работы 2.1).

Рис. 11.2. Применение закона сохранения массы для одномерного течения газа

Объем куба на рис. 11.2 , площадь каждой грани . За время с потоком частиц среды, движущихся со скоростью , через левую грань входит приток массы , а через правую грань выходит отток массы . Изменение массы в объеме куба, равное , представляет собой полный поток вектора плотности потока частиц через поверхность куба. Изменение плотности газа в объеме куба равно

. (11.6)

Напомним (см. работу 2.1), что отношение потока вектора через замкнутую поверхность к объему внутри нее при называется дивергенцией вектора

, (11.7)

где - составляющие вектора , направленные вдоль нормали к граням куба. Скорость изменения плотности со временем равна

,

отсюда и следуют уравнения (11.1), (11.3).

При аналогичном рассмотрении изменения со временем проекции на ось Ох импульса частиц среды, находящихся в объеме куба, получается уравнение (11.5).

Уравнения (11.1), (11.2) дополняются уравнением состояния жидкости или газа, связывающим плотность с давлением

. (11.8)

Система трех уравнений (11.4), (11.5), (11.11) позволяет найти три неизвестные величины: .

Применим уравнения гидродинамики к адиабатическому процессу распространения звука в газе. Уравнением состояния служит адиабата Пуассона¹

, . (11.9)

где и – начальная плотность и начальное давление, и – теплоемкости при постоянном давлении и постоянном объеме.

Относительное изменение плотности газа равное

, (11.10)

называется акустическим сжатием (или конденсацией) газа, при этом плотность газа равна

. (11.11)

Звуковым давлением называется переменная часть давления – отличие от среднего (статического) давления

(11.12)

При малых колебаниях газа и пренебрежении вторыми и высшими степенями относительного изменения плотности , скоростей и градиентов скоростей из уравнений (11.4), (11.5), (11.9), получаются уравнения

, . (11.13)

, (11.14)

. (11.15)

где введено обозначение

. (11.16)

Взаимосвязанная система двух уравнений (11.14), (11.15) для двух функций – акустического сжатия и скорости газа описывает их согласованные колебательные изменения. Подтвердим это с помощью математических преобразований. Дифференцирование первого уравнения (11.14) этой системы по времени , а второго уравнения (11.15) по координате и исключение смешанной второй производной приводит к так называемому волновому уравнению

. (11.17)

В неограниченном пространстве его решениями являются произвольные звуковые волны вида

, , (11.18)

распространяющиеся со скоростью соответственно в положительном и отрицательном направлении оси Ох, где скорость звука¹ дается выражением

. (11.19)

Периодические изменения (возмущения) давления и плотности , распространяющиеся в газах называют звуковыми волнами. Благодаря воздействию возмущений давления на органы слуха (барабанную перепонку уха человека и т.д.) люди и животные чувствуют и различают звуки. Примерами таких волн являются плоские волны, распространяющейся вдоль оси Ох:

, (11.20)

где A – амплитуда,  – циклическая (угловая) частота колебаний, – фаза волны в точках ,  – длина волны, - волновое число

. (11.21)

Скорость звука (11.19) зависит от температуры газа. Действительно, при постоянном давлении

, (11.22)

где - плотность газа при температуре , - абсолютная температура, - масса газа. Для одного моля газа с молярной массой M вследствие уравнения Менделеева-Клапейрона

, (11.23)

где - универсальная газовая постоянная, - объем одного моля, следовательно, скорость звука в газе

. (11.24)

Вследствие уравнения (11.15) скорость одномерного колебательного движения среды связана с давлением формулой

, (11.25)

Результирующий вид звукового поля определяется:

а) волновым уравнением (11.22) в одномерном случае и аналогичным трехмерным уравнением

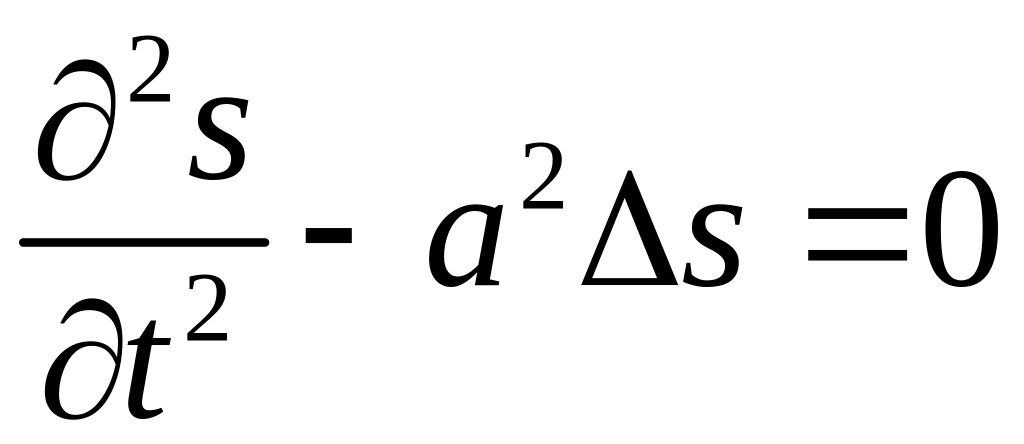. (11.26)

здесь - оператор Лапласа;

б) граничными условиями, например, на абсолютно жесткой границе нормальная компонента колебательной скорости должна обращаться в ноль, на свободной поверхности должно обращаться в ноль звуковое давление ;

в) начальными условиями и внешними воздействиями.