2. Изучение электростатических полей, созданных системой проводящих электродов

Для создания электростатических полей обычно применяется система металлических электродов, часть которых (или все) находятся под определенными потенциалами . Распределение зарядов при этом неизвестно, что не позволяет применить принцип суперпозиции (1.35) для напряженностей электростатического поля. Поэтому необходимо использовать уравнения непосредственно для потенциала . Рассмотрим их для примера плоского (двухмерного) поля, когда

, . (1.12)

Запишем сначала дифференциальное уравнение для напряженности электрического поля. Оно может быть получено из теоремы Гаусса

, (1.13)

для электростатического поля к кубу с ребрами , параллельными осям координат, расположенному вне электродов и электрических зарядов на них (рис. 1.5). Объем куба , площадь грани .

Рис. 1.5. Применение теоремы Гаусса для плоского (двумерного) электрического поля

(1.14)

Отношение потока вектора через поверхность к объему называется дивергенцией вектора . В данном случае

, (1.15)

где – составляющая вектора , направленная вдоль нормали к грани параллелепипеда. Уравнение (1.15) является частным случаем одного из уравнений Максвелла (при отсутствии зарядов)

(1.16)

Из формулы (1.11) следует

. (1.17)

Подстановка последних выражений в уравнение (1.15) приводит к двумерному уравнению Лапласа для потенциала

. (1.18)

Функции, являющиеся решениями уравнения Лапласа¹

. (1.19)

называются гармоническими функциями, они играют важную роль во многих задачах физики и математики.

Для получения единственного решения уравнение Лапласа (1.18) должно быть дополнено граничными условиями. В частности, на поверхности проводящих (металлических) электродов потенциал постоянен и равен поданному на него потенциалу

, (1.20)

где – уравнения линий, описывающих форму электродов. В некоторых случаях задается значение производной по нормали к линии . Например, задается нулевое значение такой производной

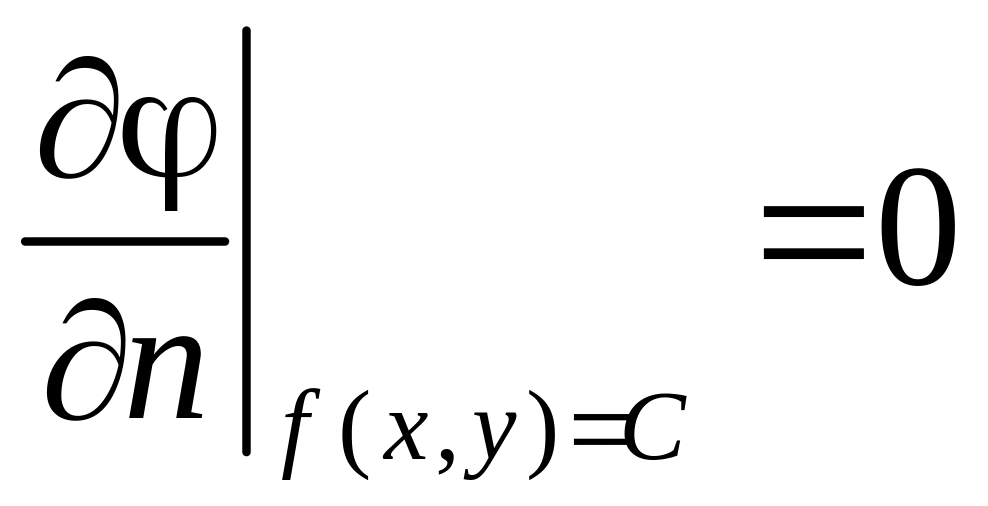. (1.21)

Задачи, подобные (1.18), (1.20), (1.21) называются краевыми задачами. Их аналитическое решение возможно не всегда, поэтому часто приходится применять компьютерные вычисления.

В качестве примера рассмотрим поле, созданное двумя плоскими электродами М и N на токопроводящей бумаге прямоугольной формы. Пусть данному случаю отвечают граничные условия:

на электроде M 0, (1.22)

на электроде N , (1.23)

на краях токопроводящей бумаги . (1.24)

Последнее условие вызвано следующим. Вблизи края токопроводящей бумаги электрический ток, обусловленный направленным движением электронов, направлен параллельно краю. Следовательно, и вектор напряженности электрического поля также направлен параллельно краям листа, а его составляющая, направленная вдоль нормали к краю, равна нулю

. (1.25)

Это условие называют условием отражающего экрана.

Решение уравнения Лапласа (1.18) для двух плоских электродов и граничных условий (1.29)-(1.31)

, (1.26)

линейно зависит лишь от одной переменной. Поэтому его можно представить в виде

, (1.27)

где

(1.28)

Из последнего выражения находится .