6. Работа с компьютерной моделью движения заряда в магнитном поле

Запустите компьютерную программу Открытая физика (версия 2.6) и откройте в Содержании раздел Магнитное поле. 1.18 «Сила Лоренца» Ознакомьтесь с теоретическим материалом, щелкните по изображению модели движения заряда в магнитном поле (рис. 6.7). Рассмотрите движение заряда в магнитном поле при различных значениях скоростей и магнитной индукции. Проанализируйте траектории движения заряда и сделайте выводы.

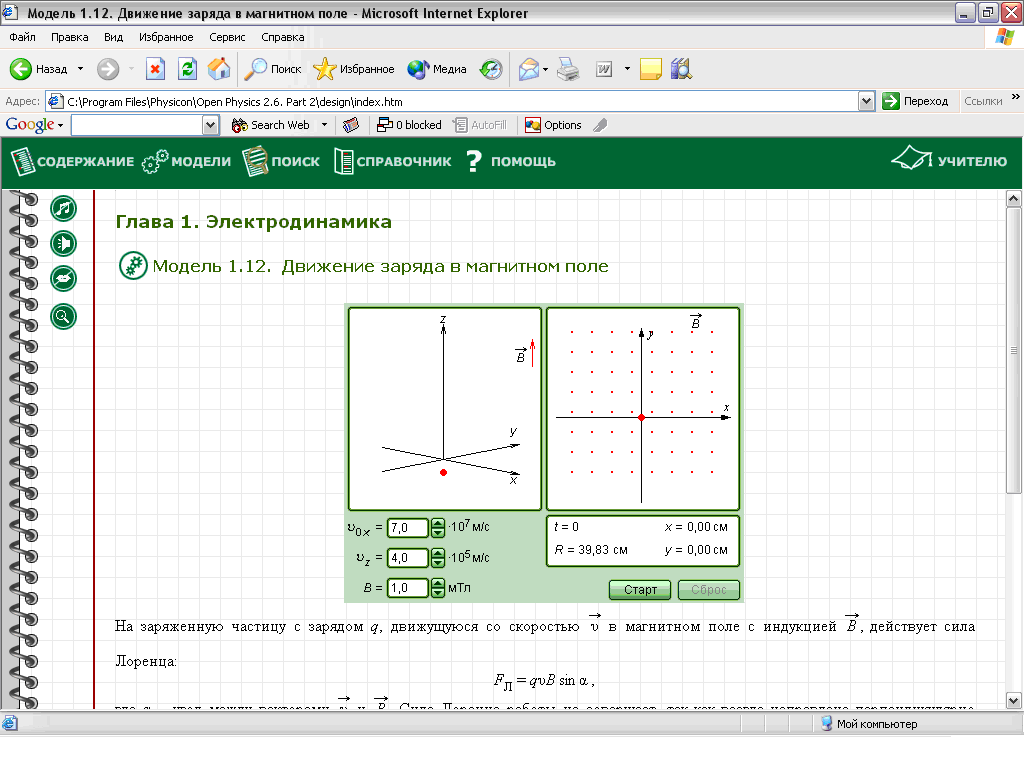
Рис. 6.8. Компьютерная модель движения заряда в магнитном поле.

Контрольные вопросы

1. Дайте определение силы Лоренца. Поясните, как определяется её направление.

1. Расскажите, как движется заряженная частица в электрическом и магнитном полях.

2. Объясните методику измерения удельного заряда электрона. Расскажите, какие упрощающие положения использовались при выводе формулы (6.11).

1. Поясните, какие величины вводят для описания магнитного поля? Какова их связь и единицы измерения в СИ.

Лабораторная работа № 2.7 эффект холла

Цель работы: изучение движения заряженных частиц в электрическом и магнитном полях.

Приборы и принадлежности: датчик Холла (ДХК-050), источники постоянного тока на 17 В и 4,8 В, реостат, амперметр, милливольтметр, миллиамперметр, катушка с обмоткой, постоянный магнит, соединительные провода.

Литература: [1-4]

План работы:

1. Изучение эффекта Холла.

2. Изучение датчиков Холла.

2. Изучение экспериментальной установки.

3. Градуировка датчика.

4. Измерение индукции магнитного поля вдоль оси соленоида.

5. Измерение параметров датчика.

1. Эффект Холла и его теоретическое обоснование

Эффект Холла¹ заключается в возникновении в металле или полупроводнике с током плотностью , помещенном в магнитное поле с индукцией , электрического поля в направлении, перпендикулярном и .

Е сли к электродам 1 и 2 проводника (или полупроводника), имеющего форму прямоугольной пластинки (рис. 7.1) высотой b и толщиной а, приложить напряжение U₁₂, то внутри проводника создастся электрическое поле напряженностью , обуславливающее ток I₁₂ в направлении от электрода 1 к электроду 2.

Э квипотенциальными поверхностями внутри проводника являются плоскости, перпендикулярные к направлению тока. Поэтому разность потенциалов на электродах 3 и 4, находящихся в одной из этих плоскостей, будет равна нулю.

При не эквипотенциальном расположении холловских электродов на выходе датчика Холла появляется «паразитное» напряжение, которое определяется законом Ома. В случае однородной прямоугольной пластины, удельное сопротивление которой не зависит от температуры, это напряжение, называемое резистивным остаточным напряжением, можно представить в виде зависимости U₀=r₀I₁₂, где r₀ – коэффициент резистивного остаточного напряжения, характеризующий величину сопротивления материала, заключенного между эквипотенциальными поверхностями, на которых располагаются холловские электроды.

Если поместить проводник с током между электродами 1 и 2 в магнитное поле, силовые линии которого перпендикулярны плотности тока, то на подвижные заряды будет действовать сила Лоренца , где q – заряд носителей тока, v – скорость упорядоченного движения зарядов под действием продольного электрического поля, направленного от электрода 1 к электроду 2 (см. рис. 7.1).

Если носителями тока являются электроны, то формула для силы Лоренца запишется в виде:

, (7.1)

где e = 1,6·10^-19 Кл – заряд электрона.

Под действием силы электроны, смещаясь к нижней грани пластинки, образуют на ней избыточный отрицательный заряд, на верхней грани появится положительный заряд. Внутри пластинки создается поперечное электрическое поле, напряженностью Сила Лоренца будет уравновешиваться силой поперечного электрического поля. Поэтому

. (7.2)

Таким образом, устанавливается стационарное распределение зарядов в поперечном направлении. Появляющаяся разность потенциалов между электродами 3 и 4 (или Холловская разность потенциалов ), связана с напряженностью электрического поля соотношением

. (7.3)

Известно, что ток

, (7.4)

где j – плотность тока. В соответствии с электронной теорией

(7.5)

где n₀ – концентрация электронов в проводнике.

С учетом формул (7.4) и (7.5) выражение (7.3) примет вид

, (7.6)

где

(7.7)

постоянная Холла.

По измеренному значению постоянной Холла можно определить концентрацию носителей тока в проводнике (при известных характере проводимости и заряде носителей), а так же судить о природе проводимости полупроводников, так как знак постоянной Холла совпадает со знаком заряда носителей тока.

Если в формуле (7.6) обозначить

, (7.8)

где γ называется чувствительностью датчика Холла (ее принято измерять в мВ/Тл), тогда в идеализированном случае

(7.9)

С учетом резистивного остаточного напряжения зависимость от проекции вектора магнитной индукции на нормаль к плоскости датчика оказывается линейной

, . (7.10)

Типичный график зависимости от проекции вектора магнитной индукции на нормаль к плоскости датчика показана на рис. 7.2.

Рис. 7.2. Пример зависимости Холловской разности потенциалов от проекции вектора магнитной индукции на нормаль к плоскости датчика : точки – экспериментальные данные, прямая – результат сглаживания.

Значение постоянной Холла

,

позволяет определить не только концентрацию электронов в проводнике, но и найти среднюю скорость упорядоченного движения электронов. Из формулы (7.5)

или с учетом (7.4)

(7.11)

Если носителями тока являются дырки (см. стр. 17 работы 2.3.), напряжение U₃₄ оказывается противоположным по полярности напряжению Холла в случае электронной проводимости.

Результирующий вектор напряженности электрического поля и ток I при наличии магнитного поля не будут параллельны друг другу. Угол θ между и направлением плотности тока (рис.7.1) получил название угла Холла. В данном случае эквипотенциальные линии, располагаясь перпендикулярно вектору , образуют угол θ с плоскостью, проходящей через электроды 3 и 4.

Принимая во внимание, что и можно рассчитать тангенс угла Холла

(7.12)

Поскольку, согласно (7.8) и (7.9) напряжение U₃₄ прямо пропорционально произведению I₁₂·B, а напряжение U₁₂ прямо пропорционально току I₁₂, то отношение U₃₄/U₁₂, а следовательно и tgθ, будет линейно зависеть от индукции магнитного поля В.