96. Параметрические уравнения прямой и плоскости.

П рямая линия на плоскости или в пространстве полностью определена, когда задана т. , через которую она проходит и направляющий вектор

т. - начальная точка прямой, - направляющий вектор.

97. Параметрические уравнения прямой.

В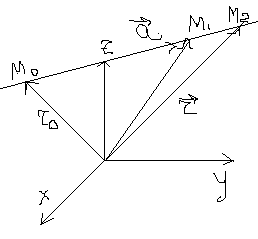 озьмём СК

М- текущая точка на прямой, текущий вектор, по правилу сложения векторов:

- параметрическое уравнение прямой!

t- коэффициент –параметр.

Рассмотрим параметрическое уравнение прямой в координатном виде, тогда получим:

-\

- -- параметрическое уравнение прямой в пространстве (в координатном виде)

- /

-//- на плоскости

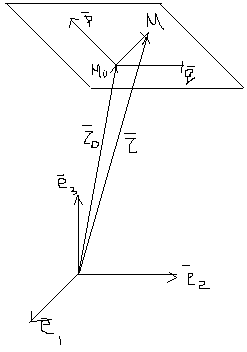
Параметрическое уравнение плоскости в пространстве:

- направляющие векторы, - начальная точка плоскости, М- текущая точка плоскости.

Х= параметрическое уравнение плоскости

Y= в координатном виде

Z=

Рассмотрим связь между общими уравнениями прямой и плоскостью и параметрическими уравнениями:

Общие Ах+Ву+Сz+D=0 – уравнение плоскости

Ах+Ву+С=0 -уравнение прямой

1)Для плоскости:

Ах+Ву+Сz+D=0

таким образом

2)аналогично для прямой

Нахождение координат в начальной точке из общего уравнения:

Рассмотрим как найти направляющие косинусы:

А вычитаем из первого второе

А(х- )+В(у- )=0

Э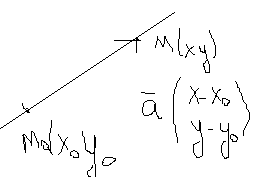 тот вектор параллелен прямой ,когда лежит на этой прямой.

98. Предложение 1. О направляющем векторе прямой на пл-ти.

Каждый не нулевой вектор с компонентыми ,которые удовлетворяют уравнению:

может быть принят за направляющий вектор прямой, определяемый следующим уравнением: Ах+Ву+С=0, в частности направляющий вектор будет

А(х- )+В(у- )= 0

99. Параметрические уравнения плоскости.

А(х- )+В(у- )+С(z- )= 0

100. Предложение 2. О направляющих векторах плоскости.

Любые два неколлинеарных вектора компоненты которых удовлетворяют уравнению:

могут быть приняты за направляющие векторы плоскости в общий декартовой системе координат.

101. Исключение параметра из параметрических уравнений прямой.

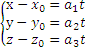параметрические уравнения прямой на плоскости

102. Определение углового коэффициента прямой.

, где к= называется угловым коэффициентом прямой.

Это означает, что точка с координатами (0,в) лежит на прямой.

103. Предложение 3 об уравнении прямой.

Если прямая не параллельная оси координат, то есть , то ее уравнение: у=Кх+В

К-угловой коэффициент, В-точка пересечения с осью У. Из рисунка видно, когда B>0 и когда B<0.

104. Предложение4 об уравнении прямой, параллельной оси ординат.

Если прямая параллельна оси координат, то ее уравнение записывается в виде х= , это получается из параметрического уравнения прямых. Исключим параметр T из параметрических уравнений прямой в пространстве:

105. Каноническое уравнение прямой.

это соответствует тому , что прямая есть пересечение двух плоскостей. Эта прямая лежит в плоскости х= .

106. Векторные уравнения плоскости и прямой.

П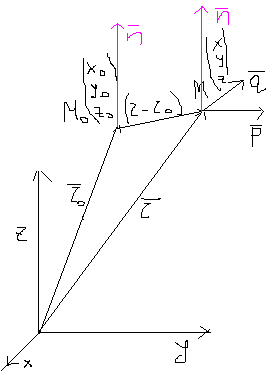 лоскость определяется задание ее начальной точки и вектора этой плоскости.

Условие двух векторов есть скалярное произведение

условие нахождения произведения точки плоскости , то есть векторное уравнение плоскости.

Рассмотрим вектора , тогда в качестве произведению

(( ),[ ])=0 → (( ) )=0 → ( )+D=0 → D= - ( )

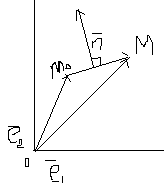
107. Векторные уравнения прямой.

108. Предложение 7.О нормальном векторе прямой на пл-ти.

109. Векторные уравнения прямой в пр-ве.

у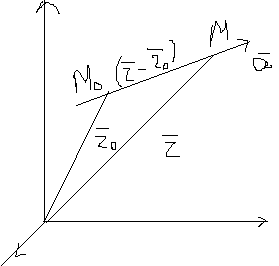 словие коллинеарности:

[( ) ]=0

↑векторное уравнение, направляющий вектор прямой.

Уравнение прямой не содержащее начальную точку:

[ ] = , начальная точка прямой : =t[ ]

110. Векторные уравнения плоскости.

111. Предложение5.О связи векторного и скалярного уравнения плоскости.

Пусть → Ax+By+Cz+D (скалярное произведение) Инаоборот , если имеется такой многочлен, то для него можно найти соответственно.

112. Предложение 6.. О нормальном векторе плоскости.

В ДПСК вектор является нормальным вектором для плоскости, определяемой следующим уравнением: Ах+Ву+Сz+D=0. Всё что мы говорили о плоскостях в пространстве, то же самое мы можем сказать о прямых на плоскости.

прямой

( ), ( )=C

Ax+By+C=0

A=( ) , B=( )

Если в декартовой прямоугольной системе координат вектор

113. Признаки параллельности плоскостей и прямых на плоскости.

в ДСК

Параллельны тогда и только тогда, когда :

а)

условие совпадения:

б) /

из рассмотрения векторного уравнения прямой пересечения.

114. Предложение 8.(О прямых на пл-ти ). Признаки параллельности прямых на плоскости.

115. Предложение 9. ( О плоскостях в пр-ве). Признаки параллельности плоскостей.

116. Предложение 10. (О системе 2-х уравнений).

117. Уравнения прямой в пространстве.

118. Предложение 11. О направляющем векторе прямой в пространстве.

Вектор с компонентами:

= , ,

Н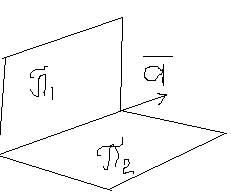 аправляющий вектор прямой, определяемый как пересечение этих двух плоскостей

, =

119. Уравнение прямой, проходящей через две точки.

, , направляющий вектор прямой.

на плоскости

120. Уравнение плоскости, проходящей через три точки.

= 0

Условие комплонарности трех векторов:

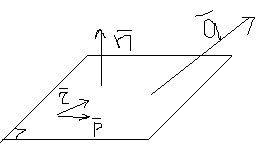
121. Признаки параллельности прямой и плоскости.

Уравнение прямой:

Уравнение плоскости:

( )=0

Направление векторные плоскости:

( )=0 условие параллельности прямой и плоскости:

( )=0

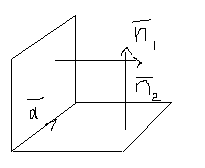Пусть прямая задана пересечением двух плоскостей,

= , ,

Подставим в

Получаем:

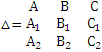= 0

Определитель третьего порядка, вычислим по правилу звездочки.

Три плоскости пересекаются в одной точки тогда и только тогда, когда определитель составленный из их коэффициентов равено нулю.

при 0

122. Уравнения в отрезках плоскости и прямой.

П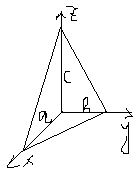 лоскости в пространстве:

+ + -1 = 0

П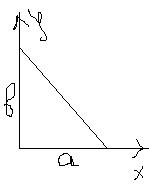 рямой на плоскости:

+ + -1 = 0

123. Предложение1 .О коэффициентах уравнений в отрезках.

Если плоскость задана уравнением общего вида, то числа a,в,c в этом уравнении означают длины отрезков отсекаемых этой плоскостью по осям координат.

Аналогично для прямой.

124. Полупространство. Уравнение п-ва.

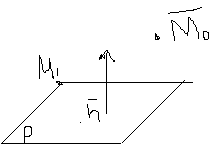
называется нормальным вектором

( )≥0 для верхнего полупространства

( )≤0 для нижнего полупространства

,

Рассмотрим какую-то т. и ее координаты подставим. Если знаки одинаковы,то по одну сторону, если знаки разные, то по разные стороны плоскости.

125. Расстояние от точки до плоскости в векторном виде.

В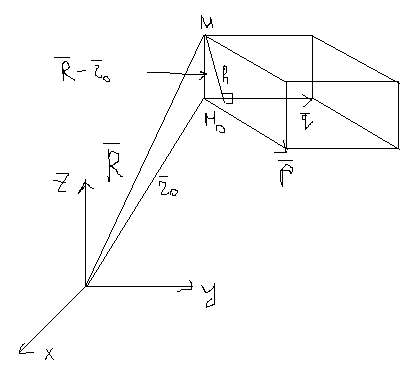 екторы определяют плоскость,

h- расстояние до плоскости

[ ]= Нормированный вектор плоскости

126. Предложение2. Расстояние от точки до плоскости и скалярном виде.

П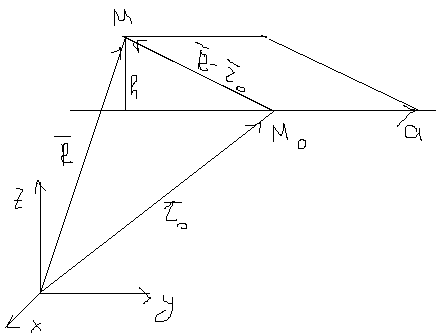 рямая : , М: (x,y,z,)

Построим параллелограмм по векторам и .

Тогда расстояние от точки до прямой будет высота этого параллелограмма:

Имеем формулу для расстояния от точки до прямой

Ах+Ву+С=0 ,

H=

127. Нормированное уравнение пл-ти.

x = 0 направляющий косинус

128. Расстояние от точки до прямой в пр-ве и на пл-ти.

129. Нормированное уравнение прямой на пл-ти.

x = 0 направляющий косинус

130. Расстояние между непараллельными прямыми в пр-ве.

131. Вычисление углов между непараллельными прямыми в пр-ве и на пл-ти.

132. Некоторые задачи на построение.

133. Перпендикуляр из точки на плоскость и на прямую.

134. Проекция точки на прямую и ур-е проекции прямой на пл-ть.

135. Общий Перпендикуляр к 2-м прямым.

Две прямые:

У= х+

У=

tg =

условие перпендикулярности двух прямых на плоскости.

136. Пучок прямых на пл-ти.. Предложение5.

U(x,y)=

V(x,y)=

137. Связка и пучок плоскостей Предложение 6.

U(x,y,z)=

V(x,y,z)=

W(x,y,z)=

Пучок прямых

Связка плоскостей

138. О геометрическом смысле порядка алгебраической линии.

Число точек пересечения алгебраической линии с прямой не может превосходить порядка этой линии:

139. Предложение 7 о пересечении алгебраической линии и прямой.

140-202. Будет спрашивать только то, что дал на консультации.

203. Определители 2-го порядка и системы 2-х уравнений 1-й степени с 2-неизвестными

204. Определители 2-го порядка и Системы 2-х уравнений 1-го степени с 2-мя неизвестными

205. Однородная система двух уравнений первой степени с тремя неизвестными

206. Определители 3-го порядка . Схемы их вычисления.

207. Свойства определителей.. № 1.(Транспонирование).

Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером

2 08. Свойства определителей.. № 2.Перестановка строк или столбцов).

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, равносильна умножению его на -1.т.е.:

209. Свойства определителей.. № 3.(Два одинаковых столбца или строки).

Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

2 10. Свойства определителей.. № 4.(Умножение строки или столбца на число).

Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k.

211. Свойства определителей.. № 5.(Элементы строки или столбца равны).

Определитель матрицы, имеющий два одинаковых ряда, равен нулю. Если элементы к-л столбца, строки =0,то и определитю=0.

212. Свойства определителей.. № 6.(Элементы строки или столбца пропорциональны).

Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю

213. Свойства определителей.. № 7.(Каждый элемент строки или столбца – сумма 2-х слагаемых).

Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.

214. Свойства определителей.. № 8.(Прибавление к элементам строки соответствующих элементов другой строки, умноженных на число).

Алгебраическое дополнение элемента а_ij определителя∆ - определитель Аij=(-1)^i+j М _ij где М_ij - минор элемента а_ij.

По элементам i-й строки:

По элементам j-го столбца:

215. Свойства определителей.. № 9.(Разложение определителей по строке или столбцу).

Определитель n-го порядка, n>1, равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Пример. Вычислим определитель из предыдущего примера разложением по второй строке:

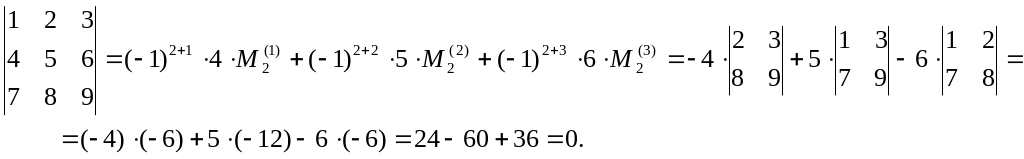Следствие. Определитель треугольной матрицы равен произведению диагональных элементов. (Доказать самостоятельно).

216. Свойства определителей.. № 10.(Сумма произведений элементов строки, умноженных

на число на Алгебраические дополнения другой строки).

217. Алгебраические дополнения и миноры

Минором матрицы порядка r называется определитель, составленный из элементов, расположенных на пересечении любых r строк и r столбцов матрицы;

обозначаем M_r.

Пример.

минор M₂ расположен на пересечении 2-й и 5-й строк с 3-м и 5-м столбцами, а минор M₄ — на пересечении 1-й, 3-й, 4-й и 5-й строк с 1-м, 2-м, 4-м и 5-м столбцами.

Минор M_r, расположенный в первых r строках и в первых r столбцах, называется угловым или главным минором.

218. Решение и исследование системы 3-х уравнений 1-й степени с 3-мя неизвестными – Определитель системы не равен 0.(Правило Крамера). (Получение формулы на основе разложения определителя)

219. Решение и исследование системы 3-х уравнений 1-й степени с 3-мя неизвестными –Δ

системы равен 0, но Δx= Δy= Δz=0.

220. Решение и исследование системы 3-х уравнений 1-й степени с 3-мя неизвестными – Δ

системы равен 0, но Δx= Δy= Δz=0.

221. Сведение произвольной системы 3-х уравнений 1-й степени с 3-мя неизвестными к однородной системе 3-х уравнений 1-й степени с 3-мя неизвестными

222-223. Понятие определителя любого порядка .Перестановки индексов.

224. Формула полного разложения определителя по элементам матрицы.

225. Системы линейных уравнений и их основные свойства.

226. Метод Гаусса решения систем линейных уравнений путем приведения их к треугольному виду.

Метод Гаусса — точный метод решения систем линейных алгебраических уравнений.

Метод Гаусса (его еще называют методом гауссовых исключений) состоит в том, что совместную систему n линейных алгебраических уравнений относительно n неизвестных (определитель матрицы системы отличен от нуля)

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными преобразованиями над строками приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась диагональная матрица

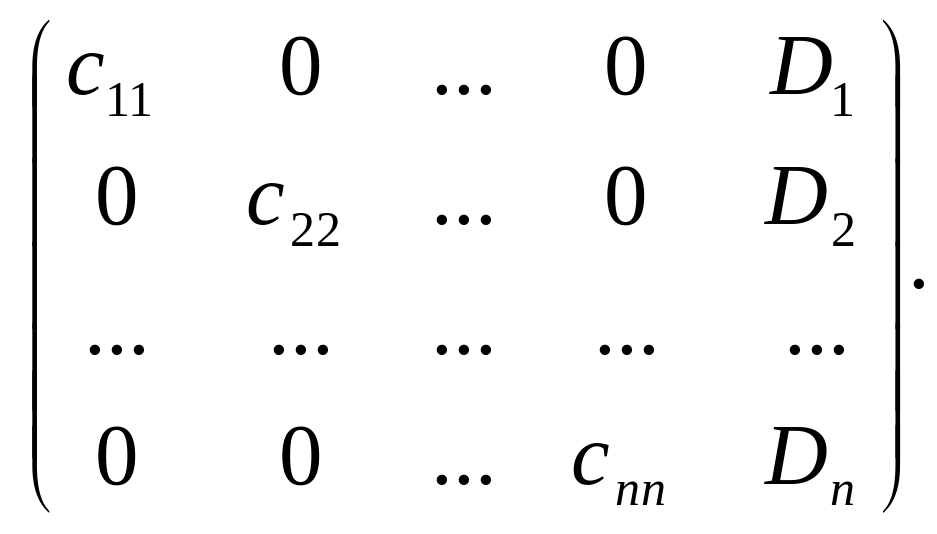
В результате получаем решение системы:

Опишем метод Гаусса последовательно.

Прямой ход

Рассмотрим расширенную матрицу системы

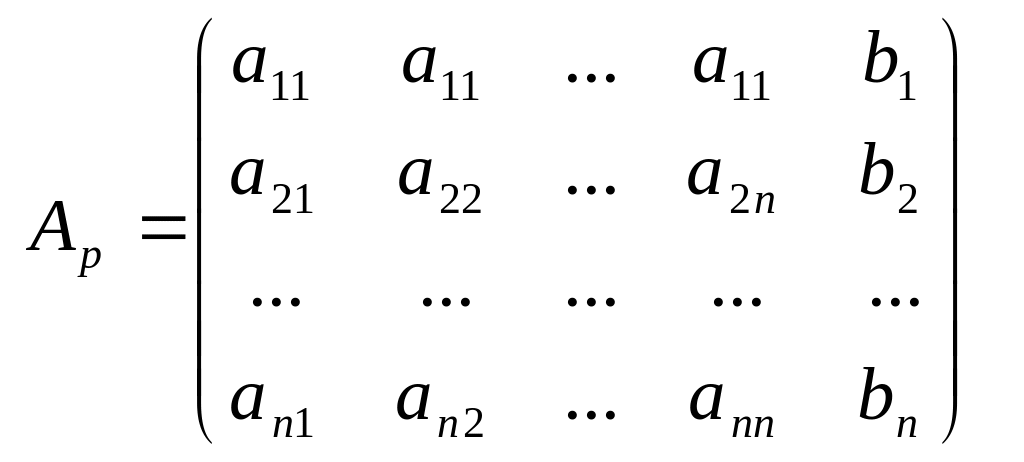
1-й шаг

Предположим, что a₁₁ ≠ 0.

Если это не так, и a₁₁ = 0, переставим строки матрицы так, чтобы a₁₁ ≠ 0. Это всегда возможно, т.к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна.

Элемент a₁₁ ≠ 0 называется ведущим элементом.

Итак, a₁₁ ≠ 0.

Умножим первую строку на число и прибавим ко второй строке,

затем умножим первую строку на число и прибавим к третьей строке, и т.д.,

т.е. последовательно умножаем первую строку на число и прибавляем к i-й строке, для i=2, 3, …, n.

Получим на первом шаге:

.

2-й шаг

Предположим, что a⁽¹⁾₂₂ ≠ 0.

Если это не так, и a⁽¹⁾₂₂ = 0, переставим строки матрицы так, чтобы a⁽¹⁾₂₂ ≠ 0.

Здесь ведущий элемент a₂₂ ≠ 0.

Умножим вторую строку на число 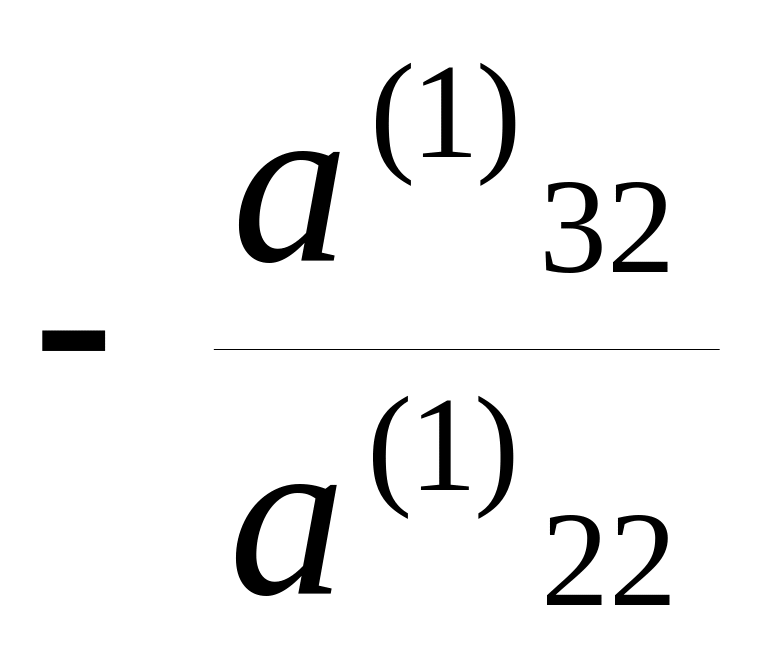и прибавим к третьей строке,

затем умножим вторую строку на число 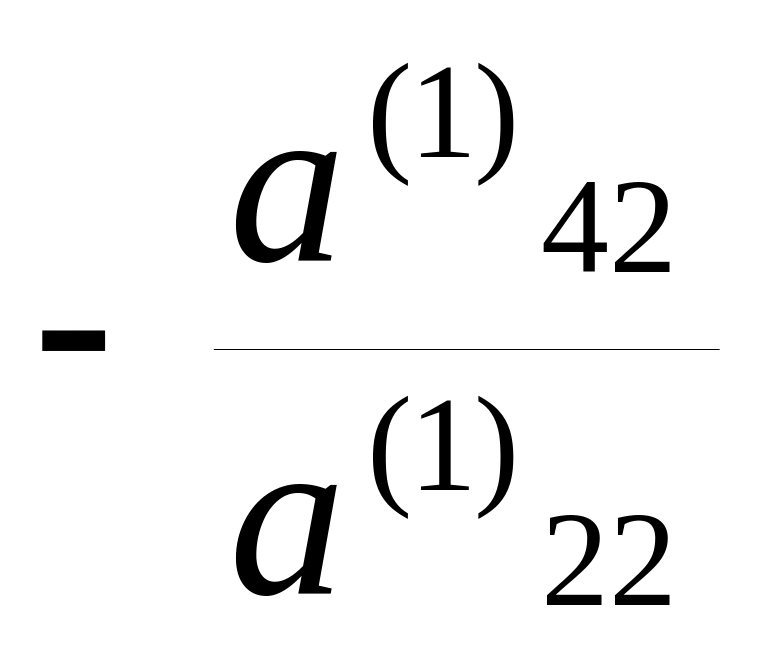и прибавим к четвертой строке, и т.д.,

т.е. последовательно умножаем вторую строку на число 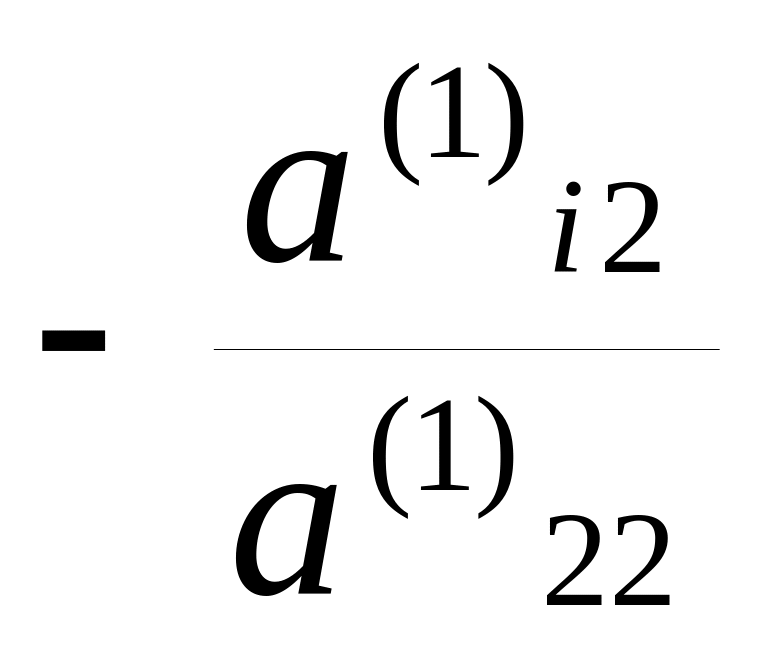и прибавляем к i-й строке, для i=3, 4, …, n.

Получим на втором шаге:

k-й шаг

Предположим, что a^(k-1)_kk≠ 0.

Если это не так, и a^(k-1)_kk = 0, переставим строки матрицы так, чтобы a^(k-1)_kk ≠ 0.

Ведущий элемент a^(k-1)_kk≠ 0.

Умножим k-ю строку на число 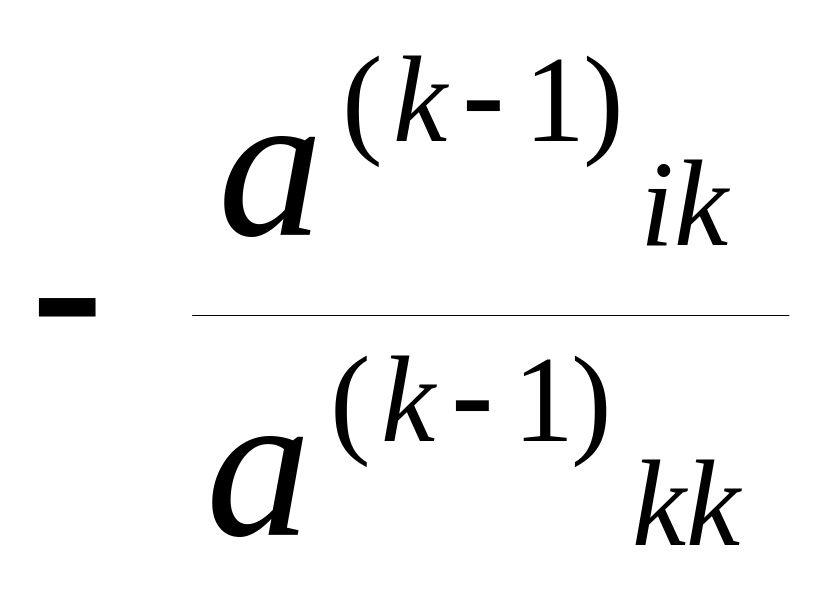и прибавим к i-й строке, для i=k+1, k+2, …, n.

Выполнив n-1 шаг получим:

.

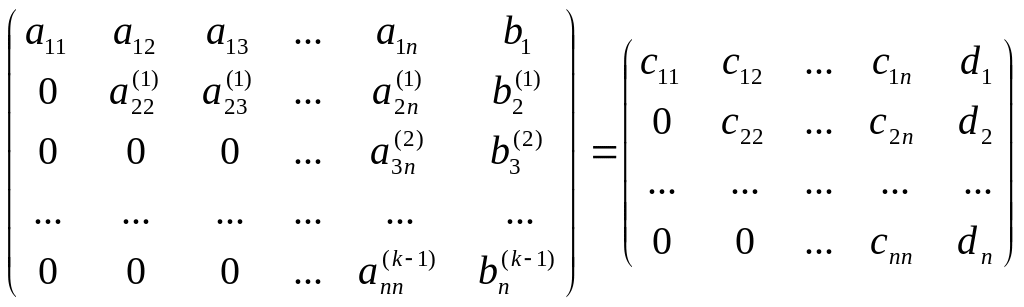Прямой ход закончен. Заметим, что все элементы на главной диагонали отличны от нуля.

Обратный ход

1-й шаг.

Умножим последнюю строку на число и прибавим к предпоследней строке, затем умножим последнюю строку на число и прибавим к (n-2)-й строке, и т.д., т.е. последовательно умножаем последнюю строку на число и прибавляем к (n-i)-й строке, для i=1, 3, …, n-1.

Получим на первом шаге:

.

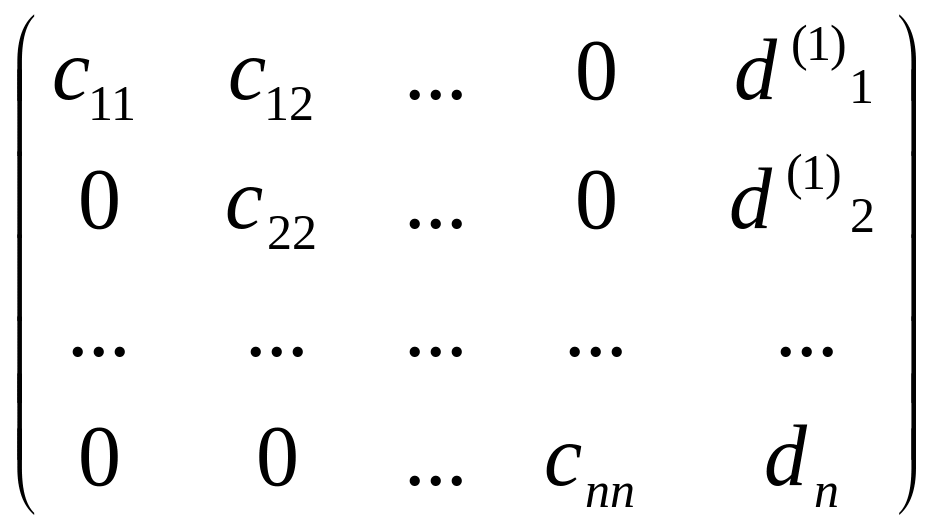k-й шаг

Умножим k-ю строку на число и прибавим к i-й строке, для i=k-1, k-2, …, n­-1.

Выполнив n-1 шаг получим:

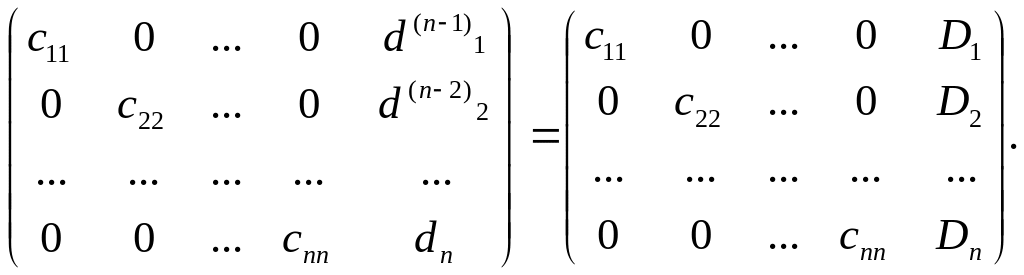
Обратный ход закончен. Решение вычисляем по формулам:

227. Метод Гаусса решения систем линейных уравнений путем приведения их к трапецеидальному виду. (Ранг системы, базисные и свободные переменные, общее и частное решение, фундаментальная система решений)