5.5. Нормальные напряжения при изгибе

Нанесем на боковую поверхность балки, испытывающей чис­тый изгиб (рис. 51, а), продольную линию 00₁ на половине высоты и ряд поперечных параллельных между собой линий. При нагружении двумя противоположно направленными парами сил, действующими в продольной плоскости симметрии (рис. 51, б), балка деформируется - изогнется выпуклостью, вниз. Линии на боковой поверхности балки останутся прямыми, но параллельность их нарушится. Расстояния между концами этих линий на выпуклой стороне увеличатся, а на вогнутой умень­шатся. Расстояния между этими линиями на половине высоты балки останутся такими же, как до деформации. Из этого можно заключить, что при изгибе продольные волокна балки на выпук­лой стороне удлиняются, а на вогнутой укорачиваются; слой волокон, лежащих на половине высоты балки, сохраняет, искри­вившись, неизменную длину нейтральная ось

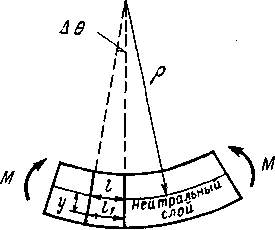
Рис. 51

Рис. 52

Растягивающие и сжимающие напряжения в поперечных сече­ниях балки соответствуют удлинению и укорочению ее продольных волокон. Слой, длина которого не изменяется при изгибе, не испытывает напряжений и называется нейтральным слоем.

Итак, при изгибе поперечные сечения, оставаясь плоскими, поворачиваются одно относительно другого вокруг некоторых осей, лежащих в их плоскостях. Каждое поперечное сечение поворачивается вокруг линии его пересечения с нейтральным слоем. Эта линия называется нейтральной осью поперечного се­чения.

Высказанное положение носит название гипотезы плоских сечений.

Деформации волокон не зависят от положения волокон по ширине балки. Следовательно, нормальные напряжения, изме­няясь по высоте сечения, остаются одинаковыми по ширине балки.

Исходя из этих гипотез, найдем удлинение какого-либо волокна балки при чистом изгибе. Положим, что два близких поперечных сечения балки (рис. 52) повернулись одно относительно другого на угол . Радиус кривизны нейтрального слоя балки, или ее изогнутой оси, обозначим , а длину волокна, лежащего в ней­тральном слое между рассматриваемыми сечениями, -l. Коорди­нату у условимся считать положительной в сторону выпуклости и отрицательной в сторону вогнутости. Удлинение рассматри­ваемого волокна l₁ = l₁ - l, а относительное удлинение (про­дольная деформация)

 = l₁ /l = (l₁ - l)/ l.

Выражая длины дуг l и l₁ через соответствующие радиусы и центральный угол , имеем:

l = ; l₁ = ( + у).

Подставив эти значения, получим

 = [( + у) - у] /() = y/, (38)

т. е. относительные удлинения волокон прямо пропорциональны их расстояниям у от нейтрального слоя.

Зная относительное удлинение, можно применить закон Гука для линейной деформации и выразить нормальное напряжение

 = Е = Е y/. (39)

Эта зависимость определяет линейный закон распределения нормальных напряжений по сечению балки (рис. СОВ). По ширине балки (при определенном у) напряжения постоянны. Наиболь­шего значения нормальные напряжения достигают в точках се­чения, наиболее удаленных от нейтральной оси, причем со стороны выпуклости балки

М

Рис. 53

эти напряжения растягивающие _max, а со стороны вогнутости - сжимающие _min. В точках нейтраль­ной оси х (при у = 0) напряжения равны нулю.

После того как установлен закон распределения нормальных напряжений, в поперечном сечении балки при чистом изгибе, можно перейти к определению напряжений в зависимости от из­гибающего момента в этом сечении. Мысленно рассечем балку некоторым поперечным сечением и выделим в нем произвольную элементарную площадку dA на расстоянии у от нейтральной оси х (рис. 53). Напряжение по этой площадке, согласно формуле (39), составит  = Еy/. Элементарная cила, действующая на площадку,

dN =  dA = (Еy/)dA.

Так как внутренние силы при чистом изгибе приводятся только к изгибающему моменту, то, интегрируя их по сечению, получаем

_A dN = 0; _AdA = 0, (39а)

т.е. сумма проекций внутренних сил на ось балки равна нулю; _A dМ = 0; _AуdA = M, (39б)

т. е. сумма моментов внутренних сил относительно нейтральной оси сечения равна изгибающему моменту.

Рассмотрим первое уравнение равновесия (39а) после под­становки в него значения  = Еy/

_A Еy/ dА = 0; Е/_Aу dA = 0 = Е/S_x, (40)

Входящий в это уравнение интеграл _AуdA = S_x представляет собой статический момент сечения относительно оси х.

Отношение Е/ при изгибе балки не может быть равным нулю, так как E 0 и   0 (ось балки не прямая), поэтому из выра­жения (40) следует, что статический момент сечения относи­тельно оси х должен быть равен нулю. Это будет лишь в случае, если ось проходит через центр тяжести поперечного сечения балки.

Рассмотрим второе уравнение равновесия (39б).

Подставляя значение ст из выражения (39) и вынося постоянные за знак суммы, получаем

Е/_Aу²dA = М.

Входящий в эту формулу интеграл _Aу²dA представляет собой осевой момент инерции J_x поперечного сечения балки относительно нейтральной оси х.

Вводя это обозначение, можем представить последнее выра­жение в виде

Е/ J_x = М,

или

1/ J_x = М/(Е J_x) (41)

Величина, обратная радиусу кривизны в какой-либо точке кривой, называется ее кривизной. Следовательно, формула (41) связывает кривизну нейтрального слоя, а значит кривизну изо­гнутой оси балки, со значением изгибающего момента М и жест­костью сечения балки ЕJ_x относительно нейтральной оси.

Жесткость сечения пропорциональна модулю упругости Е и осевому моменту инерции J_x; иными словами, она определяется материалом, формой и размерами поперечного сечения.

После подстановки полученного для 1/ значения в формулу (41), произведя сокращение, определим нормальное напряжение в любой точке поперечного сечения балки при чистом изгибе

 = Еy/ = Еy М/(Е J_x) = Му/ J_x (42)

Если нейтральная ось сечения совпадает с осью симметрии, то

у_max = 0,5h, где h - высота сечения.

Подставив значения у_шах в формулу для наибольших напряже­ний, получим

 _{max, min} = M0,5h/ J_x = M/( J_x/0,5h).

Отношение осевого момента. инерции к расстоянию до наиболее удаленных от нейтральной оси волокон симметричного сечения называют осевым моментом сопротивления

W_x = (J_x/0,5h). (43)

Наибольшее по абсолютному значению нормальное напряжение в симметричном сечении (растягивающее или сжимающее) может быть определено по формуле

|  |_mах = М/ W_x. (44)

Формула (42) для определения нормальных напряжений вы­ведена для чистого изгиба. Однако ею можно пользоваться и в общем случае прямого поперечного изгиба, когда в сечениях возникает не только изгибающий момент, но и поперечная сила. Поперечные силы, как показывают опыт и теоретические исследо­вания, практически не влияют на нормальные напряжения. Опасным в отношении нормальных напряжений в балках с постоянным сечением будет сечение, в котором изгибающий момент

Рис. 54

имеет наибольшее абсолютное значение.

Упражнение14

1. В каких единицах измеряется осевой момент инер­ции сечения? А. м⁴. Б. м? В. м².

2. Зависят ли значения нормальных напряжений от формы поперечных сечений балки?

А. Зависят. Б. Не зависят.

3. В каких точках поперечного сечения балки возникают наибольшие нор­мальные напряжения (рис. 54)?

А. В точке О. Б. В точке А. В. В точке В.

4.Чему равен осевой момент сопротивления прямоугольника и круга? Указать, для какой точки поперечного сечения балки (рис. 54) нормаль­ные напряжения могут быть вычислены по формуле

 = М/ W_x.

Для точки О. Б. Для точки В. В. Для точек Л и С.