Федеральное агенство по образованию

ГОУ ВПО «Российская экономическая академия имени Г.В. Плеханова»

Кафедра инженерных дисциплин

РУКОВОДСТВО

К ВЫПОЛНЕНИЮ РАСЧЁТНО-ГРАФИЧЕСКИХ РАБОТ

ПО ДИСЦИПЛИНЕ

«ОСНОВЫ ТЕХНИЧЕСКИХ ЗНАНИЙ»

ИЗГИБ БАЛОК, УСТОЙЧИВОСТЬ СТРЕЖНЕЙ

Москва

ГОУ ВПО «РЭА им. Г.В. Плеханова»

2009

Составители: д-р тех. наук А. Е. К у л а г о

д-р тех. наук Е. В. С е м е н о в

А. А. П р о к о п ь е в

канд. физ.-мат. наук Д. А. Т у ш к а н о в

Руководство к выполнению расчётно-графических работ по дисциплине “Основы технических знаний”. Изгиб балок. Устойчивость стержней

/ Сост. А. Е. Кулаго, Е. В. Семёнов, А. А. Прокопьев, Д. А. Тушканов.- М.: ГОУ ВПО «РЭА им. Г.В. Плеханова», 2009. – 51 с.

В работе формулируются исходные положения и количественный аппарат, необходимый студенту для решения задач по расчёту на прочность и устойчивость простейших конструкций.

Для студентов специальности 080502.65 «Экономика и управление на предприятии».

© ГОУ ВПО «РЭА им. Г.В. Плеханова», 2009

Оглавление

5. ИЗГИБ …..……………………………………………………………………. 4

5.1. Основные понятия ………………………………………………………4

5.2. Поперечные силы и изгибающие моменты в сечениях балок………5

5.3. Эпюры поперечных сил и изгибающих моментов……………….......8

5.4. Построение эпюр поперечных сил и изгибающих моментов по характерным точкам……………………………………………………………………………….14

5.5. Нормальные напряжения при изгибе………………………………….18

5.6. Расчеты на прочность при изгибе…………………………………….….24

6. СЛОЖНЫЕ ВИДЫ ДЕФОРМИРУЕМОГО СОСТОЯНИЯ…………………….28

6.1. Понятие о сложном деформированном состоянии…………………28

6.2. Понятие о теориях прочности…………………………………………..….29

6.3. Пример расчета вала на совместное действие изгиба и кручения…..….32

7. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ………………………………..….36

7.1. Понятие о продольном изгибе ………………………………………….….36

7.2. Предел применимости формула Эйлера. ……………………………….…..38

ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ (РГР)…………………………….. ….41

ОТВЕТЫ И КОНСУЛЬТАЦИИ К УПРАЖНЕНИЯМ………………………..….44

СПИСОК ЛИТЕРАТУРЫ…………………………………… ….46

5. Изгиб

5.1. Основные понятия

Элементы конструкций, работающих на изгиб, называют бал­ками. Чаще всего встречается поперечный изгиб, когда внешние силы, перпендикулярные к продольной оси балки, действуют в плоскости, проходящей через ось балки и одну из главных цен­тральных осей ее поперечного сечения, в частности, в плоскости, совпадающей с плоскостью симметрии балки, например, сила F на рис. 37, а. Такой изгиб называют прямым. Если же силы, вы­зывающие деформацию изгиба, действуют в плоскости, проходя­щей через ось балки, но не проходящей через одну из главных центральных осей ее поперечного сечения, имеет место косой изгиб (рис. 37, б).

Рис.37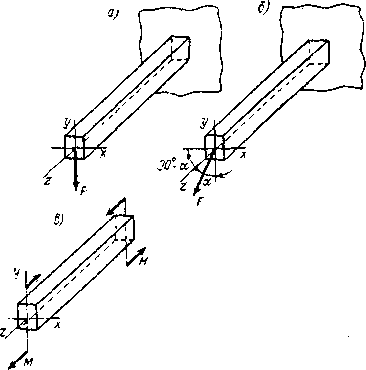

В поперечных сече­ниях балок при изгибе возникают два внутрен­них силовых фактора; изгибающий момент и поперечная сила. Одна­ко возможен такой част­ный случай, когда в по­перечных сечениях бал­ки возникает только один силовой фактор — изгибающий момент, а поперечная сила равна нулю. В этом случае из­гиб называют чистым. Он возникает, в частно­сти, когда балка изги­бается двумя противоположно направленными парами сил, при­ложенными к ее торцам (рис. 35, в). Чистый изгиб возникает при некоторых нагружениях сосредоточенными силами или распределенной нагрузкой.

Упражнение 10

1. В поперечном сечении балки возникли изгибающий момент и поперечная сила. Укажите вид изгиба.

А. Чистый изгиб. Б. Поперечный

Рис. 38

2. Найдите ошибки в приведенных ниже уравнениях равновесия для балки, изображенной на рис. 38:

åМ_А = 0; q×2a× a + F× 3a - R_в× 4а= 0;

åМ_В = 0; - F× a - q× 2a×3a + R_А× 4а = 0;

åF_y = 0; R_А – F + R_в = 0;

5.2. Поперечные силы и изгибающие моменты в сечениях балок

Определим внутренние силовые факторы в сечениях балки АВ (рис. 37, а), на которую действуют сосредоточенные силы F₁, F₂, F₃, перпендикулярные к ее оси. Эти силы вызывают верти­кальные реакции R_A и R_B опор балки. Горизонтальная составляющая реакции

Рис. 39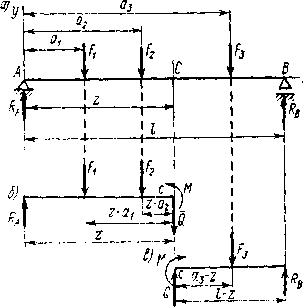

шарнирно-неподвижной опоры при действии только вертикальных сил, перпен­дикулярных к оси балки, очевидно, равна нулю. Опорные реакции R_A и R_B могут быть определены из уравнений равновесия, составлен­ных для всех сил, действующих на балку. Проведем мысленно произ­вольное поперечное сечение С на расстоянии z от левой опоры и рас­смотрим условия равновесия левой и правой отсеченных частей балки (рис. 39, б и в). Левая часть должна находиться в равновесии под действием внешних сил R_A, F₁, F₂ и внутренних сил, возникающих в сечении С. Правая часть должна находиться в равновесии под действием внешних сил F₃, R_B и внутренних сил в проведен­ном сечении С.

Согласно закону равенства действия и противодействия, вну­тренние силы по сечению С для левой и правой частей одинаковы, но направлены в противоположные стороны. Внутренние силы в любом сечении балки могут быть заменены силой Q и парой сил с моментом М. Сила Q называется поперечной силой, а момент М — изгибающим моментом в поперечном сечении балки.

Для сил, действующих на левую отсеченную часть балки (рис. 39, б), составим уравнение равновесия. Уравнение проекций на вертикальную ось у (рис. 39, б);

åF_y = 0; R_А - F₁ - F₂ - Q = 0;

уравнение моментов относительно точки С:

åМ_с = 0; R_A z - F₁  (z - a₁) - F₂  (z - a₂) - М = 0.

Решив первое из этих уравнений относительно Q, а второе относительно М, получим

Q = R_А – F₁ – F₂;

М= R_Az - F₁ (z – a₁) - F₂ (z – a₂).

Итак, поперечная сила и изгибающий момент в любом попереч­ном сечении балки могут быть определены по известным внешним силам, действующим на балку.

Поперечная сила в каком-либо поперечном сечении балки численно равна алгебраической сумме проекций на ось у внешних сил, дей­ствующих на балку по одну сторону от рассматриваемого сече­ния, а изгибающий момент — алгебраической сумме моментов сил, взятых относительно центра тяжести сечения.

Поперечная сила Q и момент пары М действуют на сечение левой и правой отсеченных частей балки в противоположных на­правлениях (рис. 39, б). Чтобы при вычислении изгибающего мо­мента М и поперечной силы Q в каком-либо поперечном сечении балки по внешним силам, действующим слева или справа от этого сечения, получить значения, одинаковые не только по значению, но и по знаку, следует установить противоположные правила зна­ков для сил и их моментов слева и справа от сечения.

Установим правило знаков для изгибающих моментов и попе­речных сил.

Когда внешняя сила, расположенная слева от сечения, вращает оставленную часть балки относителыно центра тяжести сечения по ходу часовой стрелки, то изгибающий момент считают положительным (рис.40, а). При противоположном направлении изгибающий момент считают отрицатель­ным (рис. 40, б).

Для нагрузок, расположенных справа от сечения, направления положительного и отрицательного моментов противоположны соответствующим направлениям слева, так как правило знаков для изгибающих моментов связано с характером деформации балки. Изгибающий момент считается положительным, если балка изгибается выпуклостью вниз—растянутые волокна располо­жены снизу (рис. 38, а).

При изгибе выпуклостью вверх, когда растянутые волокна находятся сверху, момент отрицателен (рис. 40, б).

Для поперечной силы знак также связан с характером дефор­мации. Когда внешние силы действуют слева от сечения вверх, а справа — вниз, поперечная сила положительна (рис. 40, в). При противоположном действии внешних сил, т. е. слева от се­чения вниз, а справа — вверх, поперечная сила отрицательная (рис. 40, г).

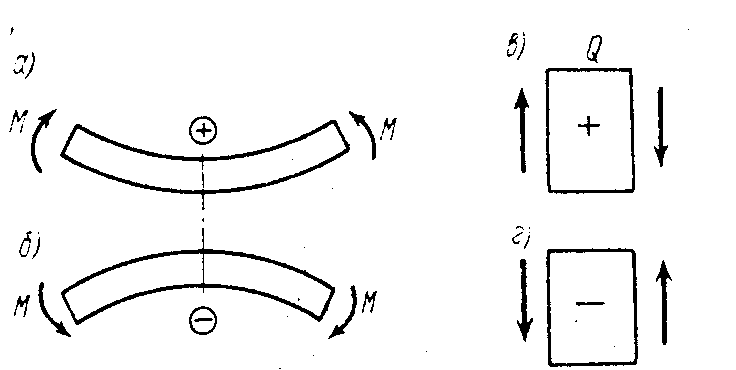
Рис. 40

Внутренние силовые факторы в сечениях балок — поперечная сила Q и изгибающий момент М — зависят от внешней нагрузки и изменяются по длине балки. Законы их изменения представ­ляются некоторыми уравнениями, где аргументами являются координаты z поперечных сечений балки, а функциями — Q или М. Эти уравнения удобно представлять в виде эпюр, ординаты ко­торых для любых значений абсциссы z дают соответствующие значения изгибающего момента М или поперечной силы Q. Эпюры изгибающих моментов и поперечных сил строятся аналогично эпюрам продольных сил (см. 2.1) и крутящих моментов (см. 4.1). При построении эпюр положительные значения поперечных сил и моментов откладывают вверх от оси, отрицательные - вниз;

ось (или базу) эпюры проводят параллельно оси балки.